Codeforces 798C. Mike and gcd problem 模拟构造 数组gcd大于1

C. Mike and gcd problem

time limit per test:

2 seconds

memory limit per test:

256 megabytes

input:

standard input

output:

standard output

Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. .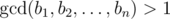

Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbers ai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.

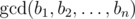 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).

Input

The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

Output

Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.

If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.

Examples

input

2
1 1

output

YES
1

input

3
6 2 4

output

YES
0

input

2
1 3

output

YES
1

Note

In the first example you can simply make one move to obtain sequence [0, 2] with .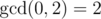

In the second example the gcd of the sequence is already greater than 1.

题目链接：http://codeforces.com/contest/798/problem/C

题意：一次操作中可以选择i (1 ≤ i < n)，删除a_i， a_i + 1添加 a_i - a_i + 1， a_i + a_i + 1到相同的位子。尽可能的操作少的数量使得a数组的最大公约数大于1。注意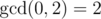

思路：a_i - a_i + 1， a_i + a_i + 1两个数相差2*a_i + 1，2*a_i + 1为它们之间最大公约数的倍数，即它们之间的最大公约数为2*a_i + 1的约数。并且它们的最大公约数不可能为a_i + 1的约数，否则a_i，a_i+1之间的最大公约数大于1，不需要进行操作。那么操作之后的a数组，之间的最大公约数为2。奇偶之间需要2次操作，奇奇之间需要1次操作，偶数直接跳过。

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
const int maxn=1e5+,inf=0x3f3f3f3f,mod=1e9+;
const ll MAXN=1e13+;
int n,a[maxn];
int main()
{
    scanf("%d",&n);
    for(int i=; i<=n; i++) scanf("%d",&a[i]);
    int sign=a[];
    for(int i=; i<=n; i++) sign=__gcd(sign,a[i]);
    if(sign>)
    {
        cout<<"YES"<<endl<<<<endl;
        return ;
    }
    int ans=;
    for(int i=; i<=n; i++) a[i]=a[i]%;
    for(int i=; i<=n; i++)
    {
        if(a[i]==) continue;
        if(i==n) ans+=;
        if(i+<=n)
        {
            if(a[i+]) ans+=;
            else ans+=;
            a[i+]=;
        }
    }
    cout<<"YES"<<endl<<ans<<endl;
    return ;
}

gcd