bzoj4237 稻草人

我是萌萌的传送门

题意不难理解吧……

一开始看到这道题的时候lrd告诉我这题要分治，还给我讲了讲分治要怎么写，好像是CDQ+树状数组来着……(好吧我已经忘了……)然而我第一眼看完题之后的思路是数据结构直接搞，本着“我就不信这个邪了”的念头，就搞出了这么一个树状数组套平衡树维护斜线的奇葩写法。

话说lrd说这题卡常，然而限时40s，我23.8s并没有什么压力，不过运行速度倒数也是感人肺腑……

(我后面就这么几个了……数据结构果然比不上CDQ……QAQ)

言归正传。

如果不用分治的话就需要按照x或者y扫描所有点，并依次处理当前点与之前的点形成的贡献和更新数据结构。

显然对于每个点，对它有贡献的点只能是在它左下角且它的右上角没有其他点的点，如图：

把这些点用线段连起来，可以得到一条斜率始终为负的斜线。如果按照y坐标从小到大处理的话，就可以以y坐标为关键字建立平衡树维护斜线。

每次查询都是前缀查询，直接在平衡树中查询即可。但是会发现一些反例，例如：

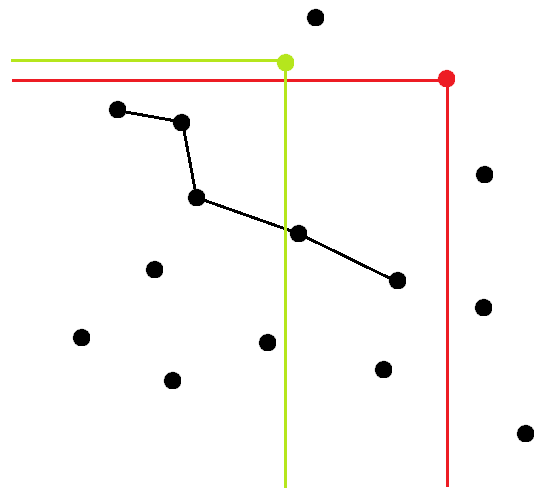
如果先插入红点的话，按照定义应该把斜线清空，只留下红点，然后查询绿点的时候就会WA。

这说明，每插入一个新点就会破坏斜线。也就是说，我们在询问的时候必须只考虑x坐标在当前点左边的点，因为按照y递增处理，只能用一个数据结构维护x。考虑到每个询问都是前缀询问，可以对x离散化后用树状数组维护x坐标，再用平衡树维护位于对应区间内的斜线即可。

查询和更新应该不难想，贴两个图跑算了。

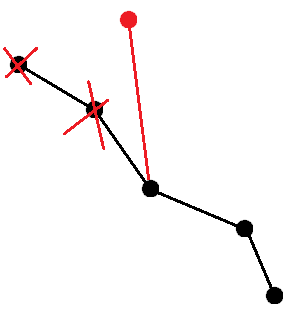
懒得写Treap了，所以用了pb_ds……如果Treap的话还要手写删除所有键值>x的数，有空再说……

 /**************************************************************
     Problem: 4237
     User: hzoier
     Language: C++
     Result: Accepted
     Time:23888 ms
     Memory:70456 kb
 ****************************************************************/

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<ext/pb_ds/assoc_container.hpp>
 #include<ext/pb_ds/tree_policy.hpp>
 using namespace std;
 using namespace __gnu_pbds;
 typedef tree<int,int,less<int>,rb_tree_tag,tree_order_statistics_node_update>rbtree;
 const int maxn=;
 struct A{
     int x,y;
     bool operator<(const A &a)const{return y<a.y;}
 }a[maxn];
 void add(int,int);
 int query(int);
 int n,b[maxn];
 long long ans=;
 rbtree T[maxn];
 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         scanf("%d%d",&a[i].x,&a[i].y);
         b[i]=a[i].x;
     }
     sort(b+,b+n+);
     for(int i=;i<=n;i++)a[i].x=lower_bound(b+,b+n+,a[i].x)-b;
     sort(a+,a+n+);
     for(int i=;i<=n;i++){
         ans+=query(a[i].x);
         add(a[i].x,a[i].y);
     }
     printf("%lld",ans);
     return ;
 }
 void add(int x,int y){
     for(int i=x;i<=n;i+=i&-i){
         rbtree::reverse_iterator it=T[i].rbegin();
         while(it!=T[i].rend()&&it->second<x){
             rbtree::reverse_iterator iter=++it;
             T[i].erase(--it);
             it=iter;
         }
         T[i][y]=x;
     }
 }
 int query(int x){
     int ans=,y=-;
     while(x){
         ans+=T[x].size()-T[x].order_of_key(y);
         if(!T[x].empty())y=max(y,T[x].rbegin()->first);
         x&=x-;
     }
     return ans;
 }

话说这题是一边听教练放歌一边写的，结果费了两节课，这种简单题写这么久，身败名裂……