LOJ6436 [PKUSC2018] 神仙的游戏 【FFT】

题目分析：

题目要求前后缀相同，把串反过来之后是一个很明显的卷积的形式。这样我们可以完成初步判断(即可以知道哪些必然不行)。

然后考虑一下虽然卷积结果成立，但是存在问号冲突的情况。

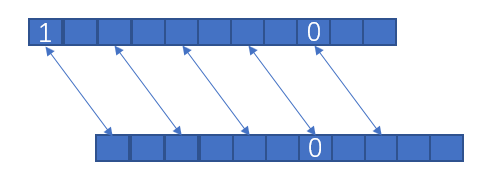
箭头之间应当不存在1。不然就和图上所画的一样。注意到它每隔len个跳一次，所以相当于调和级数，利用原有信息判断即可。

字符串转化的方式有很多种。

代码：

 #include<bits/stdc++.h>
 using namespace std;
 
 const int maxn = (<<)+;
 
 const int mod = ;
 const int gg = ;
 
 char str[maxn];
 
 int n,m,len,a[maxn<<],b[maxn<<],ord[maxn<<];
 
 int f[maxn<<],iv;
 
 int fast_pow(int now,int pw){
     int ans = ,dd = now,bit = ;
     while(bit <= pw){
     if(bit & pw) {ans = (1ll*ans*dd)%mod;}
     dd = (1ll*dd*dd)%mod;
     bit<<=;
     }
     return ans;
 }
 
 void fft(int *d,int dr){
     for(register int i=;i<m;i++) if(i < ord[i]) swap(d[i],d[ord[i]]);
     for(register int i=;i<m;i<<=){
     int wn = fast_pow(gg,(mod-)/(*i));
     if(dr == -) wn = fast_pow(wn,mod-);
     for(register int j=;j<m;j+=(i<<)){
         for(register int k=,w=;k<i;k++,w = (1ll*w*wn)%mod){
         int x = d[j+k],y = (1ll*w*d[j+k+i])%mod;
         d[j+k] = x+y; d[j+k] >=mod?d[j+k]-=mod:;
         d[j+k+i] = x-y;
         d[j+k+i] < ?d[j+k+i]+=mod:;
         }
     }
     }
     if(dr == -){
     for(register int i=;i<m;i++) d[i] = (1ll*d[i]*iv)%mod;
     }
 }
 
 void work(){
     int n = strlen(str);m = ;
     while(m < *n){m<<=;len++;} iv = fast_pow(m,mod-);
     for(register int i=;i<m;i++) ord[i] = (ord[i>>]>>)+((i&)<<len-);
 
     for(register int i=;i<n;i++) {
     if(str[i] == '') a[i] = ;
     else if(str[i] == '') b[n-i-] = ;
     }
 
     fft(a,); fft(b,);
     for(register int i=;i<m;i++) {
     f[i] = (1ll*a[i]*b[i])%mod;
     }
 
     memset(a,,sizeof(a)); memset(b,,sizeof(b));
 
     for(register int i=;i<n;i++) {
     if(str[i] == '') a[i] = ;
     else if(str[i] == '') b[n-i-] = ;
     }
 
     fft(a,); fft(b,);
     for(register int i=;i<m;i++) {
     f[i] += (1ll*a[i]*b[i])%mod; if(f[i] >mod)f[i]-=mod;
     }
 
     fft(f,-);
 
     for(register int i=;i<n-;i++){
     int now = n--i;
     for(register int j=i-now;j>=;j-=now){
         f[i] |= f[j];
     }
     }
 
     long long ans = ;
     for(register int i=;i<=n;i++){
     ans ^= (1ll*(f[i-]==)*i*i);
     }
     printf("%lld",ans);
 }
 
 int main(){
     scanf("%s",str);
     work();
     return ;
 }