SQLServer数据库增删改查

一、数据库定义

数据库(Database)是按照数据结构来组织、存储和管理数据的仓库。数据库的操作分为两种形式：一种是直接在数据库管理工具图形化界面进行操作；一种是使用数据库脚本进行操作，数据库脚本可以直接在数据库管理工具中操作，也可以在dos命令窗口中操作。

二、数据库创建

方式一：数据库图形化管理工具创建数据库步骤：右键点击数据库-》点击新建数据库-》输入数据库名称，可自定义数据库所有者（设置哪些人可以使用数据库）、逻辑名称、初始大小（数据库初始化大小）、自增长大小（数据库新增数据的时候以每次多大存储量增长）、路径（数据库数据文件路径，关系到以后的数据库备份，迁移，还原等操作）、文件名（数据库的文件名称）、日志等属性，左上角的选项和常规可以使用系统默认的-》点击确定即可创建数据库

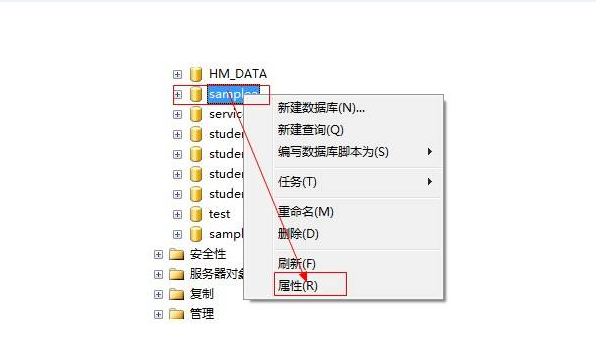
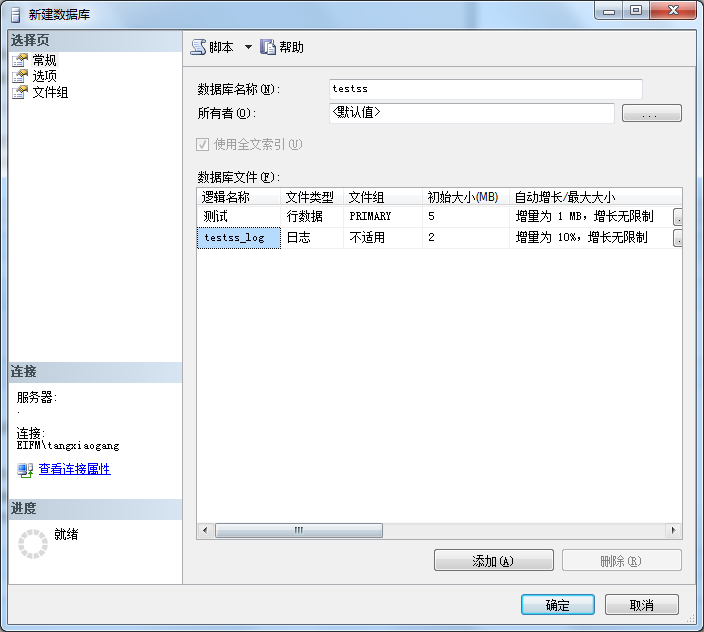
方式二：数据库脚本创建数据库步骤：编写脚本-》在数据库管理工具中执行脚本-》刷新数据库即可显示；

 --创建数据库
 create database testss
 on
 (
     name='testss',
     filename='D:\SqlTest\blog\testss.mdf',
     size=10240kb,
     maxsize=102400kb,
     filegrowth=1024kb
 )
 log on
 (
     name='testlog',
     filename='D:\SqlTest\blog\testlog.ldf',
     size=10240kb,
     maxsize=102400kb,
     filegrowth=1024kb
 )
 go

创建结果示例如下：

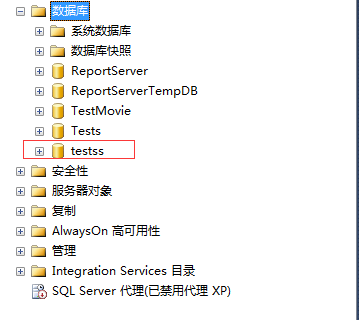
三、数据库删除

方式一：直接在数据库管理工具中右键-》选择删除

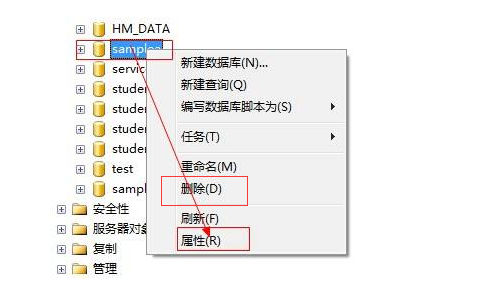
方式二：在数据库管理工具中数据脚本：drop database 数据库名

四、数据库修改

方式一：选中数据库-》右键-》选择重命名-》输入数据库新名称

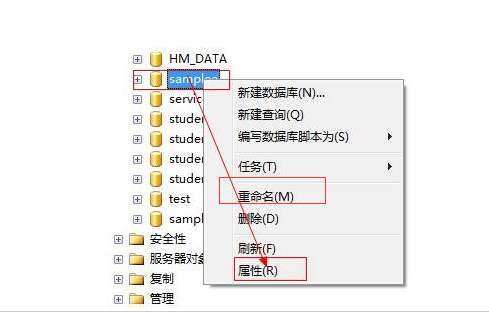
方式二：在数据库管理工具中输入脚本修改：exec sp_renamedb 'testss','test1'或者alter database test1 modify name=test2

五、查数据库查看

方式一：在数据库管理工具中选中数据库-》右键属性-》查看数据库相关配置信息

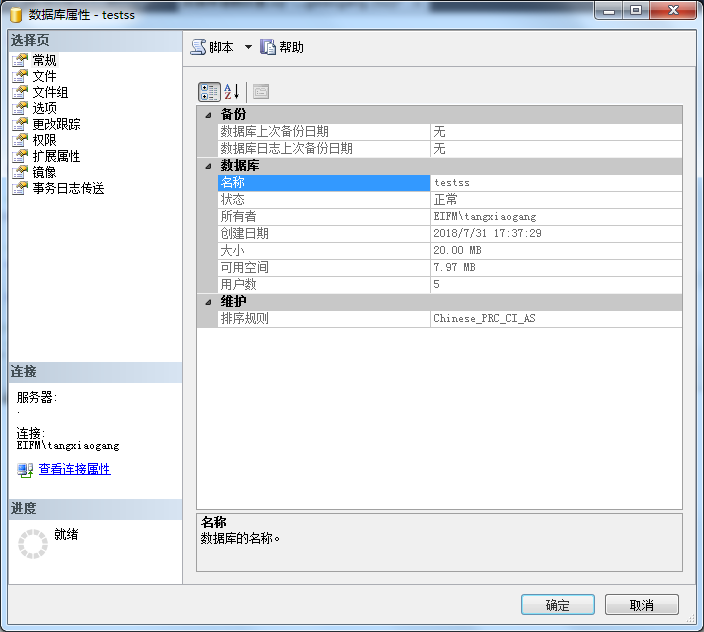
方式二：在数据库管理工具中输入数据库脚本查看，一下列举几种常用的数据库查看信息

--使用目录视图查看数据库信息
--使用sys.database_files查看有关数据库文件的信息
select * from sys.database_files;
--使用sys.filegroups查看有关数据库组的信息
select * from sys.filegroups;
--使用sys.master_files 查看数据库文件的基本信息和状态信息
select * from sys.master_files;
--使用sys.databases 数据库和文件目录视图查看有关数据库的基本信息
select * from sys.databases where name='testss';

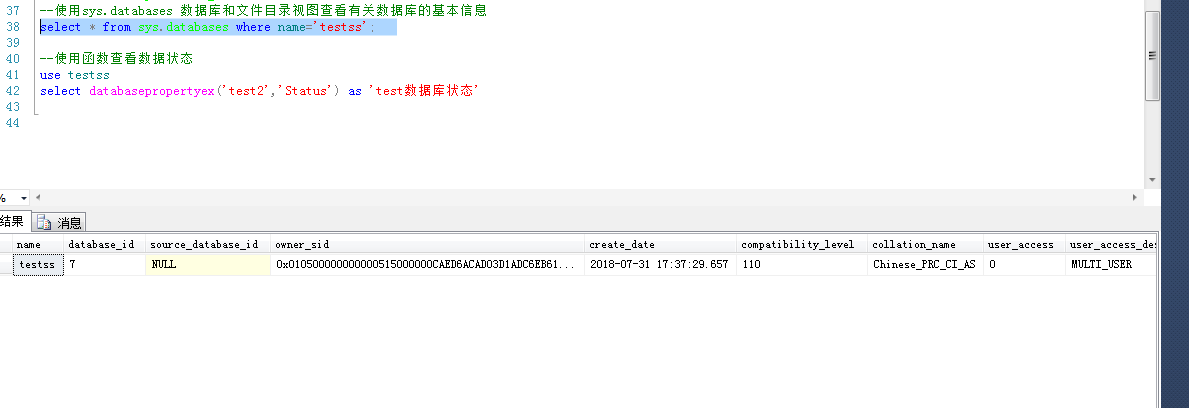
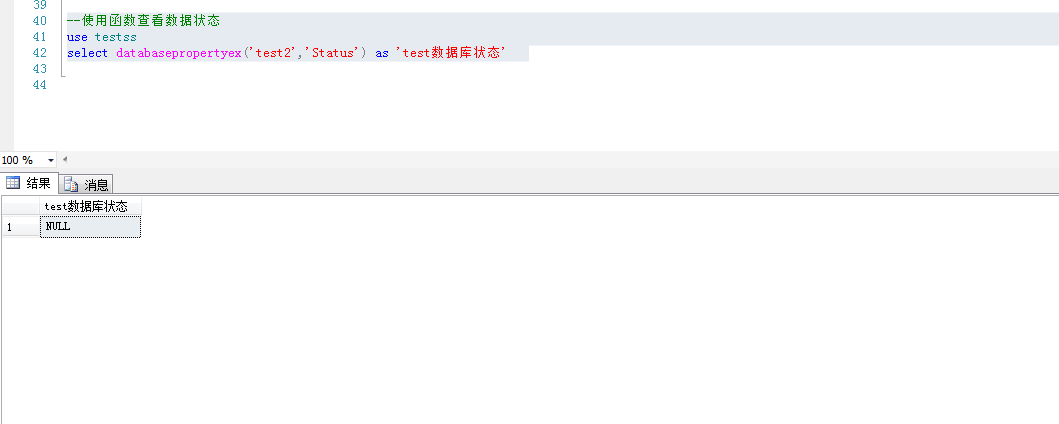
--使用函数查看数据状态
use testss
select databasepropertyex('test2','Status') as 'test数据库状态'

六、数据库优缺点

优点：易用性、适合分布式组织的可伸缩性、用于决策支持的数据仓库功能、与许多其他服务器软件紧密关联的集成性、良好的性价比等。

缺点：1开放性。只能运行在微软的windows平台，没有丝毫的开放性可言。

　　    2可伸缩性，并行性。并行实施和共存模型并不成熟，很难处理日益增多的用户数和数据卷，伸缩性有限。
　　    3性能稳定性。SQLServer当用户连接多时性能会变的很差，并且不够稳定。
　　    4使用风险。SQLServer完全重写的代码，经历了长期的测试，不断延迟，许多功能需时间来证明。并不十分兼容早期产品。使用需要冒一定风险。
　　    5客户端支持及应用模式。只支持C/S模式。