【B2B】01-BFS

纠正我对 01-BFS 问题的错误认识。

我一直以为对于 01-BFS，每次点 $u$ 出队时，对于 $u$ 的邻接边表中的边，只要先松弛边权为 0 的边再松弛边权为 1 的边就能保证每个点只入队一次。最近我发现我错了，例子：



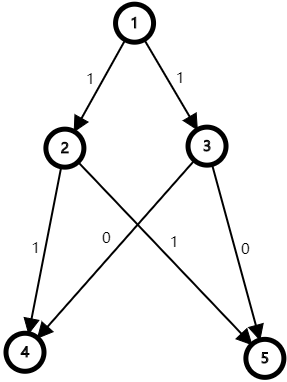
按照上述做法，入队序列是 1, 2, 3, 4, 5, 4, 5。4、5 这两个点入队两次。

一个自然的想法是用一个布尔数组来标记每个点当前是否在队列中以避免重复入队，然而这是行不通的。



出入队序列是

+1, -1, +2, +3, -2, +4, +5, -3, -4, -5, +4, -4

可见 4 号点入队了两次。

01-BFS 的正确做法是用双端队列代替普通队列。每次点 $u$ 出队时，对于 $u$ 的邻接边表中的能够被松弛的有向边 $(u, v)$，若 $(u,v)$ 权值是 0，则将 $v$ 放到队首，否则将 $v$ 放到队尾。当 $(u, v)$ 权值是 0 时，将 $v$ 放到队首相当于把 $v$ 提到了 $u$ 所在的那一层，或者说把 $u$ 和 $v$ 缩成一个点。

代码：

const int max_n = 5000;
vector<int> dis(max_n, INT_MAX);
vector<pair<int,int>> g(max_n);

void bfs(int s) {
    dis[s] = 0;
    deque<int> que;
    que.push(s);
    while (!que.empty()) {
        auto u = que.front();
        que.pop_front();
        for (auto& e, g[u]) {
            if (dis[u] + e.second < dis[e.first]) {
                dis[e.first] = dis[u] + e.second;
                if (e.second == 0) {
                    que.push_front(e.first);
                } else {
                    que.push_back(e.first);
                }
            }
        }
    }
}