一些特殊的矩阵快速幂 hdu5950 hdu3369 hdu 3483

思想启发来自，

罗博士的根据递推公式构造系数矩阵用于快速幂

对于矩阵乘法和矩阵快速幂就不多重复了，网上很多博客都有讲解。主要来学习一下系数矩阵的构造

一开始，最一般的矩阵快速幂，要斐波那契数列Fn=F_n-1+F_n-2的第n项,想必都知道可以构造矩阵来转移

其中，前面那个矩阵就叫做系数矩阵（我比较喜欢叫转移矩阵）

POJ3070 Fibonacci 可以试一试

 #include<cstdio>
 typedef long long ll;
 const ll md=;
 struct Mar{
     int r,c;
     ll a[][];
     Mar(){}
     Mar(int r,int c):r(r),c(c){
         for(int i=;i<r;i++)
             for(int j=;j<c;j++) a[i][j]=;
     }
 }A,T;
 Mar mul(Mar A,Mar B){
     Mar ans(A.r,B.c);
     for(int i=;i<A.r;i++)
         for(int j=;j<B.c;j++)
             for(int k=;k<A.c;k++){
                 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md;
                 if(ans.a[i][j]>=md) ans.a[i][j]-=md;
             }
     return ans;
 }
 Mar poww(Mar A,int b){
     Mar ans(A.r,A.c);
     for(int i=;i<A.r;i++) ans.a[i][i]=;
     while(b){
         if(b&) ans=mul(ans,A);
         A=mul(A,A);
         b>>=;
     }
     return ans;
 }
 void init(ll a,ll b){
     A=Mar(,);
     T=Mar(,);
     A.a[][]=b;A.a[][]=a;
     T.a[][]=T.a[][]=T.a[][]=;
 }
 int main(){
     int t,n;
     ll a,b;
     while(~scanf("%d",&n)&&n!=-){
         if(n==) printf("0\n");
         else{
             init(,);
             T=poww(T,n);
             A=mul(T,A);
             printf("%lld\n",A.a[][]);
         }
     }
     return ;
 }

昭哥说都是水题

然后像类斐波那契数列Fn=a*Fn-1+b*Fn-2 ，也就变一下系数矩阵

而如果是要求斐波那契的前n项和，除去我们知道的第n+2项-1,那对于类斐波那契的前n项和，我们可以设S_n=S_n-1+F_{n，然后构造系数矩阵}

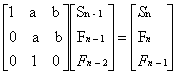
然后对于一些递推公式，转换一下前后几项的关系，也可以构造相应的系数矩阵来矩阵快速幂求解，比如求Σi^x的前n项和的话，设Fn=n^x,Sn=Sn-1+Fn

那么n^x可以写成(n-1+1)^x的形式，把n-1设为a，1设为b，然后就是二项式定理展开了，（二项式展开看右边→_→）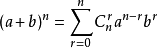

我们就可以得到一个n-1向n转移的递推过程，n^x=C^x_x(n-1)^x+C^x_x(n-1)^x-1+...+C⁰_x (n-1)⁰就可以构造系数矩阵

Recursive sequence HDU - 5950

题意：F1=a,F2=b,Fn=Fn-1+2*Fn-2+n⁴,给出n求Fn

 #include<cstdio>
 typedef long long ll;
 const ll md=;
 struct Mar{
     int r,c;
     ll a[][];
     Mar(){}
     Mar(int r,int c):r(r),c(c){
         for(int i=;i<r;i++)
             for(int j=;j<c;j++) a[i][j]=;
     }
 }A,T;
 Mar mul(Mar A,Mar B){
     Mar ans(A.r,B.c);
     for(int i=;i<A.r;i++)
         for(int j=;j<B.c;j++)
             for(int k=;k<A.c;k++){
                 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md;
                 if(ans.a[i][j]>=md) ans.a[i][j]-=md;
             }
     return ans;
 }
 Mar poww(Mar A,int b){
     Mar ans(A.r,A.c);
     for(int i=;i<A.r;i++) ans.a[i][i]=;
     while(b){
         if(b&) ans=mul(ans,A);
         A=mul(A,A);
         b>>=;
     }
     return ans;
 }
 void init(ll a,ll b){
     A=Mar(,);
     T=Mar(,);
     A.a[][]=b;A.a[][]=a;
     for(int i=,j=;i>=;i--,j<<=) A.a[i][]=j;
     T.a[][]=;T.a[][]=;T.a[][]=;
     for(int i=;i>=;i--){
         T.a[i][]=;
         for(int j=;j>=i;j--)
             T.a[i][j]=T.a[i+][j]+T.a[i+][j+];
     }
     for(int i=;i<;i++) T.a[][i]=T.a[][i];
 }
 int main(){
     int t,n;
     ll a,b;
     scanf("%d",&t);
     while(t--){
         scanf("%d%lld%lld",&n,&a,&b);
         if(n==) printf("%lld\n",a%md);
         else if(n==) printf("%lld\n",b%md);
         else{
             init(a,b);
             T=poww(T,n-);
             A=mul(T,A);
             printf("%lld\n",A.a[][]);
         }
     }
     return ;
 }

+1说这是她去年就懂做的题

那么(an+b)^x的前n项和呢，还是把n写成n-1+1的形式，然后(a(n-1)+1+b)^x二项式分解

(an+b)^x=C^x_x(n-1)^x*a^x*(a+b)⁰+C^x_x(n-1)^x-1*a^x-1*(a+b)¹+...+C⁰_x (n-1)⁰*a⁰*(a+b)^x,然后构造系数矩阵

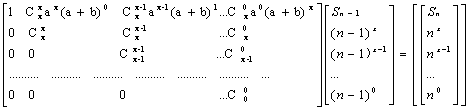
RobotHDU - 3369

题意：有个机器人第n天学n^k个单词，但星期六和星期天休息，不学单词，给出n，k,问机器一共学了多少个单词。

我们已经可以求n^k的前n项和了，那么接下来只需要求出星期六和星期天的再减去，即可。

那么，我们根据开始的星期几到下一个星期六距离的天数x,和下一个星期天距离的天数x+1，

那么要减去的部分就是，(7m1+x)^k 和(7m2+x+1)^k的前m项和m1=(n-x)/7,m2=(n-x-1)/7,且第一项分别是x^k和(x+1)^k

（转移矩阵懒得画了）

 #include<cstdio>
 typedef long long ll;
 const ll md=1e9+;
 struct Mar{
     int r,c;
     ll a[][];
     Mar(){}
     Mar(int r,int c):r(r),c(c){
         for(int i=;i<r;i++)
             for(int j=;j<c;j++) a[i][j]=;
     }
 }A,T;
 char s[];
 ll cf[][];
 Mar mul(Mar A,Mar B){
     Mar ans(A.r,B.c);
     for(int i=;i<A.r;i++)
         for(int j=;j<B.c;j++)
             for(int k=;k<A.c;k++){
                 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md;
                 if(ans.a[i][j]>=md) ans.a[i][j]-=md;
             }
     return ans;
 }
 Mar poww(Mar A,int b){
     Mar ans(A.r,A.c);
     for(int i=;i<A.r;i++) ans.a[i][i]=;
     while(b){
         if(b&) ans=mul(ans,A);
         A=mul(A,A);
         b>>=;
     }
     return ans;
 }
 void init(int n,ll f0,ll a,ll b){
     A=Mar(n,);
     T=Mar(n,n);
     A.a[][]=f0,A.a[n-][]=;
     for(int i=n-;i>=;i--){
         T.a[i][n-]=;
         for(int j=n-;j>=i;j--){
             T.a[i][j]=T.a[i+][j]+T.a[i+][j+];
             if(T.a[i][j]>=md) T.a[i][j]-=md;
         }
     }
     T.a[][]=;
     for(int i=;i<n;i++){
         T.a[][i]=T.a[][i];
         T.a[][i]*=cf[a][n--i];
         if(T.a[][i]>=md) T.a[][i]%=md;
         T.a[][i]*=cf[a+b][i-];
         if(T.a[][i]>=md) T.a[][i]%=md;
     }
 }
 ll solve(int n,int m,int x){
     ll ans1,ans2,ans3;
     init(m+,,,);T=poww(T,n);
     A=mul(T,A);ans1=A.a[][];
     init(m+,cf[x][m],,x);T=poww(T,(n-x)/);
     A=mul(T,A);ans2=A.a[][];
     init(m+,cf[x+][m],,x+);T=poww(T,(n-x-)/);
     A=mul(T,A);ans3=A.a[][];
     return ((((ans1-ans2)%md+md)%md-ans3)%md+md)%md;
 }
 int main(){
     for(int i=;i<=;i++){
         cf[i][]=;
         for(int j=;j<=;j++){
             cf[i][j]=cf[i][j-]*i;
             if(cf[i][j]>=md) cf[i][j]%=md;
         }
     }
     int t=,T,n,m,x;
     scanf("%d",&T);
     while(t<=T){
         scanf("%s",s);
         scanf("%d%d",&n,&m);
         if(s[]=='M') x=;
         else if(s[]=='T'&&s[]=='u') x=;
         else if(s[]=='W') x=;
         else if(s[]=='T') x=;
         else if(s[]=='F') x=;
         else if(s[]=='S'&&s[]=='a') x=;
         else x=;
         ll ans=solve(n,m,x);
         printf("Case %d: %lld\n",t++,ans);
     }
     return ;
 }

我也想学那么多单词

最后，如果是要求n^xxⁿ的前n项和呢，一样把n写成n-1+1，然后(n-1+1)^xxⁿ二项式分解

n^xxⁿ=C^x_x(n-1)^x*x^n-1+1+C^x_x(n-1)^x-1*x^n-1+1+...+C⁰_x (n-1)⁰*x^n-1+1,转移矩阵就有了

A Very Simple ProblemHDU - 3483

求n^xxⁿ的前n项和的模板题

 #include<cstdio>
 typedef long long ll;
 const int N=;
 struct Mar{
     int r,c;
     ll a[N][N];
     Mar(){}
     Mar(int r,int c):r(r),c(c){
         for(int i=;i<r;i++)
             for(int j=;j<c;j++) a[i][j]=;
     }
 }A,T;
 ll md        ;
 Mar mul(Mar A,Mar B){
     Mar ans(A.r,B.c);
     for(int i=;i<A.r;i++)
         for(int j=;j<B.c;j++)
             for(int k=;k<A.c;k++){
                 ans.a[i][j]+=A.a[i][k]*B.a[k][j]%md;
                 if(ans.a[i][j]>=md) ans.a[i][j]-=md;
             }
     return ans;
 }
 Mar poww(Mar A,int b){
     Mar ans(A.r,A.c);
     for(int i=;i<A.r;i++) ans.a[i][i]=;
     while(b){
         if(b&) ans=mul(ans,A);
         A=mul(A,A);
         b>>=;
     }
     return ans;
 }
 void init(int n,int x){
     A=Mar(n,);
     T=Mar(n,n);
     A.a[n-][]=;
     T.a[][]=;
     for(int i=n-;i>=;i--){
         T.a[i][n-]=;
         for(int j=n-;j>=i;j--){
             T.a[i][j]=T.a[i+][j]+T.a[i+][j+];
             if(T.a[i][j]>=md) T.a[i][j]-=md;
         }
     }
     for(int i=n-;i>=;i--)
         for(int j=n-;j>=i;j--){
             T.a[i][j]*=x;
             if(T.a[i][j]>=md) T.a[i][j]%=md;
         }
     for(int i=;i<n;i++) T.a[][i]=T.a[][i];
 }
 int main(){
     int n,x;
     while(~scanf("%d%d%lld",&n,&x,&md)){
         if(n<&&x<&&md<) break;
         init(x+,x);
         T=poww(T,n);
         A=mul(T,A);
         printf("%lld\n",A.a[][]);
     }
     return ;
 }

啊，学到了