Noip2016 提高组 Day2 T1 组合数问题

题目描述

组合数表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3) 三个物品中选择两个物品可以有（1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义，我们可以给出计算组合数的一般公式：

其中n! = 1 × 2 × · · · × n

小葱想知道如果给定n,m和k，对于所有的0 <= i <= n，0 <= j <= min(i,m)有多少对 (i,j)满足是k的倍数。

输入输出格式

输入格式：

第一行有两个整数t,k，其中t代表该测试点总共有多少组测试数据，k的意义见 【问题描述】。

接下来t行每行两个整数n,m，其中n,m的意义见【问题描述】。

输出格式：

t行，每行一个整数代表答案。

输入输出样例

输入样例#1：

1 2
3 3

输出样例#1：

1

输入样例#2：

2 5
4 5
6 7

输出样例#2：

0
7

说明

【样例1说明】

在所有可能的情况中，只有是2的倍数。

【子任务】

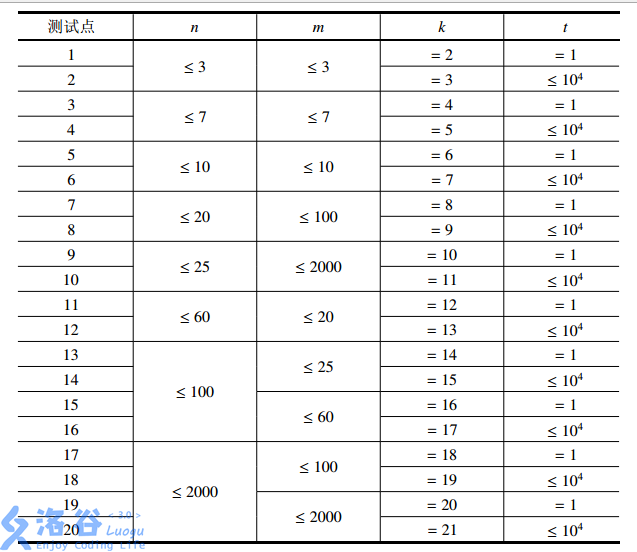
思路:

　　该题需要使用到组合数的递推式

　　　　C[i][j]=(C[i-1][j]%k+C[i-1][j-1]%k)%k(需要在预处理的时候随手取模)

　　解释:n个物品中取m个物品，若不取a这个物品，则从n-1个物体中选m个;

　　　　若取a这个物品则从n-1中选m-1个。

　　　　详见高中数学课本选修2—3

　　然后我们做完上述预处理之后，从头到尾扫一遍C数组是否为0即可知道是否为k的倍数。

　　按要求输出即可，这题就到此结束啦！

　　但是。。这样就真的over了吗?!

　　没有！

　　其实是只有90分的。。。。

　　什么？为何不满分？

　　大概是扫C数组太花时间了吧。。。。所以我们还需要一些优化！

　　我们预处理了C数组，那么是否还可以预处理一下k的倍数的个数？

　　答案是肯定的！

　　令s[i][j]表示在所有的C(i,j) (1≤j≤i)的里面，为k的倍数的有多少个，所以得到处理数组的时候就是p[i][j] = p[i][j-1] ，然后使每找到一个C[i][j]为0就让p[i][j]的值+1。

　　最后只需要从1-n循环一遍令ans+=p[i][j]，最后输出ans即可（注意这里的0 <= j <= min(i,m)！）

　　好啦！这样就ok啦！

上代码:

#include <iostream>
#include <cstdio>
using namespace std;

const int N = ;
const int M = ;
int T,k,n,m,ans;
int C[N][M],p[N][M];

void pre() {
    for(int i=; i<N; ++i) {
        C[i][]=C[i][i]=;
        for(int j=; j<i; ++j)
            C[i][j]=(C[i-][j]%k+C[i-][j-]%k)%k;
    }
    for(int i=; i<N; ++i)
        for(int j=; j<=i; ++j) {
            p[i][j]=p[i][j-];
            if(C[i][j]==)
                p[i][j]++;
        }
}

int main() {
    scanf("%d%d",&T,&k);
    pre();
    while(T--) {
        scanf("%d%d",&n,&m);
        for(int i=,j; i<=n; ++i) {
            j=min(i,m);
            ans+=p[i][j];
        }
        printf("%d\n",ans);
        ans=;
    }
    return ;
}