day39KNN算法和其他的算法

PS:

1.现在明白为什么其他的同学一直都在做数字图像处理，matlab这种东西了，因为机器学习，其他底层主要是做预先处理，然后调用某一个算法

2.感觉knn算法就是根据先验数据计算下一个跟自己一样不一样

1. kNN分类算法原理

1.1 概述

K最近邻（k-Nearest Neighbor，KNN）分类算法是最简单的机器学习算法。

KNN算法的指导思想是“近朱者赤，近墨者黑”，由你的邻居来推断出你的类别。

本质上，KNN算法就是用距离来衡量样本之间的相似度

1.2 算法图示

v 从训练集中找到和新数据最接近的k条记录，然后根据多数类来决定新数据类别。

v 算法涉及3个主要因素：

1) 训练数据集

2) 距离或相似度的计算衡量

3) k的大小

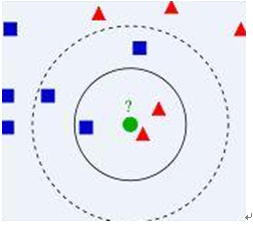
v 算法描述

1) 已知两类“先验”数据，分别是蓝方块和红三角，他们分布在一个二维空间中

2) 有一个未知类别的数据（绿点），需要判断它是属于“蓝方块”还是“红三角”类

3) 考察离绿点最近的3个（或k个）数据点的类别，占多数的类别即为绿点判定类别

1.3 算法要点

1.3.1、计算步骤

计算步骤如下：

1）算距离：给定测试对象，计算它与训练集中的每个对象的距离

2）找邻居：圈定距离最近的k个训练对象，作为测试对象的近邻

3）做分类：根据这k个近邻归属的主要类别，来对测试对象分类

1.3.2、相似度的衡量

v 距离越近应该意味着这两个点属于一个分类的可能性越大。

但，距离不能代表一切，有些数据的相似度衡量并不适合用距离

v 相似度衡量方法：包括欧式距离、夹角余弦等。

（简单应用中，一般使用欧氏距离，但对于文本分类来说，使用余弦(cosine)来计算相似度就比欧式(Euclidean)距离更合适）

1.3.3、类别的判定

v 简单投票法：少数服从多数，近邻中哪个类别的点最多就分为该类。

v 加权投票法：根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）

1.4 算法不足之处

1. 样本不平衡容易导致结果错误

² 如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。

² 改善方法：对此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。

1. 计算量较大

² 因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。

² 改善方法：事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

该方法比较适用于样本容量比较大的类域的分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

------------------------------------------------------------------------------------------------------------------

#coding=utf-8
'''
kNN:k近邻

Input:      inX: 待分类向量 (1xN)
            dataSet: 先验数据集 (NxM)
            labels: 先验数据分类标签 (1xM vector)
            k: 参数：k个近邻 (should be an odd number)

Output:     分类标签

'''
from numpy import *
import operator
from os import listdir

def classify0(inX, dataSet, labels, k): #待验证的点，先验数据，数据的类别，最近的几个紧邻
    dataSetSize = dataSet.shape[0]      #得到先验数据的行数
    diffMat = tile(inX, (dataSetSize,1)) - dataSet  #构造七行数据一模一样，然后减去数据集
    sqDiffMat = diffMat**2        #平方
    sqDistances = sqDiffMat.sum(axis=1)  #按列叠加
    distances = sqDistances**0.5         #开方
    sortedDistIndicies = distances.argsort()     #返回原来位置的脚标，因为要排序，之前的脚标乱了，通过这个函数找回来
    classCount={}          #['A':1]             #遍历脚标，求value值最大的那个，排完序，返回第一个
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createDataSet():
    group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels

##简单分类器测试
# group,labels = createDataSet()
# res = classify0([3,25],group,labels,3)
# print (res)

# 获取所有的样本矩阵和 样本的类型
def file2matrix(filename):
    fr = open(filename)
    numberOfLines = len(fr.readlines())         #得到有多少行
    returnMat = zeros((numberOfLines,3))        #返回一个 num行3列的数据，因为有三个属性
    classLabelVector = []                       #准备label值
    fr = open(filename)
    index = 0
    for line in fr.readlines():
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1]))
        index += 1
    return returnMat,classLabelVector

# 图形化展现
# import matplotlib
# import matplotlib.pyplot as plt
# datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
#
# fig = plt.figure()
# ax = fig.add_subplot(111)
# # 中间的数值是可以改变的，在处理多维的数据的时候，我们可以采取投影的方式可以更方便的解决问题
# ax.scatter(datingDataMat[:,0],datingDataMat[:,1],15.0*array(datingLabels),15.0*array(datingLabels))
# plt.show()

#归一化数据，因为dataset里面是的数据差别太大不便于计算，需要归一化
def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide
    return normDataSet, ranges, minVals  #返回归一化的列表，范围，以及最小值

#    用前50%数据来做测试，50%作为输入数据，统计分类结果错误率
def datingClassTest():
    hoRatio = 0.50      #hold out 10%
    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #加载数据
    normMat, ranges, minVals = autoNorm(datingDataMat) #归一化数据
    m = normMat.shape[0]   #得到行数
    numTestVecs = int(m*hoRatio) # 为了后500作先验数据，前500行用来做实验数据
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print ("the total error rate is: %f" % (errorCount/float(numTestVecs)))
    print (errorCount)

# 约会对象分类效果测试
#datingClassTest()

# 测试程序： 交互输入数据获取分类
def classifyPerson():
    resultList = ['根本不可能','有点希望','希望之星']
    percentTats = float(input("玩游戏所花时间百分比？"))
    ffMiles = float(input("每年的飞行里程？"))
    iceCream = float(input("每年吃几升冰激凌？"))
    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #load data setfrom file
    normMat, ranges, minVals = autoNorm(datingDataMat)
    inArr = array([ffMiles,percentTats,iceCream])
    classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels,3)
    print ("你对这个人的感觉：",resultList[classifierResult - 1])

classifyPerson()

----------------下面这段代码和上面的代码是相连的，只不过这段代码功能是识别图像文字

# 利用分类器进行手写数字识别测试
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

def handwritingClassTest():
    hwLabels = []
    trainingFileList = listdir('D:/PycharmProjects/machinelearningtest/knn/digits/trainingDigits')           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('D:/PycharmProjects/machinelearningtest/knn/digits/trainingDigits/%s' %fileNameStr)
    testFileList = listdir('D:/PycharmProjects/machinelearningtest/knn/digits/testDigits')        #iterate through the test set
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('D:/PycharmProjects/machinelearningtest/knn/digits/testDigits/%s' %fileNameStr)
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
        print "the classifier came back with: %d, the real answer is: %d" %(classifierResult, classNumStr)
        if (classifierResult != classNumStr): errorCount += 1.0
    print "\nthe total number of errors is: %d" %errorCount
    print "\nthe total error rate is: %f" %(errorCount/float(mTest))

# handwritingClassTest()

贝叶斯分类算法-----根据已知的知识去做判读分类

1.2 算法思想

朴素贝叶斯的思想是这样的：

如果一个事物在一些属性条件发生的情况下，事物属于A的概率>属于B的概率，则判定事物属于A

通俗来说比如，你在街上看到一个黑人，我让你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？

在你的脑海中，有这么一个判断流程：

1、这个人的肤色是黑色 <特征>

2、非洲人中黑色人种概率最高 <已知的是条件概率：p(黑色|非洲人)>

而用于判断的标准是：  P(非洲人|黑色)

3、没有其他辅助信息的情况下，最好的判断就是非洲人

这就是朴素贝叶斯的思想基础。

再扩展一下，假如某条街上，有100人，其中有50个美国人，50个非洲人，看到一个讲英语的黑人，那我们是怎么去判断他来自于哪里？

提取特征：

肤色： 黑

语言： 英语

先验知识：

P(黑色|非洲人) = 0.8

P(讲英语|非洲人)=0.1

P(黑色|美国人)= 0.2

P(讲英语|美国人)=0.9

要判断的概率是：

P(非洲人|(讲英语，黑色) )

P(美国人|(讲英语，黑色) )

思考过程：

P(非洲人|(讲英语，黑色) )   的 分子= 0.1 * 0.8 *0.5 =0.04

P(美国人|(讲英语，黑色) )   的 分子= 0.9 *0.2 * 0.5 = 0.09

从而比较这两个概率的大小就  等价于比较这两个分子的值：

可以得出结论，此人应该是 ：美国人

我们的判断结果就是：此人来自美国！

其蕴含的数学原理如下：

p(A|xy)=p(Axy)/p(xy)=p(Axy)/p(x)p(y)=p(A)/p(x)*p(A)/p(y)* p(xy)/p(xy)=p(A|x)p(A|y)

------------------------------------------------------------------------------------------------------

Kmean聚类算法

PS:这种方法是聚类
首先在待聚类的数据上选取基准点，可以为多个。然后根据其他点与所选基准点的距离进行分类。
那么，所得到的分类并不是很合适，然后继续对求新新的基准点，然后重复迭代，知道得到好的效果。

1.3.2 算法步骤图解

下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

--------------------------------------------------------------------------------------------

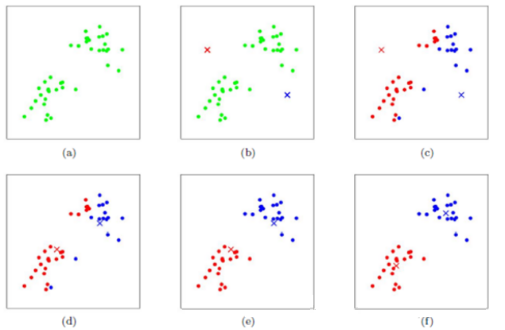
决策树分类算法

决策树分类算法的关键就是根据“先验数据”构造一棵最佳的决策树，用以预测未知数据的类别

决策树：是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

1.3.2 属性划分选择（即构造决策树）的依据

熵：信息论的奠基人香农定义的用来信息量的单位。简单来说，熵就是“无序，混乱”的程度。

通过计算来理解：

----------------------------------------------------------------------

支持向量机

就是为了解决发杂的点分类的，具体理解的不透彻