树和二叉树->最优二叉树

文字描述

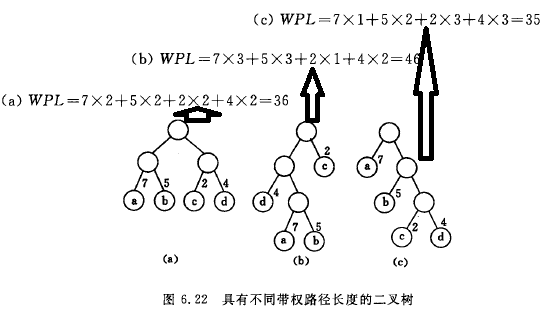
结点的路径长度

　　从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度。

树的路径长度

　　 从树根到每一个结点的路径长度之和叫树的路径长度。

结点的带权路径长度

　　从该结点到树根之间的路径长度与结点上权的乘积

树的带权路径长度

　　所有叶子结点的带权路径长度之和

最优二叉树或哈夫曼树

　　假设有n个权值{w1,w2, … ,wn},试构造一颗有n个叶子结点的二叉树，每个叶子结点带权wi，则其中带权路径长度WPL最小的二叉树称作最优二叉树或哈夫曼树。

哈夫曼算法

　　目的：构造一颗哈夫曼树

　　实现：

　　(1) 根据给定的n个权值{w1,w2, … ,wn}构成n棵二叉树的集合F={T1,T2,…,Tn}，其中每棵二叉树Ti中只有一个带权为wi的根结点，其左右子树均为空。

　　(2) 在F中选取两颗根结点的权值最小的树作为左右子树构造一颗新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。

　　(3) 在F中删除这两颗树，同时将新得到的二叉树加入F中

　　(4) 重复(2)和(3)，直到F只含一颗树为止。这颗树便是哈夫曼树。

哈夫曼编码

　　假设A、B、C、D的编码分别为00，01，10和11，则字符串’ABACCDA‘的电文便是’00010010101100’,对方接受时，可按二位一分进行译码。但有时希望电文总长尽可能的短， 如果让电文中出现次数较多的字符采用尽可能短的编码，则传送电文的总长鞭可减少。但是设计长短不等的编码，则必须是任一字符的编码都不是另一个字符的编码的前缀，以避免同样子电文串有多种译法，这种编码叫前缀编码。

　　又如何得到使电文总长最短的二进制前缀编码呢？假设字符串中有n种字符，每种字符在电文中出现的次数作为权，设计一颗哈夫曼树。左子树为0，右子树为1，走一条从根到叶子结点的路径进行编码。

哈夫曼译码

译码的过程是分解电文字符串，从根出发，按字符‘0‘或’1‘确定找左孩子或右孩子，直至叶子结点，便求得该子串相应的字符。

示意图

算法分析

略

代码实现

 /*
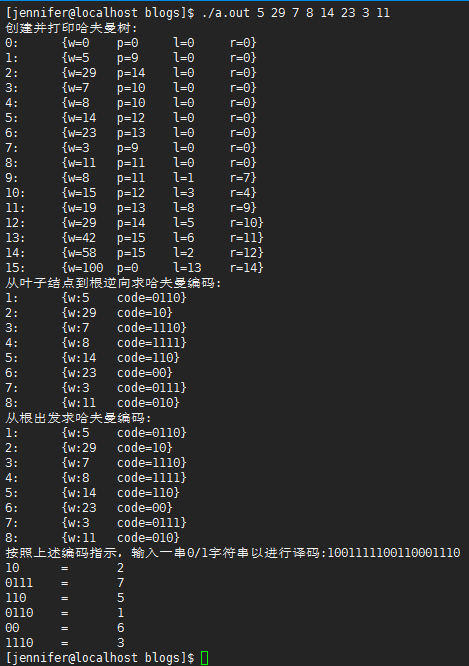
  ./a.out 5 29 7 8 14 23 3 11

  1001111100110001110
  */
 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define DEBUG
 //结点的最大个数
 #define MAX_SIZE 50

 //哈夫曼树和哈夫曼结点的存储结构
 typedef struct{
     unsigned int weight;
     unsigned int parent, lchild, rchild;
 }HNode, *HuffmanTree;

 //哈夫曼编码表的存储结构
 typedef char **HuffmanCode;

 /*
  * 在HT[1, ..., l]中选择parent为0且weight最小的两个结点，其序号分别为min1，min2
  */
 int Select(HuffmanTree HT, int l, int *min1, int *min2){
     int i = ;
     *min1 = *min2 = -;

     //找parent为0且weight最小的min1
     for(i=; i<=l; i++){
         if(!HT[i].parent){
             if(*min1<){
                 *min1 = i;
             }else if(HT[*min1].weight > HT[i].weight){
                 *min1 = i;
             }else{
                 //other
             }
         }else{
             //other
         }
     }

     //找parent为0且weight最小的min2
     for(i = ; i<=l; i++){
         if(!HT[i].parent && i!=*min1){
             if(*min2<){
                 *min2 = i;
             }else if(HT[*min2].weight > HT[i].weight){
                 *min2 = i;
             }else{
                 //other
             }
         }else{
             //other
         }
     }

     //确保min1<min2
     if(*min1 > *min2){
         i = *min1;
         *min1 = *min2;
         *min2 = i;
     }

     if((*min1<) && (*min2<)){
         return -;
     }else{
         return ;
     }
 }

 /*
  * 创建一颗哈夫曼树
  *
  * w存放n个字符的权值(权值都为非负数)，构造哈夫曼树HT， L表示哈夫曼树的长度(正常情况下为2*n-1)
  */
 void HuffmanCreate(int w[], int n, HuffmanTree *HT, int *L){
     if(n<=){
         return;
     }
     int m = *n-, i = , s1 = , s2 = ;
     //0号单元不用
     (*HT) = (HuffmanTree)malloc((m+)*sizeof(HNode));
     HuffmanTree p = *HT;
     *L = m;

     //给哈夫曼树的叶子结点赋值
     for(p=(*HT+), i = ; i<n; i++){
         p[i].weight = w[i];
         p[i].parent = p[i].lchild = p[i].rchild = ;
     }

     //给哈夫曼树的非叶子结点赋值
     for(i=n+; i<=m; ++i){
         //在HT[1,...,i-1]中选择parent为0且weight最小的两个结点，其序号分别为s1和s2
         if( Select(*HT, i-, &s1, &s2) < ){
             break;
         }
         //用s1和s2作为左右子树构造一颗新的二叉树
         (*HT)[s1].parent = (*HT)[s2].parent = i;
         (*HT)[i].lchild = s1;
         (*HT)[i].rchild = s2;
         //置新的二叉树的根结点的权值为其左右子树上根结点的权值之和
         (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
     }
     return;
 }

 /*
  * 哈夫曼编码
  *
  * 从叶子到根逆向求每个字符的哈夫曼编码
  */
 void HuffmanEncoding_1(HuffmanTree HT, HuffmanCode *HC, int n){
     //分配n个字符编码的头指针向量
     *HC = (HuffmanCode)malloc((n+)*sizeof(char *));
     //分配求编码的工作空间
     char *cd = (char*)malloc(n+sizeof(char));
     //编码结束符
     cd[n-] = '\0';
     int i = , start = , c = , f = ;
     //逐个字符求哈夫曼编码
     for(i=; i<=n; i++){
         //编码结束位置
         start = n-;
         //从叶子到根逆向求编码
         for(c=i, f=HT[i].parent; f!=; c = f, f=HT[f].parent){
             if(HT[f].lchild == c){
                 cd[--start] = '';
             }else{
                 cd[--start] = '';
             }
         }
         //为第i个字符编码分配空间
         (*HC)[i-] = (char*)malloc((n-start)*sizeof(char));
         //从cd复制编码到HC
         strncpy((*HC)[i-], cd+start, n-start);
     }
     //释放工作空间
     free(cd);
     return ;
 }

 /*
  * 哈夫曼编码
  *
  * 从根出发，遍历整个哈夫曼树，求得各个叶子结点所表示的字符的哈夫曼编码
  */
 void HuffmanEncoding_2(HuffmanTree HT, HuffmanCode *HC, int n){
     *HC = (HuffmanCode)malloc((n+)*sizeof(char *));
     int p = *n-;
     int cdlen = ;
     int i = ;
     char *cd = (char*)malloc(n+sizeof(char));
     //利用weight，当作遍历哈夫曼树时的结点状态标志
     for(i=; i<=(*n-); i++){
         HT[i].weight = ;
     }
     while(p){
         if(HT[p].weight == ){
             //向左
             HT[p].weight = ;
             if(HT[p].lchild != ){
                 p = HT[p].lchild;
                 cd[cdlen++] = '';
             }else if(HT[p].rchild == ){
                 //登记叶子结点的字符的编码
                 (*HC)[p-] = (char *)malloc((cdlen+)*sizeof(char));
                 memset((*HC)[p-], , (cdlen+)*sizeof(char));
                 cd[cdlen] = '\0';
                 //复制编码
                 strncpy((*HC)[p-], cd, cdlen);
             }
         }else if(HT[p].weight == ){
             //向右
             HT[p].weight = ;
             if(HT[p].rchild != ){
                 p = HT[p].rchild;
                 cd[cdlen++] = '';
             }
         }else{
             //退到父结点，编码长度减1
             HT[p].weight = ;
             p = HT[p].parent;
             --cdlen;
         }
     }
 }

 /*
  *哈夫曼译码
  *
  *从根出发走向叶子结点，找到叶子结点后输出该结点的下标值，然后返回根结点重复，直至读完。
  */
 void HuffmanDecoding(HuffmanTree HT, int n, char str[], size_t len)
 {
     //
     int p = *n-;
     int i = ;
     while(i < len){
         printf("%c",str[i]);
         if(str[i] == ''){
             //走向左孩子
             p = HT[p].lchild;
         }else if(str[i] == ''){
             //走向右孩子
             p = HT[p].rchild;
         }else{
             printf("unexcepted char %c!!!\n", str[i]);
             return;
         }
         //看是否走到叶子结点
         if(p<=n){
             //输出结点的下标值，并返回根结点
             printf("\t=\t%d\n", p);
             p = *n-;
         }
         i+=;
     }
     return ;
 }

 void HuffmanPrint(HuffmanTree HT, int L){
     if(L<=)
         return ;
     int i = ;
     for(i=; i<=L; i++){
         printf("%d:\t{w=%d\tp=%d\tl=%d\tr=%d}\n", i, HT[i].weight, HT[i].parent, HT[i].lchild, HT[i].rchild);
     }
 }

 int main(int argc, char *argv[])
 {
     if(argc < ){
         return -;
     }

     int i = , L = ;
     int w[MAX_SIZE] = {};
     HuffmanTree HT = NULL;

     for(i=; i<argc; i++){
         w[i-] = atoi(argv[i]);
     }
 #ifdef DEBUG
     printf("创建并打印哈夫曼树:\n");
 #endif
     HuffmanCreate(w, i-, &HT, &L);
     HuffmanPrint(HT, L);

 #ifdef DEBUG
     printf("从叶子结点到根逆向求哈夫曼编码:\n");
 #endif
     HuffmanCode HC;
     HuffmanEncoding_1(HT, &HC, i-);

 #ifdef DEBUG
     int j = ;
     for(j=; j<i-; j++){
         printf("%d:\t{w:%d\tcode=%s}\n", j+, w[j], HC[j]);
         free(HC[j]);
     }
     free(HC);
 #endif

 #ifdef DEBUG
     printf("从根出发求哈夫曼编码:\n");
 #endif
     HuffmanEncoding_2(HT, &HC, i-);

 #ifdef DEBUG
     for(j=; j<i-; j++){
         printf("%d:\t{w:%d\tcode=%s}\n", j+, w[j], HC[j]);
         free(HC[j]);
     }
     free(HC);
 #endif

     printf("按照上述编码指示，输入一串0/1字符串以进行译码:");
     char str[] = {};
     scanf("%s", &str);
     HuffmanDecoding(HT, i-, str, strlen(str));
     return ;
 }

最优二叉树

 运行