hdu 6134 Battlestation Operational 莫比乌斯反演

Battlestation Operational

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Problem Description

> The Death Star, known officially as the DS-1 Orbital Battle Station, also known as the Death Star I, the First Death Star, Project Stardust internally, and simply the Ultimate Weapon in early development stages, was a moon-sized, deep-space mobile battle station constructed by the Galactic Empire. Designed to fire a single planet-destroying superlaser powered by massive kyber crystals, it was the pet project of the Emperor, Darth Vader, and its eventual commander Grand Moff Wilhuff Tarkin to expound the military philosophy of the aptly named Tarkin Doctrine.
>
> — Wookieepedia

In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.

You are assigned the task to estimate the damage of one shot of the Superlaser.

Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i<j.

The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.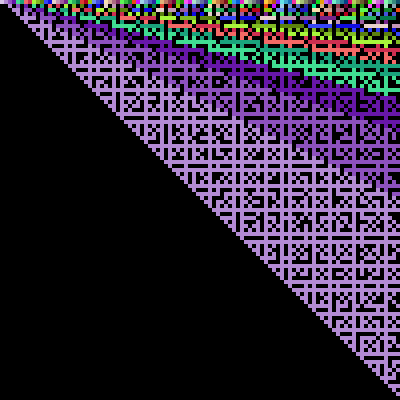

Your should calculate the total damage to the battlefield. Formally, you should compute

f(n)=∑i=1n∑j=1i⌈ij⌉[(i,j)=1],

where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.

 

Input

There are multiple test cases.

Each line of the input, there is an integer n (1≤n≤106), as described in the problem.

There are up to 104 test cases.

 

Output

For each test case, output one integer in one line denoting the total damage of the Superlaser, f(n) mod 109+7.

 

Sample Input

1
2
3
10

 

Sample Output

1
3
8
110

 

Source

2017 Multi-University Training Contest - Team 8

　不想写题解！！！！！！！！！

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
#include<bitset>
#include<time.h>
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define pi (4*atan(1.0))
#define eps 1e-4
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=3e4+,M=1e6+,inf=1e9+,MOD=1e9+;
const LL INF=1e18+,mod=1e9+;

int mu[M], p[M], np[M], cnt;
LL smu[M];
void init()
{
    mu[]=;
    for(int i=; i<M; ++i)
    {
        if(!np[i]) p[++cnt]=i, mu[i]=-;
        for(int j=; j<=cnt && i*p[j]<M ; ++j)
        {
            int t=i*p[j];
            np[t]=;
            if(i%p[j]==)
            {
                mu[t]=;
                break;
            }
            mu[t]=-mu[i];
        }
    }
    for(int i=; i<M; i++)
        smu[i]=smu[i-]+mu[i],smu[i]=(smu[i]%mod+mod)%mod;
}
LL a[M],sum[M],sum2[M];
void init1()
{
    for(int j=; j<=; j++)
    {
        a[j]+=;
        a[j+]-=;
        a[j+]=(a[j+]%mod+mod)%mod;
        a[j]=(a[j]%mod+mod)%mod;
        for(int k=;;k++)
        {
            int L=(k-)*j+;
            int R=k*j+;
            a[L]+=k;
            a[L]%=mod;
            if(R>=M)break;
            a[R]-=k;
            a[R]=(a[R]%mod+mod)%mod;
        }
    }
    for(int i=; i<M; i++)
        sum[i]=sum[i-]+a[i],sum[i]%=mod;
    for(int i=;i<M;i++)
        sum2[i]=sum2[i-]+sum[i],sum2[i]%=mod;
}
int main()
{
    init();
    init1();
    int n;
    while(~scanf("%d",&n))
    {
        LL ans=;
        int last=;
        for(int i=; i<=n; i=last+)
        {
            last=(n/(n/i));
            ans+=(((smu[last]-smu[i-]+mod)%mod)*sum2[n/i])%mod;
            ans=(ans%mod+mod)%mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}

Battlestation Operational

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 20    Accepted Submission(s): 3

Problem Description

> The Death Star, known officially as the DS-1 Orbital Battle Station, also known as the Death Star I, the First Death Star, Project Stardust internally, and simply the Ultimate Weapon in early development stages, was a moon-sized, deep-space mobile battle station constructed by the Galactic Empire. Designed to fire a single planet-destroying superlaser powered by massive kyber crystals, it was the pet project of the Emperor, Darth Vader, and its eventual commander Grand Moff Wilhuff Tarkin to expound the military philosophy of the aptly named Tarkin Doctrine.
>
> — Wookieepedia

In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.

You are assigned the task to estimate the damage of one shot of the Superlaser.

Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i<j.

The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.

Your should calculate the total damage to the battlefield. Formally, you should compute

f(n)=∑i=1n∑j=1i⌈ij⌉[(i,j)=1],

where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.

 

Input

There are multiple test cases.

Each line of the input, there is an integer n (1≤n≤106), as described in the problem.

There are up to 104 test cases.

 

Output

For each test case, output one integer in one line denoting the total damage of the Superlaser, f(n) mod 109+7.

 

Sample Input

1
2
3
10

 

Sample Output

1
3
8
110

 

Source

2017 Multi-University Training Contest - Team 8