(转) Let’s make an A3C: Theory

本文转自：https://jaromiru.com/2017/02/16/lets-make-an-a3c-theory/

Let’s make an A3C: Theory

February 16, 2017A3C

This article is part of series Let’s make an A3C.

1. Theory
2. Implementation (TBD)

Introduction

Policy Gradient Methods is an interesting family of Reinforcement Learning algorithms. They have a long history1, but only recently were backed by neural networks and had success in high-dimensional cases. A3C algorithm was published in 2016 and can do better than DQN with a fraction of time and resources2.

In this series of articles we will explain the theory behind Policy Gradient Methods, A3C algorithm and develop a simple agent in Python.

It is very recommended to have read at least the first Theory article from Let’s make a DQNseries which explains theory behind Reinforcement Learning (RL). We will also make comparison to DQN and make references to these older series.

Background

Let’s review the RL basics. An agent exists in an environment, which evolves in discrete time steps. Agent can influence the environment by taking an action a each time step, after which it receives a reward r and an observed state s. For simplification, we only consider deterministic environments. That means that taking action a in state s always results in the same state s’.

Although these high level concepts stay the same as in DQN case, they are some important changes in Policy Gradient (PG) Methods. To understand the following, we have to make some definitions.

First, agent’s actions are determined by a stochastic policy π(s). Stochastic policy means that it does not output a single action, but a distribution of probabilities over actions, which sum to 1.0. We’ll also use a notation π(a|s) which means the probability of taking action a in state s.

For clarity, note that there is no concept of greedy policy in this case. The policy π does not maximize any value. It is simply a function of a state s, returning probabilities for all possible actions.

We will also use a concept of expectation of some value. Expectation of value X in a probability distribution P is:


where  are all possible values of X and  their probabilities of occurrence. It can also be viewed as a weighted average of values  with weights .

The important thing here is that if we had a pool of values X, ratio of which was given by P, and we randomly picked a number of these, we would expect the mean of them to be . And the mean would get closer to  as the number of samples rise.

We’ll use the concept of expectation right away. We define a value function V(s) of policy π as an expected discounted return, which can be viewed as a following recurrent definition:

Basically, we weight-average the  for every possible action we can take in state s. Note again that there is no max, we are simply averaging.

Action-value function Q(s, a) is on the other hand defined plainly as:

simply because the action is given and there is only one following s’.

Now, let’s define a new function A(s, a) as:


We call A(s, a) an advantage function and it expresses how good it is to take an action a in a state s compared to average. If the action a is better than average, the advantage function is positive, if worse, it is negative.

And last, let’s define  as some distribution of states, saying what the probability of being in some state is. We’ll use two notations – , which gives us a distribution of starting states in the environment and , which gives us a distribution of states under policy π. In other words, it gives us probabilities of being in a state when following policy π.

Policy Gradient

When we built the DQN agent, we used a neural network to approximate the Q(s, a) function. But now we will take a different approach. The policy π is just a function of state s, so we can approximate directly that. Our neural network with weights  will now take an state s as an input and output an action probability distribution, . From now on, by writing π it is meant , a policy parametrized by the network weights .

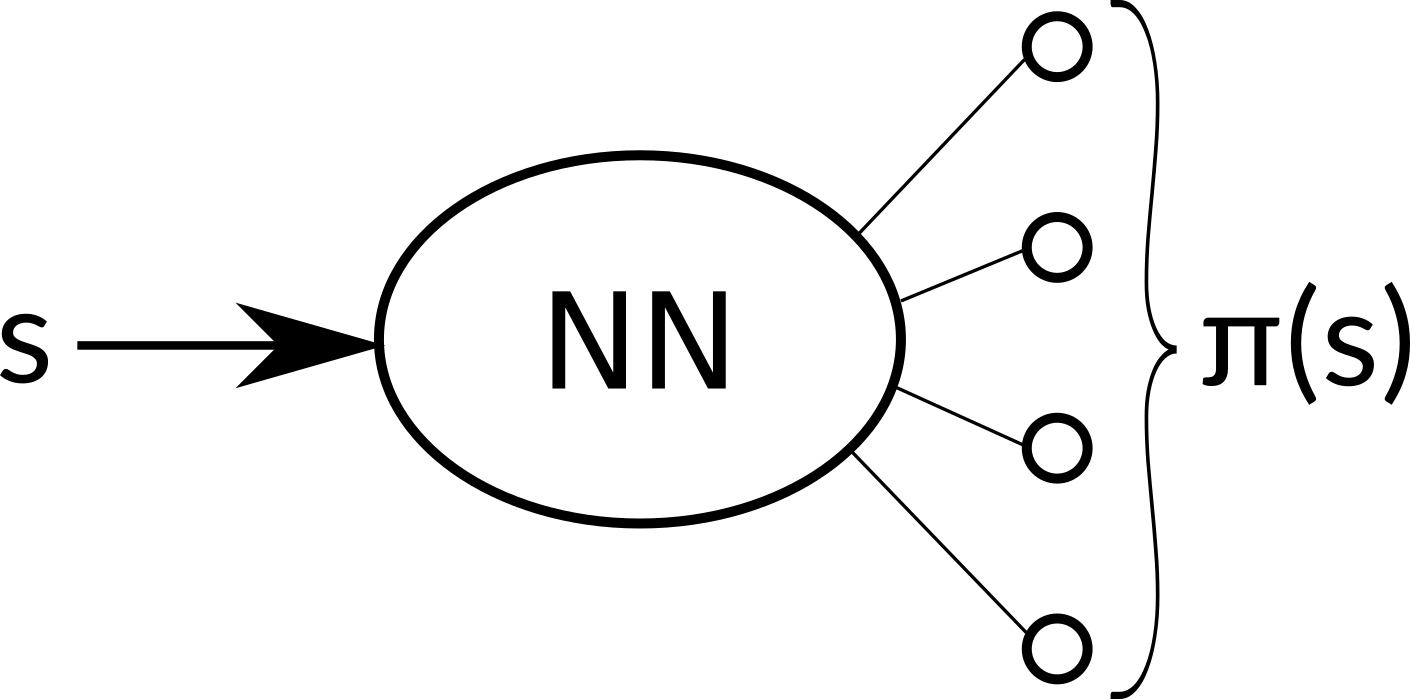
In practice, we can take an action according to this distribution or simply take the action with the highest probability, both approaches have their pros and cons.

But we want the policy to get better, so how do we optimize it? First, we need some metric that will tell us how good a policy is. Let’s define a function  as a discounted reward that a policy π can gain, averaged over all possible starting states .

We can agree that this metric truly expresses, how good a policy is. The problem is that it’s hard to estimate. Good news are, that we don’t have to.

What we truly care about is how to improve this quantity. If we knew the gradient of this function, it would be trivial. Surprisingly, it turns out that there’s easily computable gradient of  function in the following form:

I understand that the step from  to  looks a bit mysterious, but a proof is out of scope of this article. The formula above is derived in the Policy Gradient Theorem3 and you can look it up if you want to delve into quite a piece of mathematics. I also direct you to a more digestible online lecture4, where David Silver explains the theorem and also a concept of baseline, which I already incorporated.

The formula might seem intimidating, but it’s actually quite intuitive when it’s broken down. First, what does it say? It informs us in what direction we have to change the weights of the neural network if we want the function  to improve.

Let’s look at the right side of the expression. The second term inside the expectation, , tells us a direction in which logged probability of taking action a in state s rises. Simply said, how to make this action in this context more probable.

The first term, , is a scalar value and tells us what’s the advantage of taking this action. Combined we see that likelihood of actions that are better than average is increased, and likelihood of actions worse than average is decreased. That sounds like a right thing to do.

Both terms are inside an expectation over state and action distribution of π. However, we can’t exactly compute it over every state and every action. Instead, we can use that nice property of expectation that the mean of samples with these distributions lays near the expected value.

Fortunately, running an episode with a policy π yields samples distributed exactly as we need. States encountered and actions taken are indeed an unbiased sample from the  and π(s)distributions.

That’s great news. We can simply let our agent run in the environment and record the (s, a, r, s’) samples. When we gather enough of them, we use the formula above to find a good approximation of the gradient . We can then use any of the existing techniques based on gradient descend to improve our policy.

Actor-critic

One thing that remains to be explained is how we compute the A(s, a) term. Let’s expand the definition:

A sample from a run can give us an unbiased estimate of the Q(s, a) function. We can also see that it is sufficient to know the value function V(s) to compute A(s, a).

The value function can also be approximated by a neural network, just as we did with action-value function in DQN. Compared to that, it’s easier to learn, because there is only one value for each state.

What’s more, we can use the same neural network for estimating π(s) to estimate V(s). This has multiple benefits. Because we optimize both of these goals together, we learn much faster and effectively. Separate networks would very probably learn very similar low level features, which is obviously superfluous. Optimizing both goals together also acts as a regularizing element and leads to a greater stability. Exact details on how to train our network will be explained in the next article. The final architecture then looks like this:

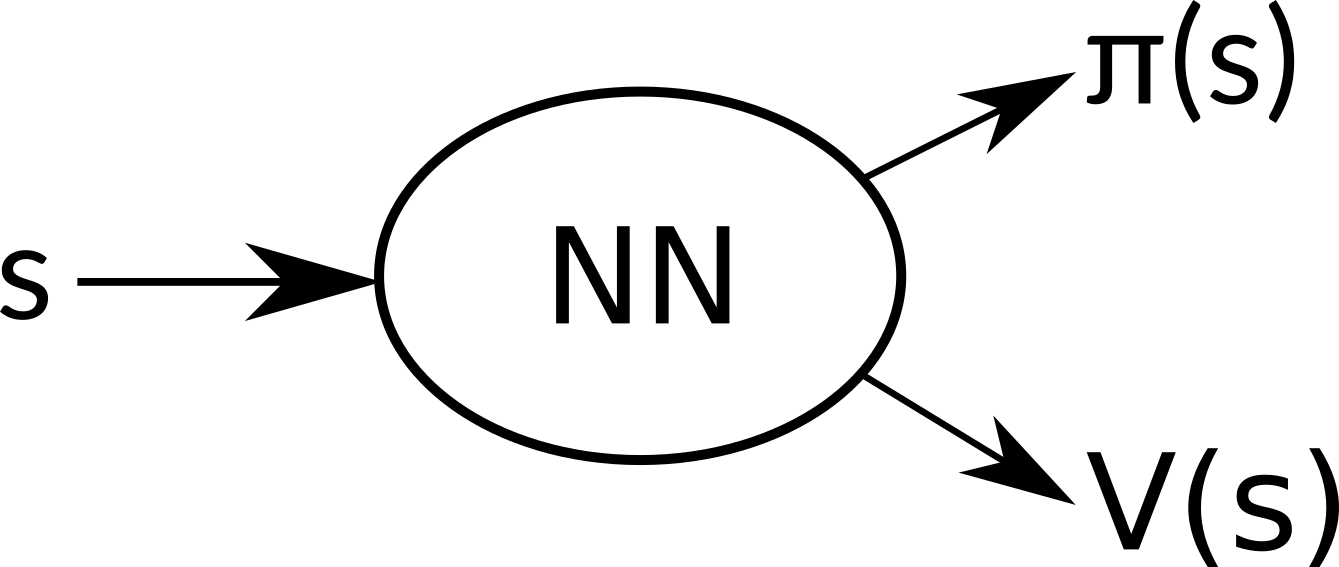
Our neural network share all hidden layers and outputs two sets – π(s) and V(s).

So we have two different concepts working together. The goal of the first one is to optimize the policy, so it performs better. This part is called actor. The second is trying to estimate the value function, to make it more precise. That is called critic. I believe these terms arose from the Policy Gradient Theorem:

The actor acts, and the critic gives insight into what is a good action and what is bad.

Parallel agents

The samples we gather during a run of an agent are highly correlated. If we use them as they arrive, we quickly run into issues of online learning. In DQN, we used a technique named Experience Replay to overcome this issue. We stored the samples in a memory and retrieved them in random order to form a batch.

But there’s another way to break this correlation while still using online learning. We can run several agents in parallel, each with its own copy of the environment, and use their samples as they arrive. Different agents will likely experience different states and transitions, thus avoiding the correlation2. Another benefit is that this approach needs much less memory, because we don’t need to store the samples.

This is the approach the A3C algorithm takes. The full name is Asynchronous advantage actor-critic (A3C) and now you should be able to understand why.

Conclusion

We learned the fundamental theory behind PG methods and will use this knowledge to implement an agent in the next article. We will explain how to use the gradients to train the neural network with our familiar tools, Python, Keras and newly TensorFlow.

References

---

1. Williams, R., Simple statistical gradient-following algorithms for connectionist reinforcement learning, Machine Learning, 1992
2. Mnih, V. et al., Asynchronous methods for deep reinforcement learning, ICML, 2016
3. Sutton, R. et al., Policy Gradient Methods for Reinforcement Learning with Function Approximation, NIPS, 1999
4. Silver, D., Policy Gradient Methods, https://www.youtube.com/watch?v=KHZVXao4qXs, 2015

Share this article:

• Share on Facebook (Opens in new window)
• Click to share on Google+ (Opens in new window)
• Click to share on Twitter (Opens in new window)

Post navigation

← Let’s make a DQN: Double Learning and Prioritized Experience Replay

Leave a Reply

 

 

• Follow