Opencv笔记（二十一）——傅里叶变换

参考

Numpy 中的傅里叶变换

首先我们看看如何使用 Numpy 进行傅里叶变换。Numpy 中的 FFT 包可以帮助我们实现快速傅里叶变换。函数 np.fft.fft2() 可以对信号进行频率转换,输出结果是一个复杂的数组。本函数的第一个参数是输入图像,要求是灰度格式。第二个参数是可选的, 决定输出数组的大小。输出数组的大小和输入图像大小一样。如果输出结果比输入图像大,输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话,输入图像就会被切割。

频率为0 的部分(直流分量)在输出图像的左上角。(2D傅里叶变换F(x,y)的F(0,0)位置在图像的左上角,F(0,0)表示的是图像灰度的均值)如果想让它(直流分量)在输出图像的中心,我们还需要将结果沿两个方向平移 N/2 。函数 np.fft.fftshift() 可以帮助我们实现这一步。

# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread("/home/wl/3.jpg", 0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 这里构建振幅图的公式没学过
magnitude_spectrum = 20*np.log(np.abs(fshift))#先取绝对值,表示取模。取对数,将数据范围变小
print magnitude_spectrum
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum , cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

我们可以看到输出结果的中心部分更白(亮),这说明低频分量更多。现在我们可以进行频域变换了,我们就可以在频域对图像进行一些操作了,例如高通滤波和重建图像(DFT 的逆变换)。比如我们可以使用一个60x60 的矩形窗口对图像进行掩模操作从而去除低频分量。然后再使用函数np.fft.ifftshift() 进行逆平移操作,所以现在直流分量又回到左上角了,左后使用函数 np.ifft2() 进行 FFT 逆变换。同样又得到一堆复杂的数字,我们可以对他们取绝对值:

# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread("/home/wl/3.jpg", 0)
f = np.fft.fft2(img)#得到结果为复数矩阵
fshift = np.fft.fftshift(f)#直接取中心
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0#蒙板大小60×60
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)#使用FFT逆变换,此时结果仍然是复数
img_back = np.abs(img_back)# 取绝对值
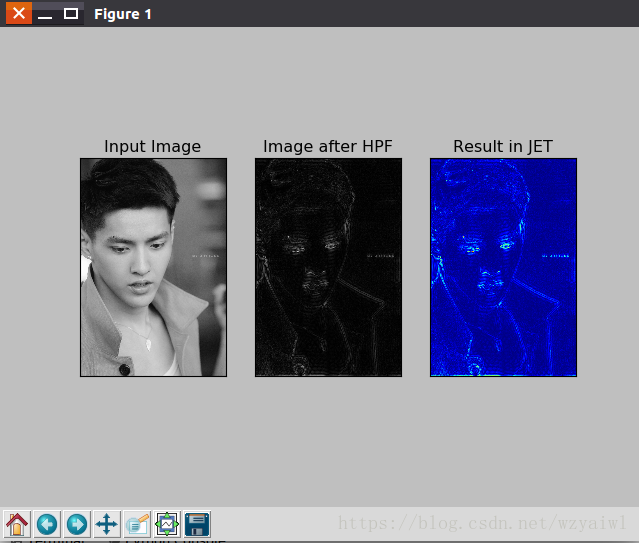
plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(img_back, cmap = 'gray')
plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(img_back)
plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()

上图的结果显示高通滤波其实是一种边界检测操作。这就是我们在前面图像梯度那一章看到的。同时我们还发现图像中的大部分数据集中在频谱图的低频区域。

OpenCV 中的傅里叶变换

OpenCV 中相应的函数是 cv2.dft() 和 cv2.idft()。和前面输出的结果一样,但是是双通道的。第一个通道是结果的实数部分,第二个通道是结果的虚数部分。输入图像要首先转换成 np.float32 格式。

# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread("/home/wl/3.jpg", 0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))#频谱图
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

使用函数 cv2.cartToPolar()会同时得到幅度和相位,此函数也是直角坐标转换为极坐标的函数。

现在我们来做逆 DFT。在前面的部分我们实现了一个 HPF(高通滤波),现在我们来做 LPF(低通滤波)将高频部分去除。其实就是对图像进行模糊操作。首先我们需要构建一个掩模,与低频区域对应的地方设置为 1, 与高频区域对应的地方设置为 0。

# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread("/home/wl/3.jpg", 0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
rows, cols = img.shape
crow,ccol = rows/2 , cols/2
# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

注意:OpenCV 中的函数 cv2.dft() 和 cv2.idft() 要比 Numpy 快。但是Numpy 函数更加用户友好。

DFT 的性能优化

当数组的大小为某些值时 DFT 的性能会更好。当数组的大小是 2 的指数时 DFT 效率最高。当数组的大小是 2,3,5 的倍数时效率也会很高。所以如果你想提高代码的运行效率时,你可以修改输入图像的大小(补 0)。对于OpenCV 你必须自己手动补 0。但是 Numpy,你只需要指定 FFT 运算的大小,它会自动补 0。那我们怎样确定最佳大小呢?OpenCV 提供了一个函数:cv2.getOptimalDFTSize()。它可以同时被 cv2.dft() 和 np.fft.fft2() 使用。

# coding=utf-8
import cv2
import numpy as np

img = cv2.imread("/home/wl/3.jpg", 0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
rows, cols = img.shape
print rows,cols
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print nrows,ncols

1420 946
1440 960