NOIP模拟题 2017.7.3 - 模拟 - 贪心 - 记忆化搜索
直接暴力模拟，注意判数据结构为空时的取出操作。
Code
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << ) - );
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
char x;
int aFlag = ;
while(!isdigit((x = getchar())) && x != '-' && x != -);
if(x == -) {
ungetc(x, stdin);
return false;
}
if(x == '-'){
x = getchar();
aFlag = -;
}
for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
ungetc(x, stdin);
u *= aFlag;
return true;
} int n;
stack<int> s;
queue<int> q;
priority_queue<int> que;
boolean prob[] = {true, true, true}; inline void solve() {
int opt, a, x;
readInteger(n);
while(n--) {
readInteger(opt);
readInteger(a);
if(opt == ) {
if(prob[]) s.push(a);
if(prob[]) q.push(a);
if(prob[]) que.push(a);
} else {
if(prob[]) {
if(s.empty()) prob[] = false;
else {
x = s.top();s.pop();
if(x != a) prob[] = false;
}
}
if(prob[]) {
if(q.empty()) prob[] = false;
else {
x = q.front();q.pop();
if(x != a) prob[] = false;
}
}
if(prob[]) {
if(que.empty()) prob[] = false;
else {
x = que.top();que.pop();
if(x != a) prob[] = false;
}
}
}
}
puts(prob[] ? "YES" : "No");
puts(prob[] ? "YES" : "No");
puts(prob[] ? "YES" : "No");
} int main() {
freopen("qu.in", "r", stdin);
freopen("qu.out", "w", stdout);
solve();
return ;
}
考虑只有两个任务的时候，只有两种情况，它们的答案分别是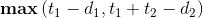
和
。又因为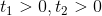
,所以有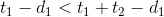
，
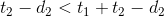，所以它们的谁更优取决于
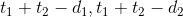。即d值的大小。
现在考虑多个任务的时候，先随便安排一种执行任务的顺序，如果存在有关d值的逆序对，那么说明当前这个顺序一定不优，我们可以通过交换相邻的一对逆序对使得结果更优。最优时即不存在有关d的逆序对吗，即按d值排序再计算答案就好了。
Code
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << ) - );
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
char x;
int aFlag = ;
while(!isdigit((x = getchar())) && x != '-' && x != -);
if(x == -) {
ungetc(x, stdin);
return false;
}
if(x == '-'){
x = getchar();
aFlag = -;
}
for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
ungetc(x, stdin);
u *= aFlag;
return true;
} typedef class Task {
public:
int t;
int d; Task(int t = , int d = ):t(t), d(d) { } boolean operator < (Task b) const {
if(d != b.d) return d < b.d;
return t < b.t;
}
}Task; int n;
Task* ts; inline void init() {
readInteger(n);
ts = new Task[(const int)(n + )];
for(int i = ; i <= n; i++) {
readInteger(ts[i].t);
readInteger(ts[i].d);
}
} int res = ;
inline void solve() {
sort(ts + , ts + n + );
int fin = ;
for(int i = ; i <= n; i++) {
fin += ts[i].t;
smax(res, max(, fin - ts[i].d));
}
printf("%d\n", res);
} int main() {
freopen("ming.in", "r", stdin);
freopen("ming.out", "w", stdout);
init();
solve();
return ;
}
先说一下70分做法(由于数据比较水，所以暴力基本上可以过7个点)吧。
- 暴力建图，然后用树归去统计。每到一个点，先统计它所在的子树的大小。然后用当前子树大小乘它和这个新树的大小再乘它到父节点的那条边的权(乘法原理)。累加起来就是答案。
- 这种做法不用建图，首先可以直接求的几个量:连接两棵树的边对答案的贡献，两边的树内部的路径对答案的贡献。现在我们希望求得经过这条边的路径对答案的贡献。根据人生的哲理和组合计数上的经验，我们可以轻松得到这个长度等于左边所有到左边连接点的路径距离总和乘右边节点数，对于右边同理。现在想要快速在O(n)的时间内处理掉这个路径长度总和又不建树，就可以按边一直分下去(类似于边分治吧)。
我先画一幅图: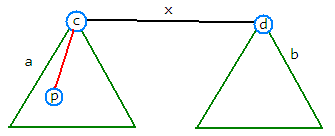
显然在子树b内，可以求出其中的点到点d的距离和，在子树a内也可以用一样的方法求出其中的点到点p的距离，随后是不是还差了点什么?好像子树b内的路径没有延伸到点p。因为树上的路径是唯一的，我们只需要补上路径d-c-p的长度乘子树b内节点数就可以求答案。
我在考试的时候用的是方法1。
Code
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << ) - );
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
char x;
int aFlag = ;
while(!isdigit((x = getchar())) && x != '-' && x != -);
if(x == -) {
ungetc(x, stdin);
return false;
}
if(x == '-'){
x = getchar();
aFlag = -;
}
for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
ungetc(x, stdin);
u *= aFlag;
return true;
} ///map template starts
typedef class Edge{
public:
int end;
int next;
int w;
Edge(const int end = , const int next = , const int w = ):end(end), next(next), w(w){}
}Edge; typedef class MapManager{
public:
int ce;
int *h;
Edge *edge;
MapManager(){}
MapManager(int points, int limit):ce(){
h = new int[(const int)(points + )];
edge = new Edge[(const int)(limit + )];
memset(h, , sizeof(int) * (points + ));
}
inline void addEdge(int from, int end, int w){
edge[++ce] = Edge(end, h[from], w);
h[from] = ce;
}
inline void addDoubleEdge(int from, int end, int w){
addEdge(from, end, w);
addEdge(end, from, w);
}
Edge& operator [] (int pos) {
return edge[pos];
}
}MapManager;
#define m_begin(g, i) (g).h[(i)]
///map template ends const int moder = 1e9 + ; int n;
MapManager *g;
int* siz;
int s[]; // The size of node i.
int fs[]; // The length of a edge which connects node i and its father node. inline int mod_plus(int a, int b) {
int ret = a + b;
while(ret >= moder) ret -= moder;
return ret;
} inline void init() {
readInteger(n);
g = new MapManager[(const int)(n + )];
siz = new int[(const int)(n + )];
siz[] = ;
g[] = MapManager(, );
} int cnt = ;
inline void mknewtree(int a, int b, int c, int d, int l) { // Make a new tree following the recipe within O(n).
cnt++;
siz[cnt] = siz[a] + siz[b];
g[cnt] = MapManager(siz[cnt], siz[cnt] << );
for(int i = ; i < siz[a]; i++)
for(int j = m_begin(g[a], i); j; j = g[a][j].next)
g[cnt].addEdge(i, g[a][j].end, g[a][j].w);
for(int i = ; i < siz[b]; i++)
for(int j = m_begin(g[b], i); j; j = g[b][j].next)
g[cnt].addEdge(i + siz[a], g[b][j].end + siz[a], g[b][j].w);
g[cnt].addDoubleEdge(c, d + siz[a], l);
} int res = ;
void calcLength(int node, int fa) {
s[node] = ;
for(int i = m_begin(g[cnt], node); i; i = g[cnt][i].next) {
int& e = g[cnt][i].end;
if(e == fa) continue;
fs[e] = g[cnt][i].w;
calcLength(e, node);
s[node] += s[e];
}
res = mod_plus(res ,(s[node] * 1LL * (siz[cnt] - s[node]) * fs[node]) % moder);
} inline void solve() {
int a, b, c, d, l;
while(n--) {
readInteger(a);
readInteger(b);
readInteger(c);
readInteger(d);
readInteger(l);
mknewtree(a, b, c, d, l);
res = , fs[] = ;
calcLength(, -);
printf("%d\n", res);
}
} int main() {
freopen("zi.in", "r", stdin);
freopen("zi.out", "w", stdout);
init();
solve();
return ;
}
70分做法
方法1似乎无法优化了，但是方法2很有搞头，因为不用建树。你可以试试人工模拟几组数据，然后你会惊讶地发现真正的状态数并不多，大概也就O(m2)吧，对于树上任意两点的距离，也就顶多连接点的组合，而这些点的（不同树上的总共）个数都是O(m)的。而考虑树上一棵树到其任意一点的距离总和，也就是到的都是连接点，数量也不多。因此2个map强势登场一堆记忆化加上直接把这道题水掉了。。
如果还不清楚就结合代码看吧。
Code
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#include<stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << ) - );
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
char x;
int aFlag = ;
while(!isdigit((x = getchar())) && x != '-' && x != -);
if(x == -) {
ungetc(x, stdin);
return false;
}
if(x == '-'){
x = getchar();
aFlag = -;
}
for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
ungetc(x, stdin);
u *= aFlag;
return true;
} #define LL long long template<typename T1, typename T2>
inline pair<T1, T2> mkpair(T1 a, T2 b) {
return pair<T1, T2>(a, b);
} const LL moder = 1e9 + ; LL n;
LL *a, *b, *l;
LL *c, *d;
LL* siz;
LL* res; inline LL mod_plus(LL a, LL b) {
LL ret = a + b;
// while(ret >= moder) ret -= moder;
return ret % moder;
} inline void init() {
readInteger(n);
siz = new LL[(const LL)(n + )];
siz[] = ;
a = new LL[(const LL)(n + )];
b = new LL[(const LL)(n + )];
c = new LL[(const LL)(n + )];
d = new LL[(const LL)(n + )];
l = new LL[(const LL)(n + )];
res = new LL[(const LL)(n + )];
for(LL i = ; i <= n; i++) {
readInteger(a[i]);
readInteger(b[i]);
readInteger(c[i]);
readInteger(d[i]);
readInteger(l[i]);
siz[i] = siz[a[i]] + siz[b[i]];
}
} map<pair<LL, pair<LL, LL> >, LL> dis; // Records the distance between node u and node v in tree tr.
map<pair<LL, LL>, LL> D; // Records LL length(LL tr, LL u, LL v) { // Calculate the distance from node u to node v
if(tr == ) return ;
pair<LL, pair<LL, LL> > key = mkpair(tr, mkpair(u, v));
if(dis.count(key)) return dis[key];
LL ls = siz[a[tr]];
LL ret;
if(u < ls && v < ls) ret = length(a[tr], u, v);
else if(u >= ls && v >= ls) ret = length(b[tr], u - ls, v - ls);
else {
if(u > v) swap(u, v);
ret = mod_plus(mod_plus(length(a[tr], u, c[tr]), l[tr]), length(b[tr], v - ls, d[tr]));
}
return dis[key] = ret;
} LL calc(LL tr, LL p) { // Calculate the distance from all the nodes in tree tr to node p in tree tr
if(tr == ) return ;
pair<LL, LL> key = mkpair(tr, p);
if(D.count(key)) return D[key];
LL ls = siz[a[tr]];
LL ret;
if(p < ls) { // Node p is in tree a[tr].
ret = (length(tr, d[tr] + ls, p) * 1LL * siz[b[tr]]) % moder;
ret = mod_plus(ret, calc(a[tr], p));
ret = mod_plus(ret, calc(b[tr], d[tr]));
} else { // Otherwise node p is in tree b[tr].
ret = (length(tr, c[tr], p) * 1LL * siz[a[tr]]) % moder;
ret = mod_plus(ret, calc(a[tr], c[tr]));
ret = mod_plus(ret, calc(b[tr], p - ls));
}
return D[key] = ret;
} inline void solve() {
res[] = ;
for(LL i = ; i <= n; i++) {
res[i] = mod_plus(((siz[a[i]] % moder) * 1LL * (siz[b[i]] % moder) % moder * 1LL * l[i]) % moder, mod_plus(res[a[i]], res[b[i]]));
LL x = calc(a[i], c[i]);
LL y = calc(b[i], d[i]);
res[i] = mod_plus(mod_plus(res[i], (x * siz[b[i]]) % moder), (y * siz[a[i]]));
}
for(LL i = ; i <= n; i++)
printf(Auto"\n", res[i]);
} int main() {
freopen("zi.in", "r", stdin);
freopen("zi.out", "w", stdout);
init();
solve();
return ;
}
NOIP模拟题 2017.7.3 - 模拟 - 贪心 - 记忆化搜索的更多相关文章
- ACM International Collegiate Programming Contest, Tishreen Collegiate Programming Contest (2017)- K. Poor Ramzi -dp+记忆化搜索
ACM International Collegiate Programming Contest, Tishreen Collegiate Programming Contest (2017)- K. ...
- Codeforces Round #554 (Div. 2) D 贪心 + 记忆化搜索
https://codeforces.com/contest/1152/problem/D 题意 给你一个n代表合法括号序列的长度一半,一颗有所有合法括号序列构成的字典树上,选择最大的边集,边集的边没 ...
- Codeforces Round #536 E. Lunar New Year and Red Envelopes /// 贪心 记忆化搜索 multiset取最大项
题目大意: 给定n m k:(1≤n≤1e5, 0≤m≤200, 1≤k≤1e5) 表示n个时间长度内 最多被打扰m次 k个红包 接下来k行描述红包 s t d w:(1≤s≤t≤d≤n , 1≤w≤ ...
- [NOIP2010] 引水入城 贪心 + 记忆化搜索
---题面--- 题解: 本蒟蒻并没有想到bfs的做法,,,, 只会dfs了 首先我们需要知道一个性质. 我们设k[i].l 为在i点建立水库可以支援到的最左边的城市,k[i].r为最右边的. 那么点 ...
- 【GDOI2018模拟8】 数学竞赛 三角函数性质+记忆化搜索
数据范围:p,q≤20. 只能说我整个人傻逼了..... 我们考虑三角函数的部分性质: $sin(x)=\sqrt{ 1-cos^2(x)}$ $cos(x)=\sqrt{1-sin^2(x)}$ $ ...
- 2017广东工业大学程序设计竞赛决赛 题解&源码(A,数学解方程，B,贪心博弈，C,递归，D,水，E,贪心，面试题，F,贪心，枚举，LCA，G,dp，记忆化搜索，H,思维题)
心得: 这比赛真的是不要不要的,pending了一下午,也不知道对错,直接做过去就是了,也没有管太多! Problem A: 两只老虎 Description 来,我们先来放松下,听听儿歌,一起“唱” ...
- [CSP-S模拟测试]:集合合并（记忆化搜索）
题目传送门(内部题133) 输入格式 第一行一个正整数$n$. 第二行$n$个正整数$a_i$,表示一开始有$S_i=\{a_i\}$ 输出格式 输出一个非负整数表示最大的收益之和 样例 样例输入: ...
- [CSP-S模拟测试]:彩球问题（记忆化搜索）
题目传送门(内部题91) 输入格式 第一行一个正整数$N$,表示颜色种类数. 第二行$N$个正整数$k[i],k[i]$表示第$i$种颜色的数量$(1\leqslant k[i]\leqslant 3 ...
- 【蓝桥杯真题】地宫取宝(搜索->记忆化搜索详解)
链接 [蓝桥杯][2014年第五届真题]地宫取宝 题目描述 X 国王有一个地宫宝库.是 n x m 个格子的矩阵.每个格子放一件宝贝.每个宝贝贴着价值标签. 地宫的入口在左上角,出口在右下角. 小明被 ...
随机推荐
- Codeforces Round #439 (Div. 2)
A. The Artful Expedient 题目链接:http://codeforces.com/contest/869/problem/A 题目意思:给你两个数列,各包含n个数,现在让你从上下两 ...
- CCCC训练赛一些模板 struct sstream
重载与构造 struct node { friend bool operator< (node n1, node n2) { return n1.priority > n2.priorit ...
- logback多环境配置
现在项目基本都是要区分测试开发等等一系列环境的,也因此maven,spring之类的都具有profile这类功能,可以针对不同的环境采用不同的配置.因此日志也可能根据不同的环境需要不同的配置.恰巧手头 ...
- Python爬虫框架Scrapy实例（四）下载中间件设置
还是豆瓣top250爬虫的例子,添加下载中间件,主要是设置动态Uesr-Agent和代理IP Scrapy代理IP.Uesr-Agent的切换都是通过DOWNLOADER_MIDDLEWARES进行控 ...
- SQLSERVER 函数大全
转自:http://blog.csdn.net/travylee/article/details/7216481 SQL2008 表达式:是常量.变量.列或函数等与运算符的任意组合. 1. 字符串函数 ...
- wxWidgets与其他工具库的比较(上)
本文是在wxWidgets Wiki上面找到的一篇,对比了wxWidgets和其他一些界面工具的特点.看到很多朋友在网上询问这些库各自的特点,我想先把这篇文章翻译出来——毕竟这也算是一篇官方的文章,应 ...
- requests库的post请求
requests库的post请求 #coding:utf-8 import requests import json class Trans(object): def __init__(self, w ...
- Centos 集群配置SSH免登陆脚本
首先编写脚本生成集群服务器列表: hostsList.sh #!/bin/bash preIp="11.11.225." pwd="dyj2017" for i ...
- 【Cocos2dx 3.3 Lua】剪裁结点ClippingNode
参考资料: http://shahdza.blog.51cto.com/2410787/1561937 http://blog.csdn.net/jackystudio/article/det ...
- 配置apache实现对网站某一目录的访问自动跳转到指定目录
访问www.baidu.com/Hello目录,实际访问/new_balance/hello2 Alias /Hello/ /new_balance/hello2 <Directory /new ...