建模算法（十一）——目标规划

求解多目标规划的思路

1、加权系数法

为每一个目标加一个权系数，把多目标模型转化成单一目标模型。但是困难时确定合理的权系数，以反映不同目标之间的重要程度。

2、优先等级法

将各目标按其重要程度分为不同的优先等级，转化为单目标模型。

3、有效解法

寻求能够照顾到各个目标，并使决策者感到满意的解。由决策者来确定选取哪一个解，即得到满意的解。但是有效解太多，无法挑选

一、目标规划的数学模型

1、正、负偏差变量

2、绝对约束和目标约束

（1）绝对约束：一定要达到的要求，线性规划的约束条件都是

（2）软约束（目标约束）：就是在这个目标值允许有一定的正负偏差存在。

3、优先因子（优先等级）与权系数

一个规划问题如果有多个目标，可以按照重要性来规定一个优先因子P，越重要的越优先。

4、目标规划的目标函数

每一个目标值确定后，要求是尽可能小的缩小偏差。因此目标函数只能是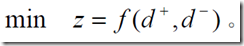，有三种形式

（1）要求恰好达到目标值，即正负偏差都要小

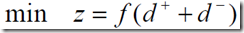
（2）要求不超过目标值，正偏差小

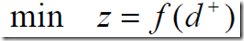
（3）要求超过目标值，负偏差小

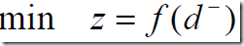
5、目标规划的一般数学模型

二、求解目标规划的序贯式模型

解题思路：

按照优先级的先后次序，将目标规划问题分解成一系列的单项目标规划问题。然后再依次求解。（由于使用LINGO求解，暂时忽略）

三、多目标规划的MATLAB解法

1、一般模型

2、MATLAB封装的函数

[x,fval]=fgoalattain('fun',x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon)

（1）fun是用M文件定义的目标向量函数

（2）x0是初值，一般弄个随机列向量

（3）weight为权重，一般为goal的绝对值

（4）A，b定义不等式约束A*x<=b,Aeq,beq定义等式约束

（5）nonlcon是用M文件定义的非线性约束条件c(x)<=0，ceq(x)=0

（6）返回值，x是最优解，fval是最优值

3、例子

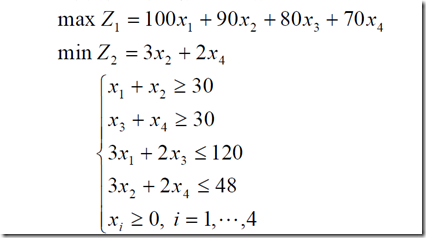
function F=Fun(x)
F(1)=-100*x(1)-90*x(2)-80*x(3)-70*x(4);
F(2)=3*x(2)+2*x(4);

a=[-1  -1  0  0
    0  0  -1  -1
    3  0  2  0
    0  3  0  2];
b=[-30  -30  120  48]';
c1=[-100  -90  -80  -70];
c2=[0  3  0 2 ];

[x1,g1]=linprog(c1,a,b,[],[],zeros(4,1))
[x2,g2]=linprog(c2,a,b,[],[],zeros(4,1))

g3=[g1;g2];
[x,fval]=fgoalattain('Fun',rand(4,1),g3,abs(g3),a,b,[],[],zeros(4,1));