题解【洛谷P1038/CJOJ1707】[NOIP2003提高组]神经网络

Description

问题背景：
人工神经网络（ Artificial Neural Network ）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同 学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

问题描述：
在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经 元之间至多有一条边相连，下图是一个神经元的例子：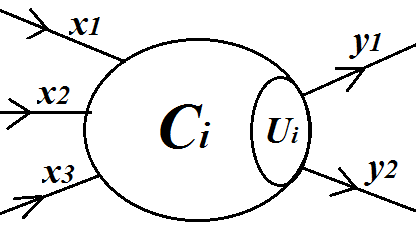

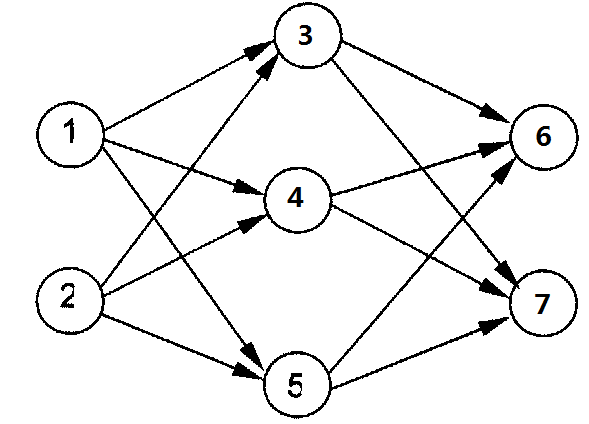
神经元（编号为 1 ） 图 中， X1—X3 是信息输入渠道， Y1 － Y2 是信息输出渠道， C i 表示神经元目前的状态， U i 是阈值，可视为神经元的一个内在参数。神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经元分为几层；称为输入层、输出层， 和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

兰兰规定， C i 服从公式：（其中 n 是网络中所有神经元的数目）

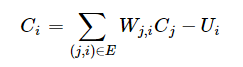
公 式中的 W ji （可能为负值）表示连接 j 号神经元和 i 号神经元的边的权值。当 C i 大于 0 时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为 C i 。如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（ C i ），要求你的程序运算出最后网络输出层的状态。

Input

输入第一行是两个整 数 n （ 1≤n≤200 ）和 p 。接下来 n 行，每行两个整数，第 i ＋ 1 行是神经元 i 最初状态和其阈值（ U i ），非输入层的神经元开始时状态必然为 0 。再下面 P 行，每行由两个整数 i ， j 及一个整数 W ij ，表示连接神经元 i 、 j 的边权值为 W ij 。

Output

输出包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。 仅输出最后状态非零的输出层神经元状态，并且按照编号由小到大顺序输出！若输出层的神经元最后状态均为 0 ，则输出 NULL 。

Sample Input

5 6 
1 0 
1 0 
0 1 
0 1 
0 1 
1 3 1 
1 4 1 
1 5 1 
2 3 1 
2 4 1 
2 5 1

Sample Output

3 1 
4 1 
5 1

Source

NOIP2003
图论 ，递推 ， 拓扑排序 ，搜索， 模拟

Solution

本题是拓扑排序模板题。

由于1≤n≤100（CJOJ上n≤200），因此可以用邻接矩阵存图。

最后，注意输出的判断，就可以AC这道题了！

Code

 #include <bits/stdc++.h>

 using namespace std;

 inline int read()//快速读入
 {
     int f=,x=;
     char c=getchar();

     while(c<'' || c>'')
     {
         if(c=='-')f=-;
         c=getchar();
     }

     while(c>='' && c<='')
     {
         x=x*+c-'';
         c=getchar();
     }

     return f*x;
 }

 int fl,n,m,p,c[],u[],r[],o[],q[][],t[],tail,head;

 int main()
 {
     n=read(),p=read();

     for(register int i=; i<=n; i++)
     {
         c[i]=read(),u[i]=read();

         if(c[i]!=)//第一层的直接加入队列
         {
             t[++tail]=i;
         }
         else
         {
             c[i]=c[i]-u[i];//其它层数可以直接减去u[i]
         }
     }

     for(register int i=; i<=p; i++)
     {
         int x=read(),y=read(),w=read();

         q[x][y]=w;//邻接矩阵存图

         ++r[y],++o[x];//记录入度和出度
     }

     for(register int i=; i<=n; i++)
     {
         if(r[i]==)
         {
             t[++tail]=i;//将入度为0的点加入队列
         }
     }

     while(head<tail)//拓扑排序
     {
         ++head;

         if(c[t[head]]>)
         {
             for(register int i=; i<=n; i++)
             {
                 if(q[t[head]][i]!=)//如果当前节点与节点i有边
                 {
                     c[i]=c[i]+q[t[head]][i]*c[t[head]];//利用公式计算

                     t[++tail]=i;//加入队列
                 }
             }

             if(o[t[head]]!=)//除了最后一层都要将最初状态清零
             {
                 c[t[head]]=;
             }
         }
     }

     for(register int i=; i<=n; i++)//输出
     {
         if(c[i]>)//如果状态大于0
         {
             printf("%d %d\n",i,c[i]);//输出

             fl=;//标记有解
         }
     }

     if(!fl)//输出无解
     {
         printf("NULL");
     }

     return ;//结束
 }