两种常见的缓存淘汰算法LFU&LRU

1. LFU

1.1. 原理

LFU（Least Frequently Used）算法根据数据的历史访问频率来淘汰数据，其核心思想是“如果数据过去被访问多次，那么将来被访问的频率也更高”。

1.2. 实现

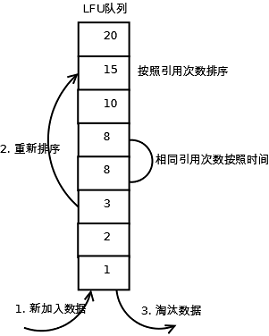
LFU的每个数据块都有一个引用计数，所有数据块按照引用计数排序，具有相同引用计数的数据块则按照时间排序。

具体实现如下：

1. 新加入数据插入到队列尾部（因为引用计数为1）；

2. 队列中的数据被访问后，引用计数增加，队列重新排序；

3. 当需要淘汰数据时，将已经排序的列表最后的数据块删除。

1.3. 分析

l 命中率

一般情况下，LFU效率要优于LRU，且能够避免周期性或者偶发性的操作导致缓存命中率下降的问题。但LFU需要记录数据的历史访问记录，一旦数据访问模式改变，LFU需要更长时间来适用新的访问模式，即：LFU存在历史数据影响将来数据的“缓存污染”效用。

l 复杂度

需要维护一个队列记录所有数据的访问记录，每个数据都需要维护引用计数。

l 代价

需要记录所有数据的访问记录，内存消耗较高；需要基于引用计数排序，性能消耗较高。

2. LRU
2.1. 原理

LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”。

2.2. 实现

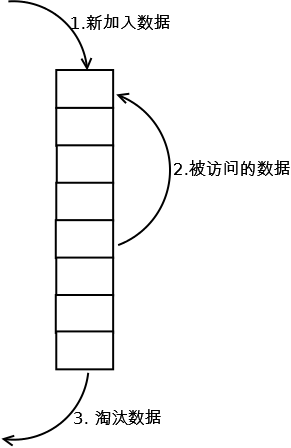
最常见的实现是使用一个链表保存缓存数据，详细算法实现如下：

1. 新数据插入到链表头部；

2. 每当缓存命中（即缓存数据被访问），则将数据移到链表头部；

3. 当链表满的时候，将链表尾部的数据丢弃。

2.3. 分析

【命中率】

当存在热点数据时，LRU的效率很好，但偶发性的、周期性的批量操作会导致LRU命中率急剧下降，缓存污染情况比较严重。

【复杂度】

实现简单。

【代价】

命中时需要遍历链表，找到命中的数据块索引，然后需要将数据移到头部。

3. LRU-K

3.1. 原理

LRU-K中的K代表最近使用的次数，因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题，其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。

3.2. 实现

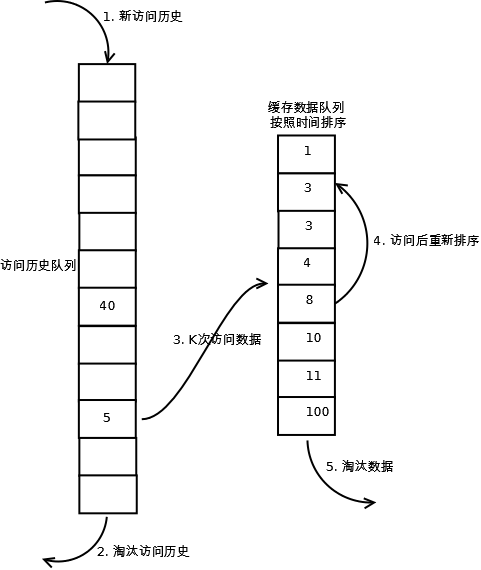
相比LRU，LRU-K需要多维护一个队列，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候，才将数据放入缓存。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下：

1. 数据第一次被访问，加入到访问历史列表；

2. 如果数据在访问历史列表里后没有达到K次访问，则按照一定规则（FIFO，LRU）淘汰；

3. 当访问历史队列中的数据访问次数达到K次后，将数据索引从历史队列删除，将数据移到缓存队列中，并缓存此数据，缓存队列重新按照时间排序；

4. 缓存数据队列中被再次访问后，重新排序；

5. 需要淘汰数据时，淘汰缓存队列中排在末尾的数据，即：淘汰“倒数第K次访问离现在最久”的数据。

LRU-K具有LRU的优点，同时能够避免LRU的缺点，实际应用中LRU-2是综合各种因素后最优的选择，LRU-3或者更大的K值命中率会高，但适应性差，需要大量的数据访问才能将历史访问记录清除掉。

3.3. 分析

【命中率】

LRU-K降低了“缓存污染”带来的问题，命中率比LRU要高。

【复杂度】

LRU-K队列是一个优先级队列，算法复杂度和代价比较高。

【代价】

由于LRU-K还需要记录那些被访问过、但还没有放入缓存的对象，因此内存消耗会比LRU要多；当数据量很大的时候，内存消耗会比较可观。

LRU-K需要基于时间进行排序（可以需要淘汰时再排序，也可以即时排序），CPU消耗比LRU要高。