神经网络优化篇：详解局部最优的问题(The problem of local optima)

局部最优的问题

在深度学习研究早期，人们总是担心优化算法会困在极差的局部最优，不过随着深度学习理论不断发展，对局部最优的理解也发生了改变。向展示一下现在怎么看待局部最优以及深度学习中的优化问题。

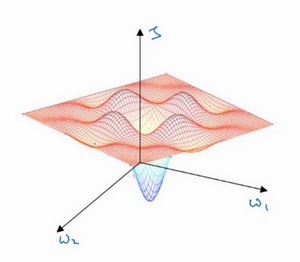
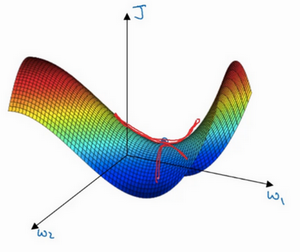
这是曾经人们在想到局部最优时脑海里会出现的图，也许想优化一些参数，把它们称之为\(W_{1}\)和\(W_{2}\)，平面的高度就是损失函数。在图中似乎各处都分布着局部最优。梯度下降法或者某个算法可能困在一个局部最优中，而不会抵达全局最优。如果要作图计算一个数字，比如说这两个维度，就容易出现有多个不同局部最优的图，而这些低维的图曾经影响了的理解，但是这些理解并不正确。事实上，如果要创建一个神经网络，通常梯度为零的点并不是这个图中的局部最优点，实际上成本函数的零梯度点，通常是鞍点。

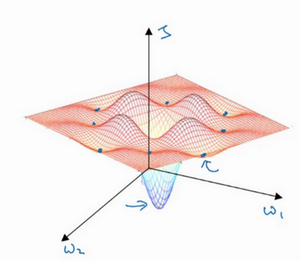
也就是在这个点，这里是\(W_{1}\)和\(W_{2}\)，高度即成本函数\(J\)的值。

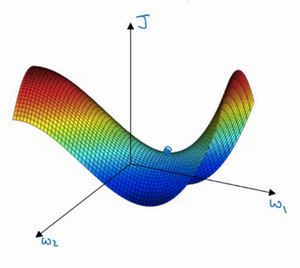
但是一个具有高维度空间的函数，如果梯度为0，那么在每个方向，它可能是凸函数，也可能是凹函数。如果在2万维空间中，那么想要得到局部最优，所有的2万个方向都需要是这样，但发生的机率也许很小，也许是\(2^{-20000}\)，更有可能遇到有些方向的曲线会这样向上弯曲，另一些方向曲线向下弯，而不是所有的都向上弯曲，因此在高维度空间，更可能碰到鞍点。

就像下面的这种：

而不会碰到局部最优。至于为什么会把一个曲面叫做鞍点，想象一下，就像是放在马背上的马鞍一样，如果这是马，这是马的头，这就是马的眼睛，画得不好请多包涵，然后就是骑马的人，要坐在马鞍上，因此这里的这个点，导数为0的点，这个点叫做鞍点。想那确实是坐在马鞍上的那个点，而这里导数为0。

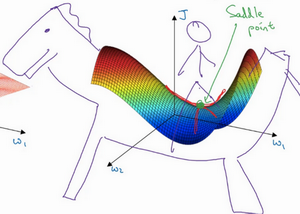
所以从深度学习历史中学到的一课就是，对低维度空间的大部分直觉，比如可以画出上面的图，并不能应用到高维度空间中。适用于其它算法，因为如果有2万个参数，那么\(J\)函数有2万个维度向量，更可能遇到鞍点，而不是局部最优点。

如果局部最优不是问题，那么问题是什么？结果是平稳段会减缓学习，平稳段是一块区域，其中导数长时间接近于0，如果在此处，梯度会从曲面从从上向下下降，因为梯度等于或接近0，曲面很平坦，得花上很长时间慢慢抵达平稳段的这个点，因为左边或右边的随机扰动。

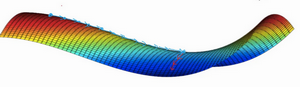
可以沿着这段长坡走，直到这里，然后走出平稳段。

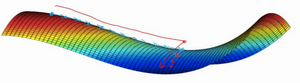
所以此篇博客的要点是，首先，不太可能困在极差的局部最优中，条件是在训练较大的神经网络，存在大量参数，并且成本函数\(J\)被定义在较高的维度空间。

第二点，平稳段是一个问题，这样使得学习十分缓慢，这也是像Momentum或是RMSprop，Adam这样的算法，能够加速学习算法的地方。在这些情况下，更成熟的优化算法，如Adam算法，能够加快速度，让尽早往下走出平稳段。

因为的网络要解决优化问题，说实话，要面临如此之高的维度空间，觉得没有人有那么好的直觉，知道这些空间长什么样，而且对它们的理解还在不断发展，不过希望这一点能够让更好地理解优化算法所面临的问题。