合并区间（区间排序，vector的动态扩容的应用）

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 104
• intervals[i].length == 2
• 0 <= starti <= endi <= 104

思路

关键点1：对小区间进行排序

首先要按照intervals中每个小区间的左边界进行排序

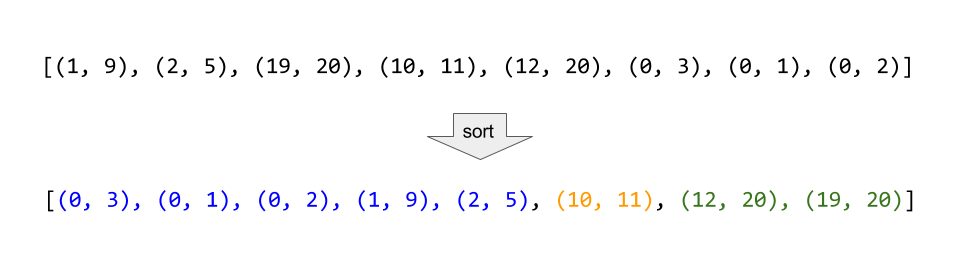
排序玩之后，如果某几个区间时可以合并的，那么这些区间一定是相邻的。如蓝色、黄色和绿色的区间分别可以合并成一个大区间。

之后我们需要遍历intervals，处理每个小区间的合并

关键点2：使用vector来存储合并后的结果，设为res

这里不要使用数组来放，因为数组没办法动态扩容，处理第一个放入的区间比较麻烦

遍历intervals

如果当前res为空，先直接将遍历所得区间加入

然后我们只需要每次取res的最后一个元素（也是一个小区间）的右区间，然后与当前遍历所得区间的左区间进行比较即可

如果当前遍历元素的左区间大于res最后一个元素的右区间，那么当前遍历得到的区间可以直接加入res中；

（相当于遇到了图中不同颜色的区间）

否则就更新当前res最后一个元素的右区间，取较大的那一个

代码

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        //关键点1：排序
        //首先要将所有区间按照区间的左边界进行排序，如果区间可以合并，那么这些区间一定是连续的
        //关键点2：使用vector存放区间
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> res;
        for(int i = 0; i < intervals.size(); ++i){
            //取当前遍历区间的左右边界
            int left = intervals[i][0], right = intervals[i][1];
            //注意还要考虑res为空的情况，如果为空也要直接将当前遍历值加入
            if(!res.size() || res.back()[1] < left) res.push_back(intervals[i]);
            else res.back()[1] = max(res.back()[1], right);
        }
        return res;
    }
};