Java使用joml计算机图形学库，将3D坐标旋转正交投影转为2D坐标

最近遇到了一个困扰我许久的难题，现将解决方案分享出来

由于我们的项目侧重点在前端绘图，导致了前后端工作量不协调，我后端接口很快就能写完，而前端一个图要画好久，领导见状将前端的任务分到后端一部分用Java代码来实现，然后给前端提供接口

而我接到的任务就是将Echarts中绘制三维图形的点旋转后投影为2D坐标，当我一个大专生在了解需求，并知道这涉及到线性代数和计算机图形学后，我的想法是这样的：

我想了很多种方法，一开始在网上搜Java相关资料，但是网上好像没有人处理过这种情况，找到的帖子都是做Java图形化的，他们所谓的坐标旋转是直接用眼球看到的界面效果，跟我想要的计算完全不同

而后我又拜托ChatGPT帮我写了几版，不得不说的确帮我写出来了，而且自己测试效果还可以，但是前端调接口后点数太多了，旋转后的坐标直接乱了，最终我在网上游荡了很久找到了解决方案，目前效果还算不错

功能实现

首先在pom.xml中添加joml的Maven坐标，该库是一个轻量级数学库，专门用于处理3D图形的数学计算

<!-- 计算机图形学计算库 -->

<dependency>

    <groupId>org.joml</groupId>

    <artifactId>joml</artifactId>

    <version>1.10.5</version>

</dependency>

然后创建个主类编写测试代码，方法很简单直接调用就好啦

import org.joml.Matrix3d;

import org.joml.Vector3d;

public class Application {

    public static void main(String[] args) {

        // 构建一个X轴旋转90°的旋转对象

        Matrix3d matrix = new Matrix3d().rotateX(Math.toRadians(90));

        // 构建一个3D坐标点

        Vector3d point = new Vector3d(10, 10, 10);

        // 执行旋转

        Vector3d transform = matrix.transform(point);

        // 打印旋转后的角度

        System.out.println(transform.x);

        System.out.println(transform.y);

        System.out.println(transform.z);

    }

}

很悲哀，这么简单的几行代码困扰了我两三天才把功能做出来，见识少就是不行啊

封装为Springboot接口

这里我就不写封装接口的过程了，我会把代码地址放到文章结尾，有需要请自行获取，这里展示一下接口的使用和效果

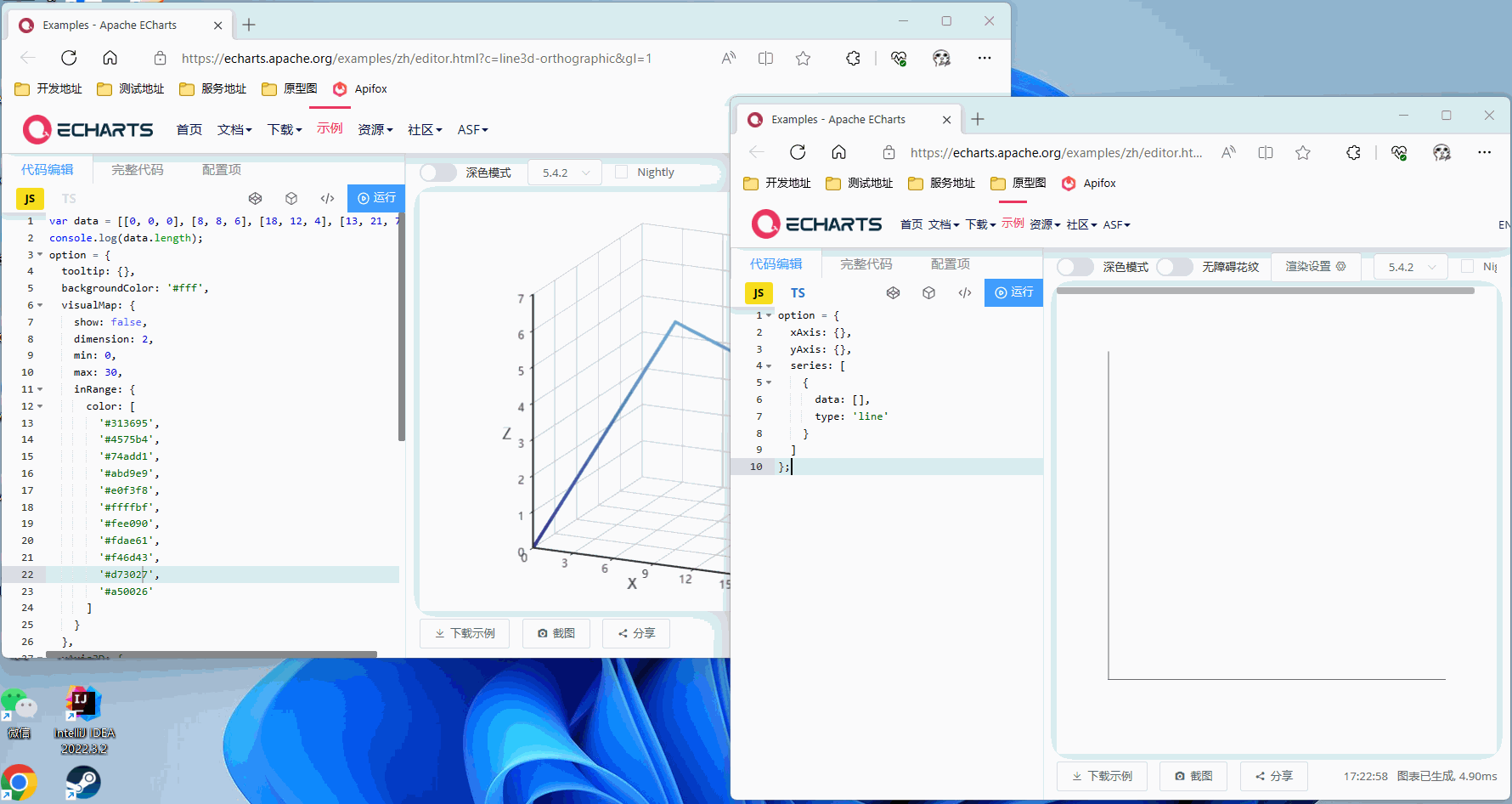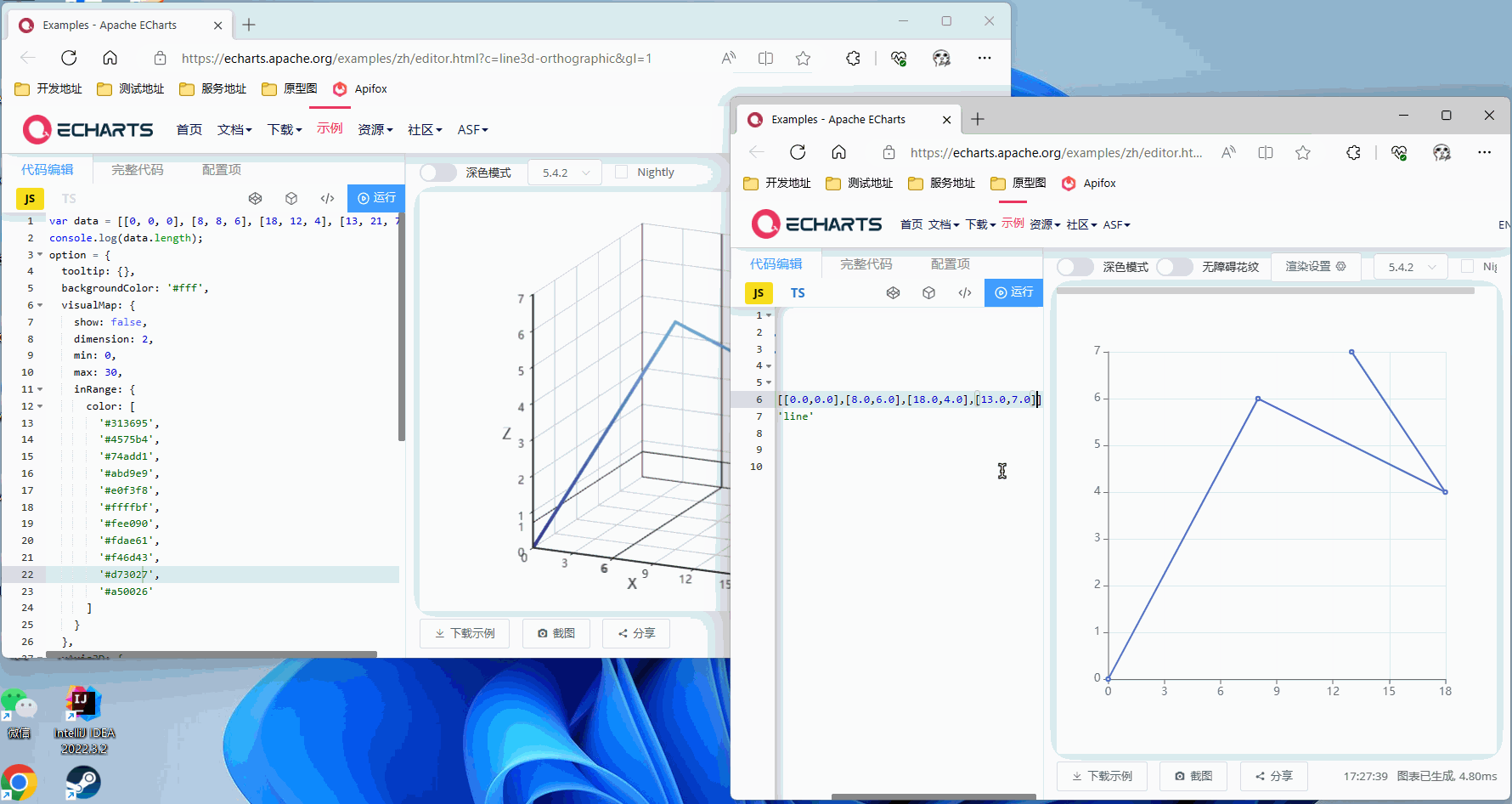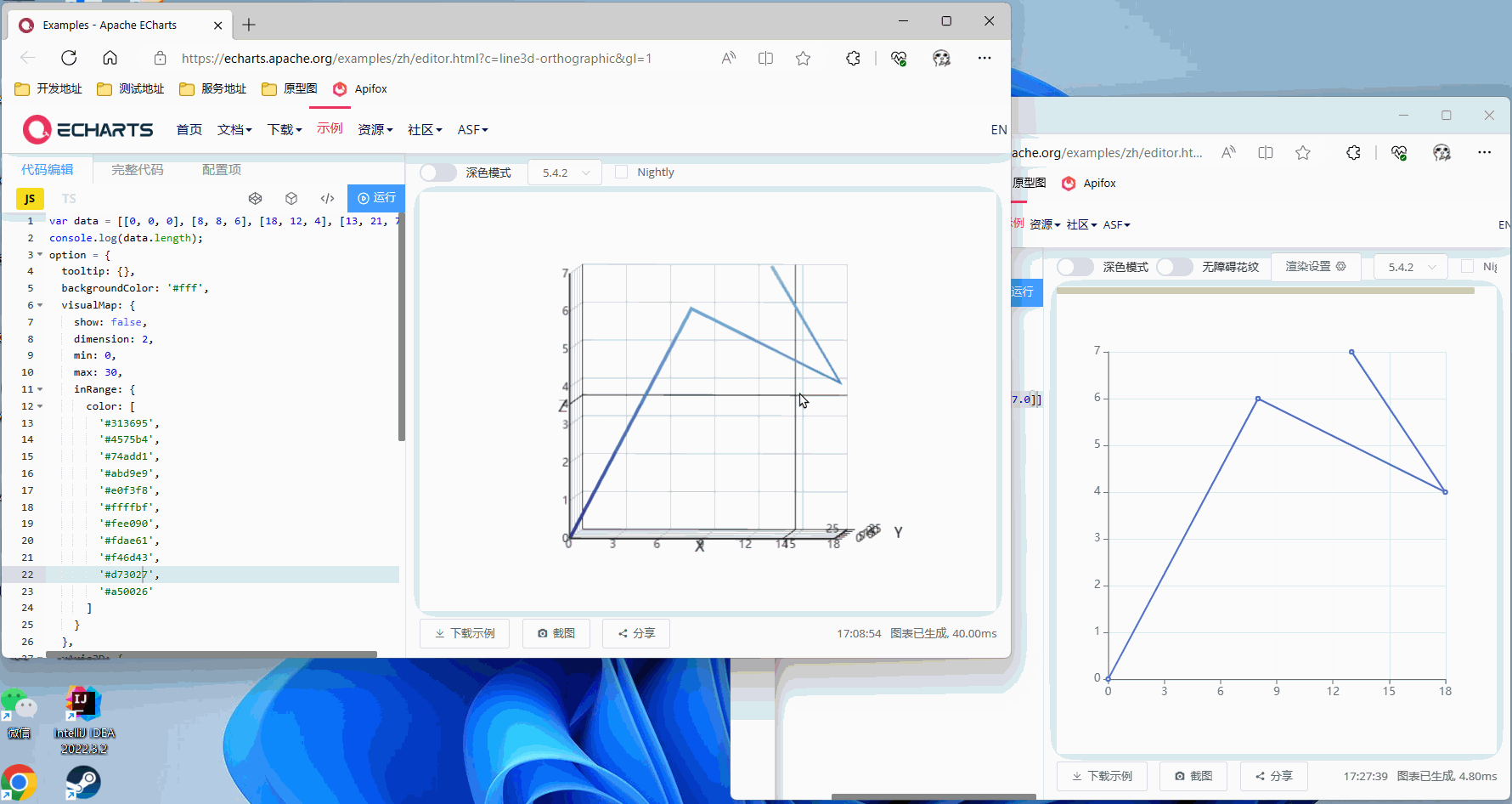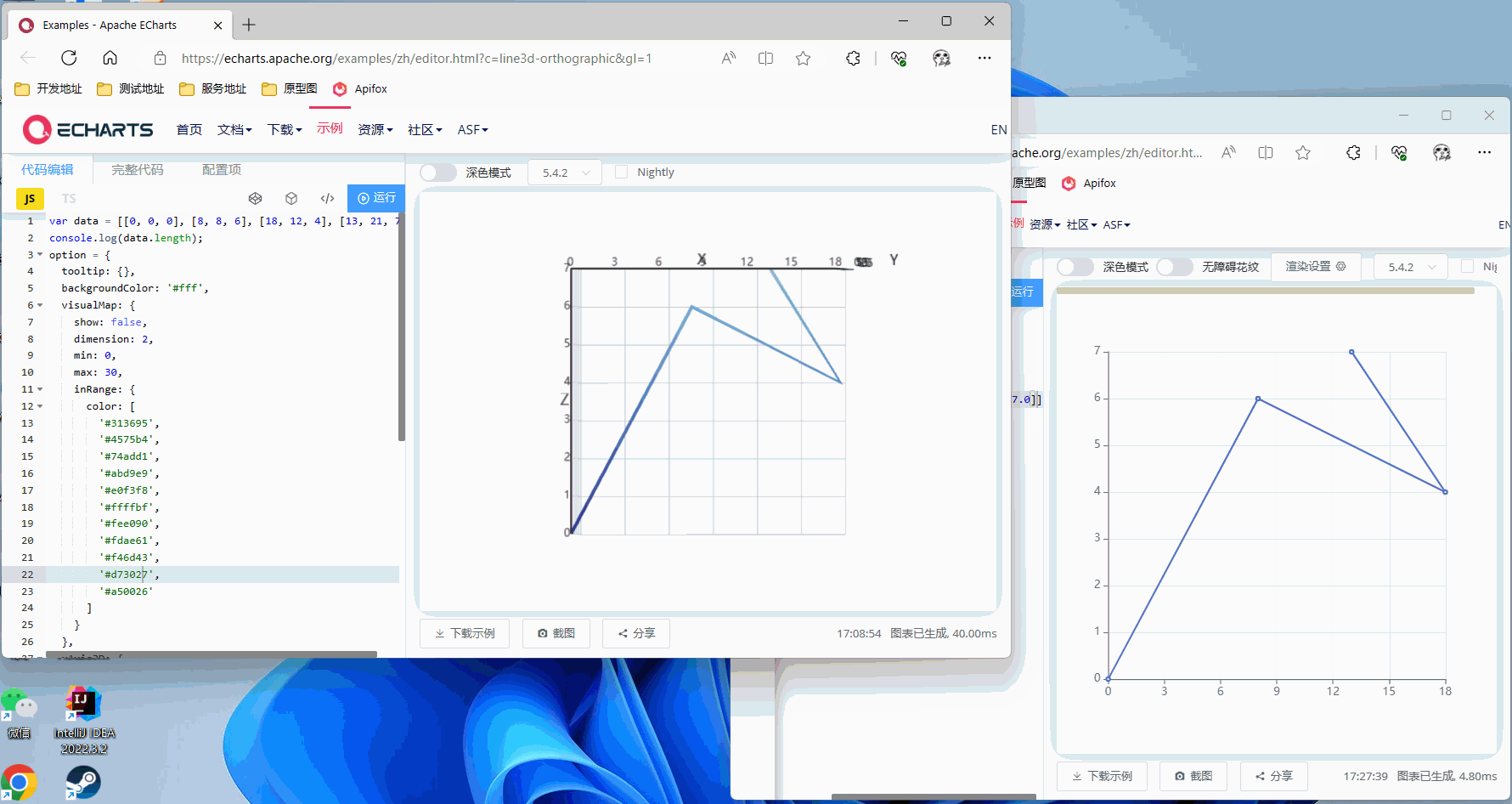
首先打开Echarts的官网，分别打开三维折线图和二维折线图，用我给的这组测试数据画出一个三维折线图，或者自己有测试数据也可以

var data = [[0, 0, 0], [8, 8, 6], [18, 12, 4], [13, 21, 7]];

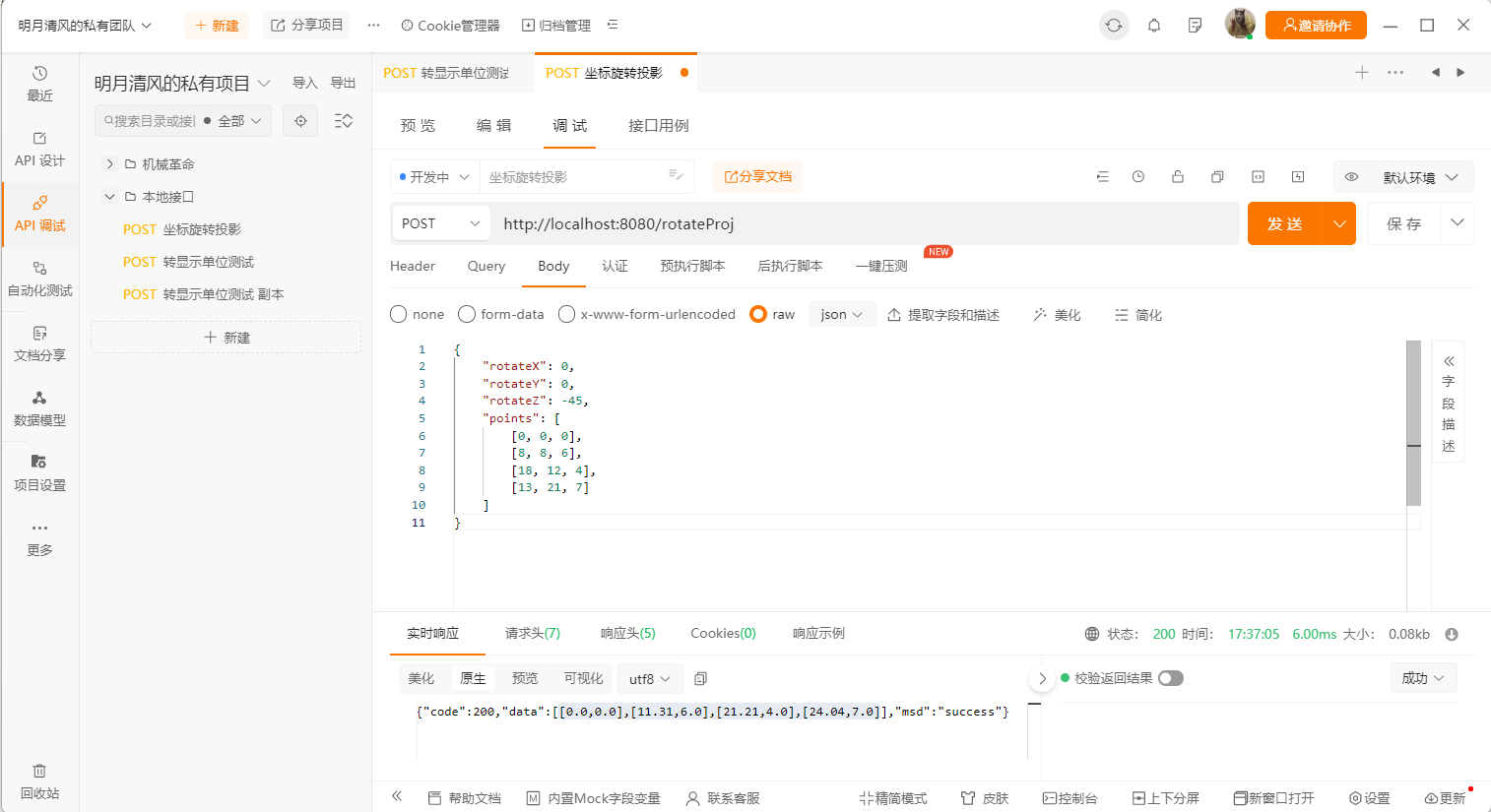
然后调用写好的rotateProj接口，将坐标和轴旋转角度传入，查看效果

不进行旋转，直接看正面

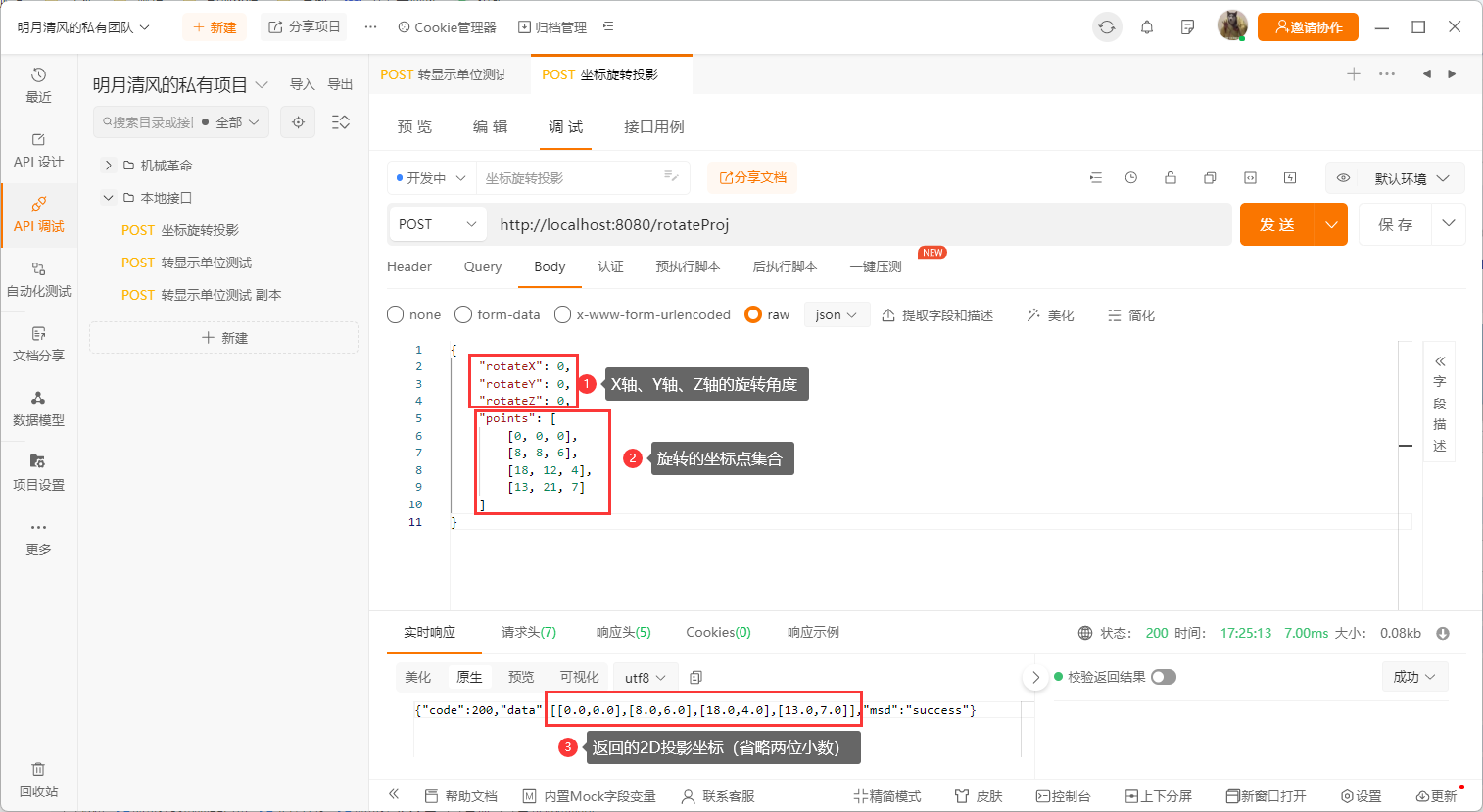
Z轴旋转90°

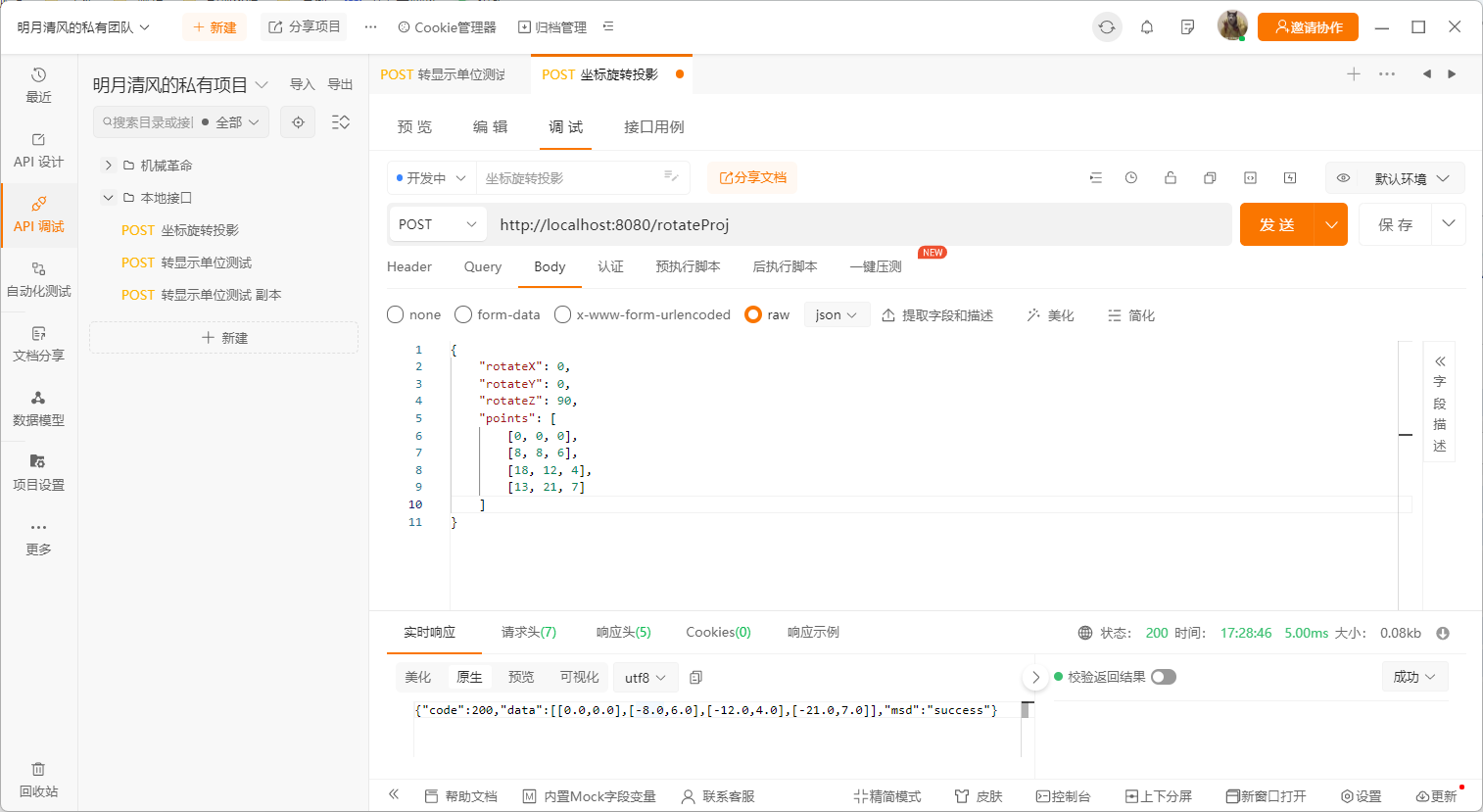
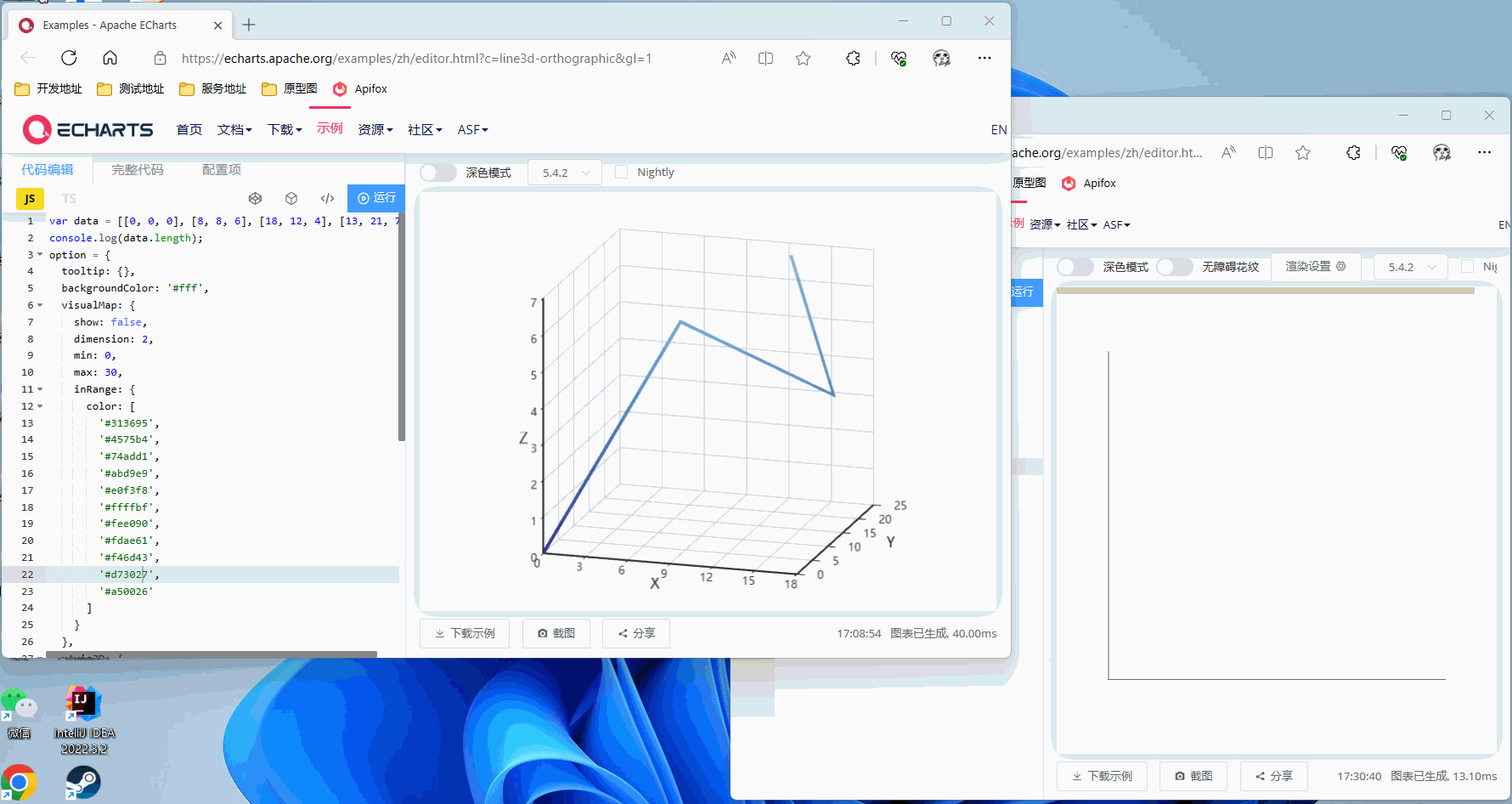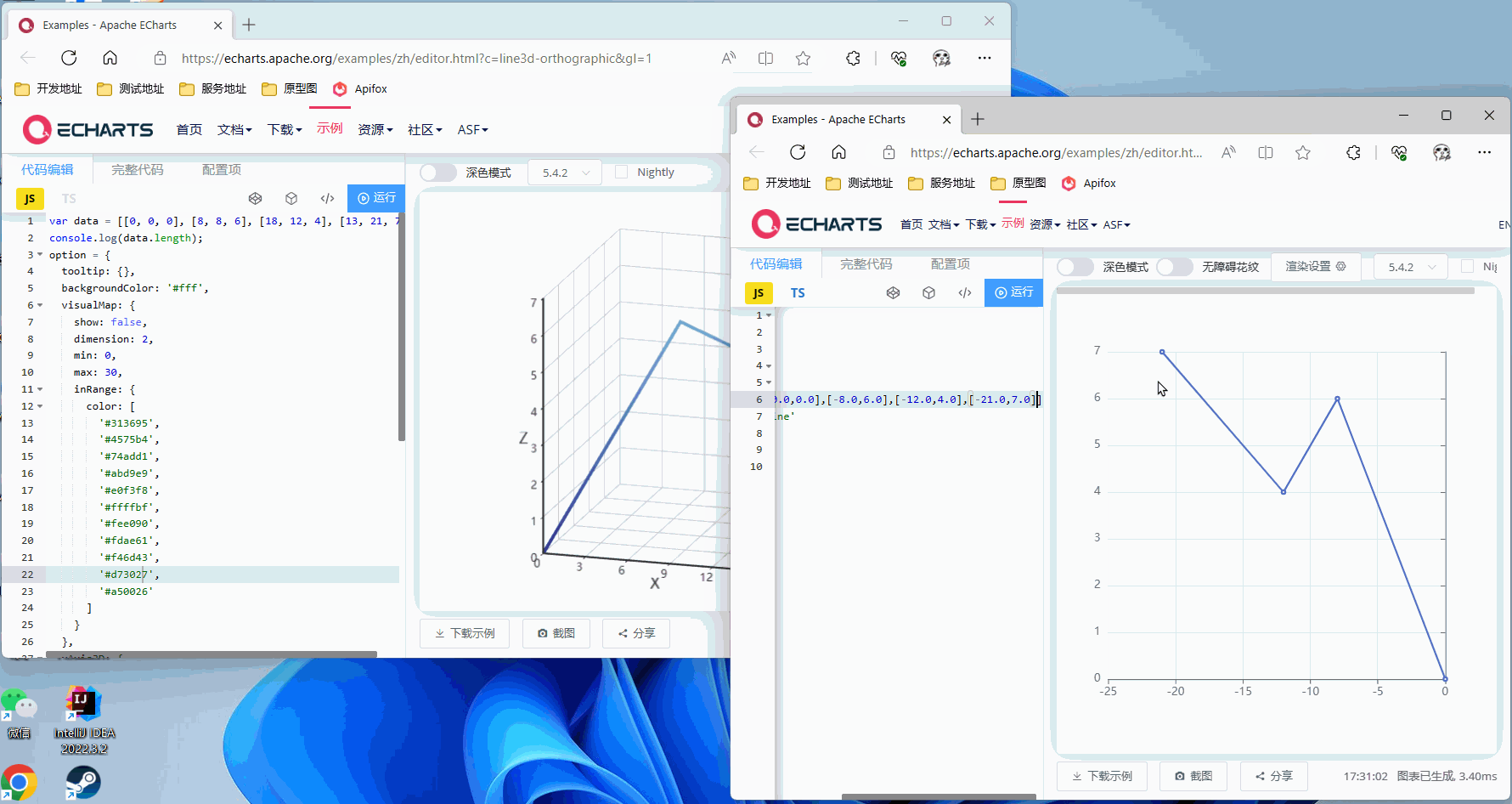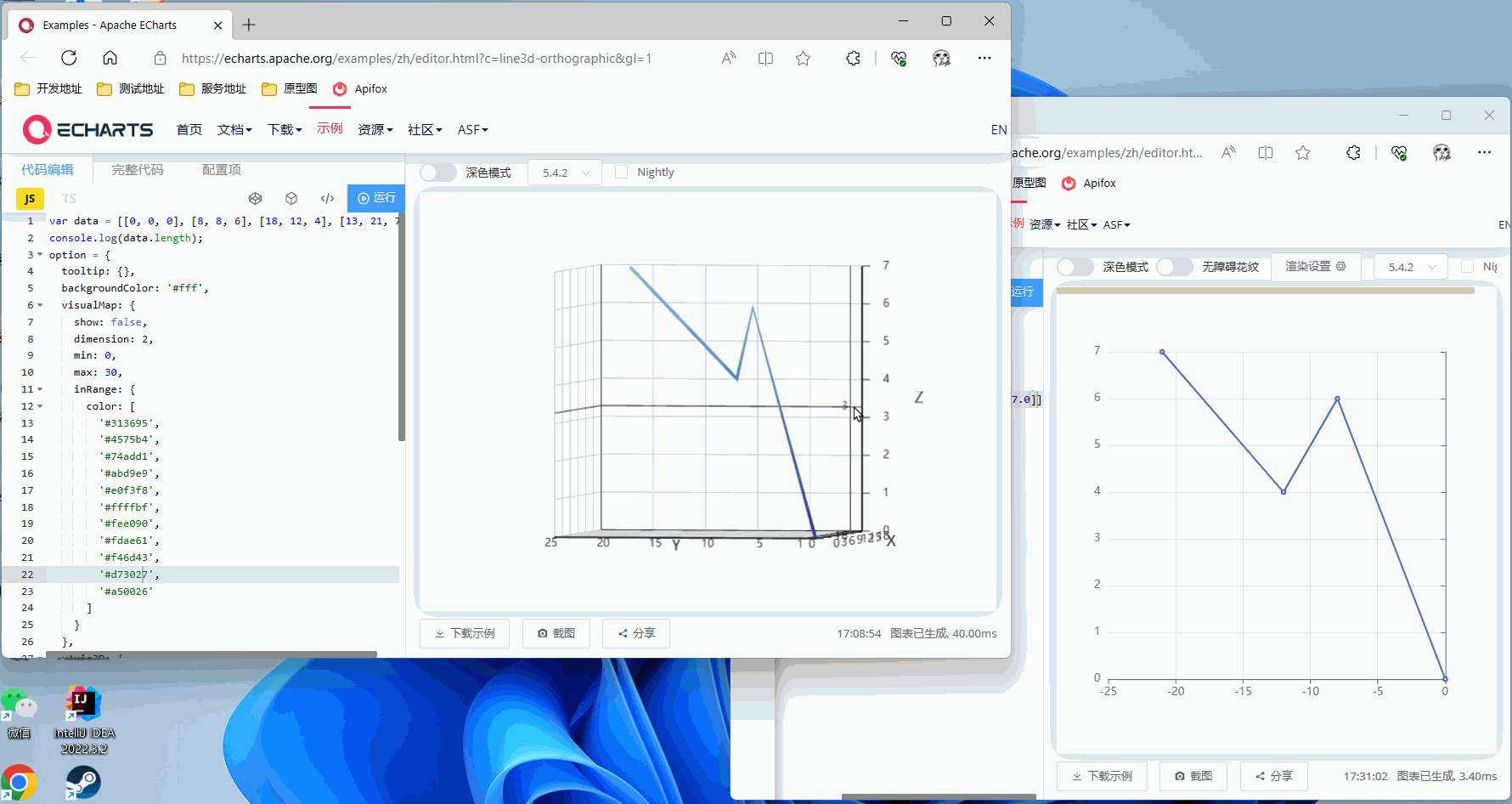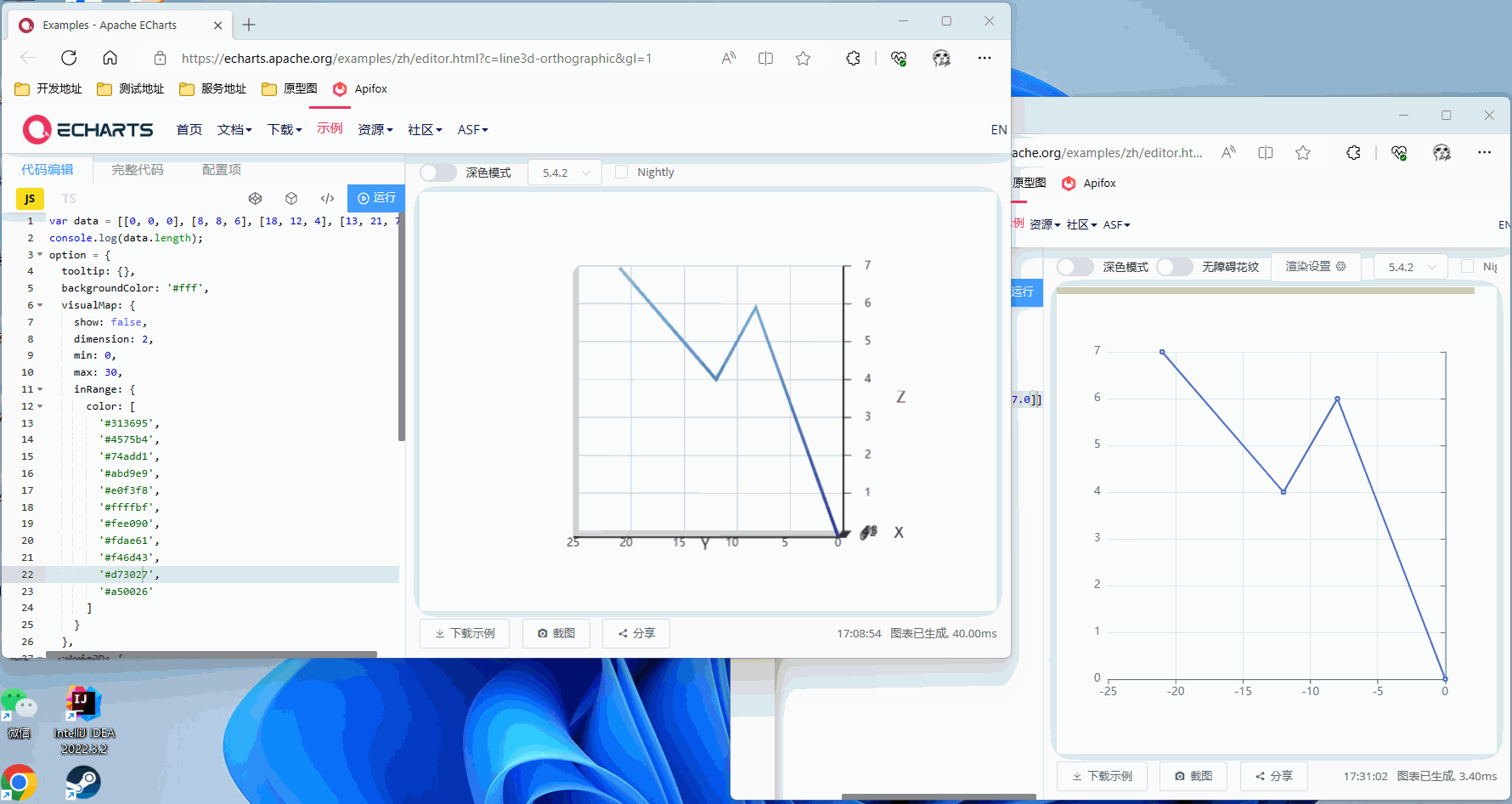
X轴旋转90°

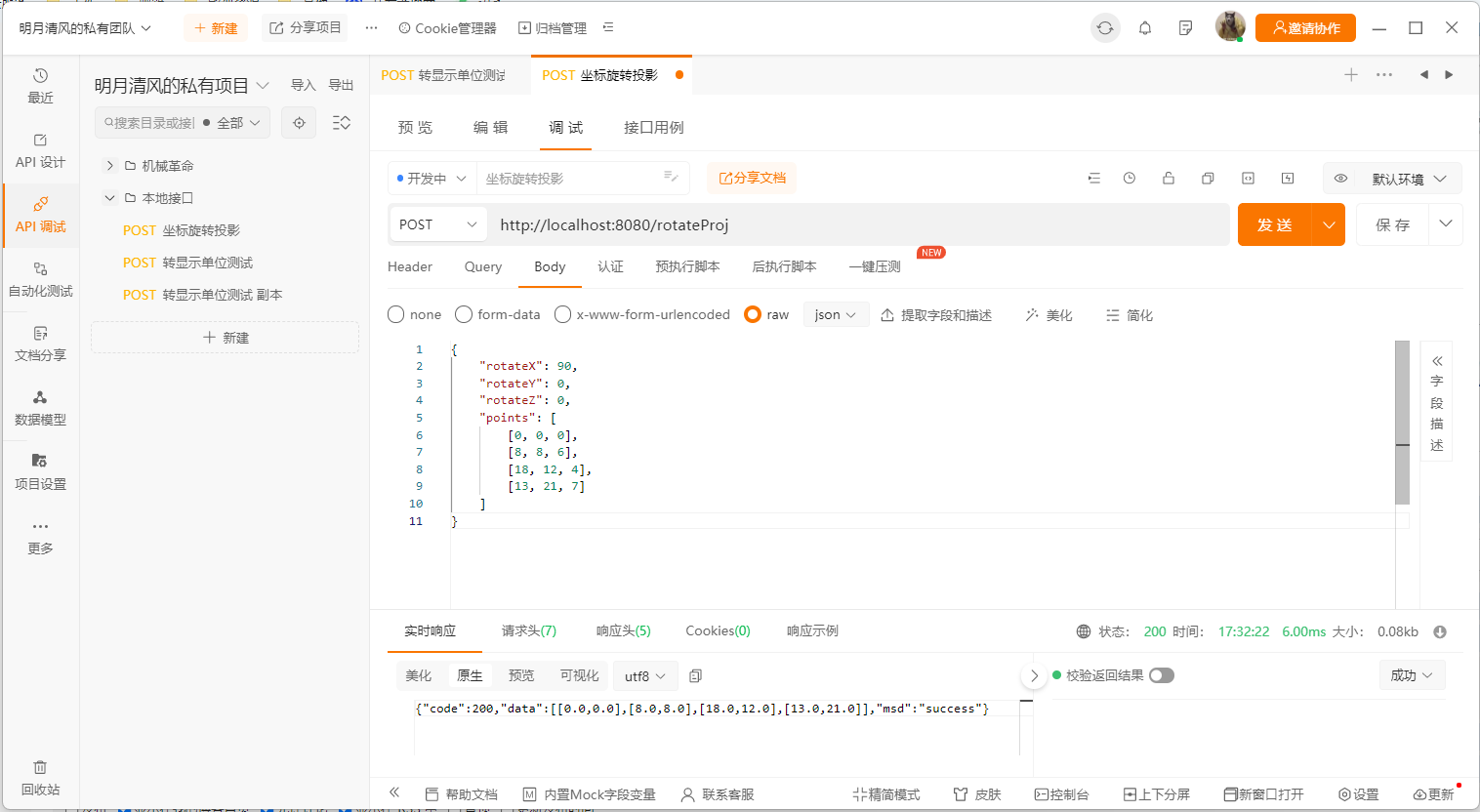
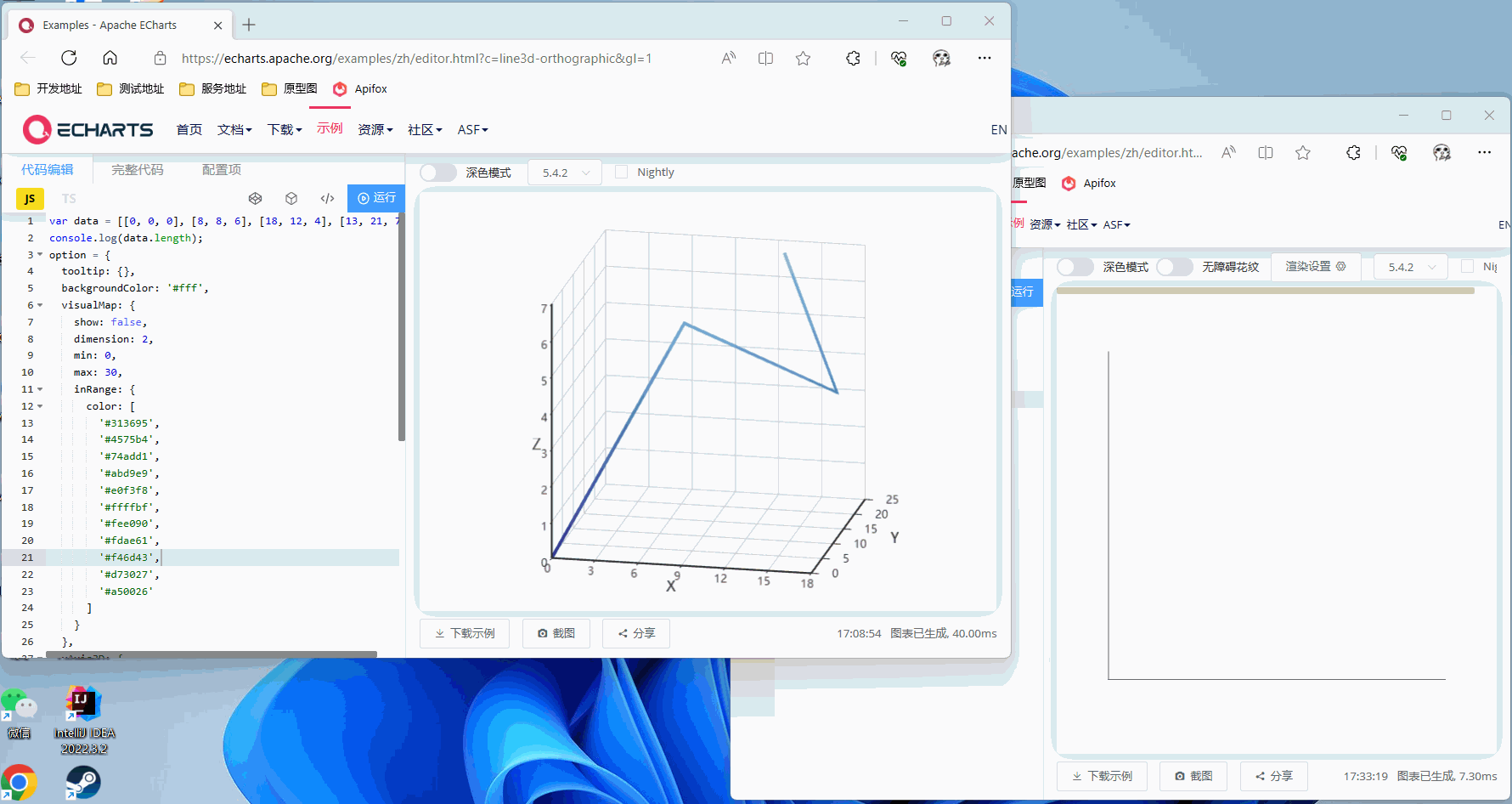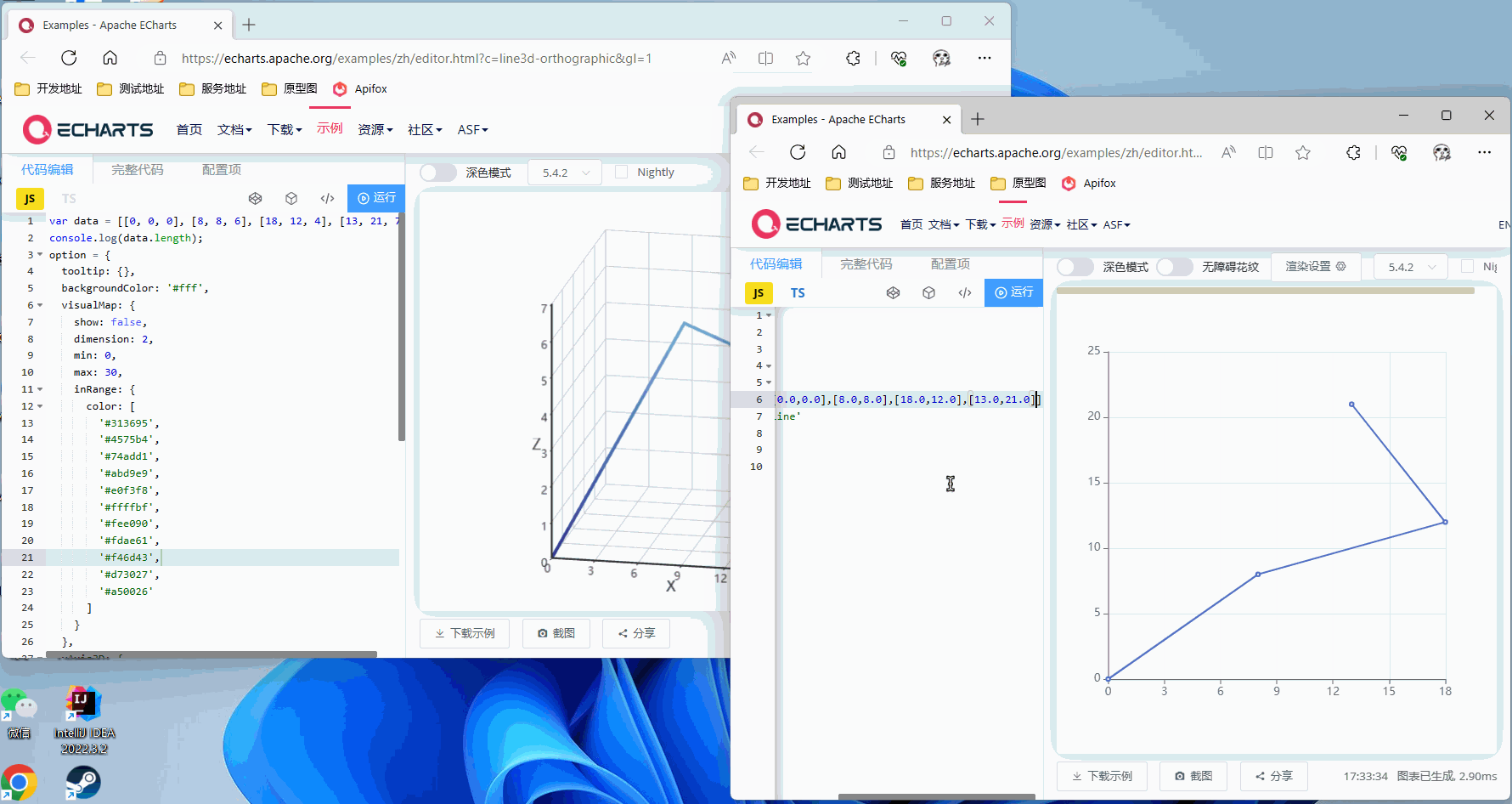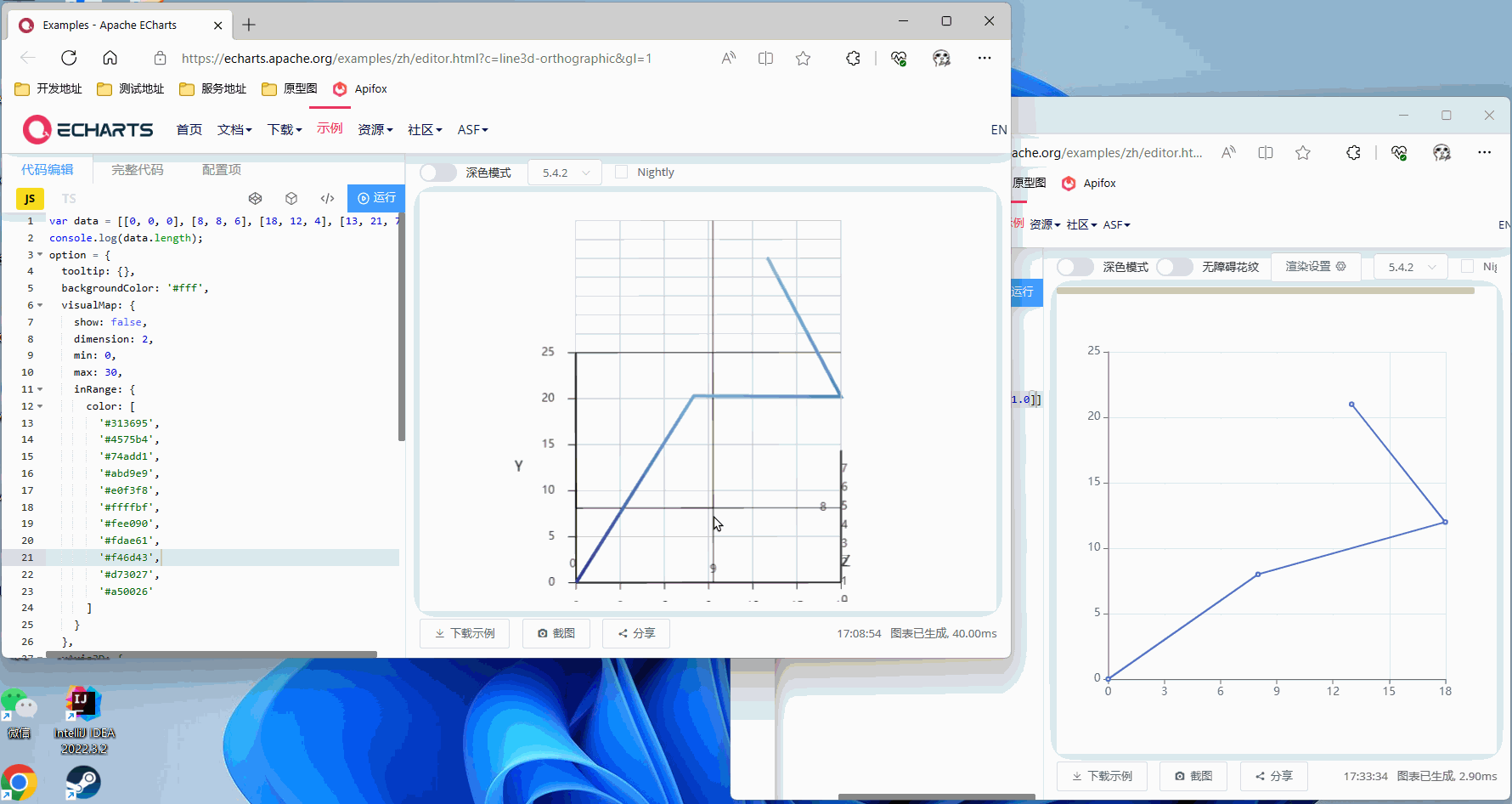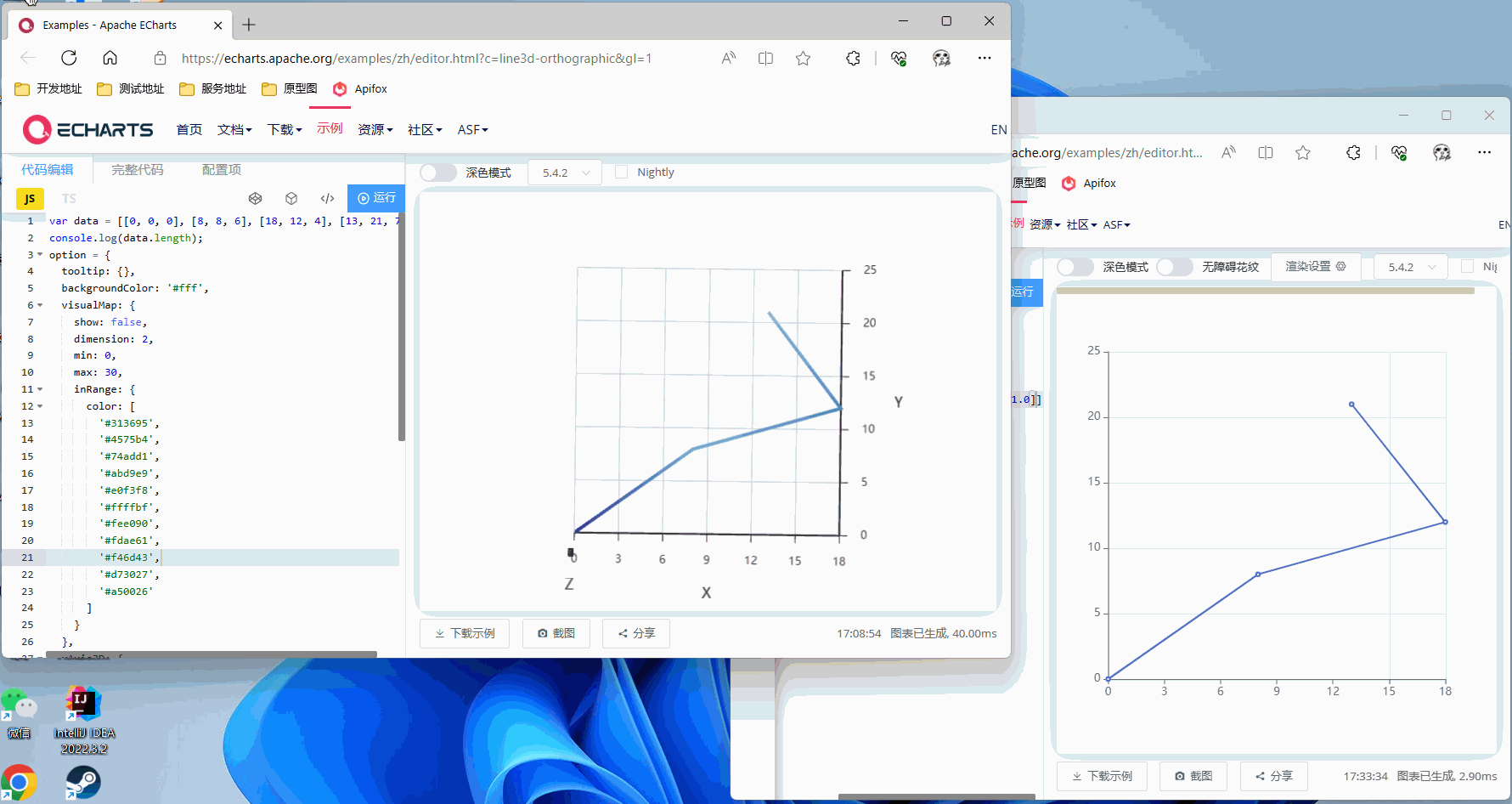
Z轴旋转45°

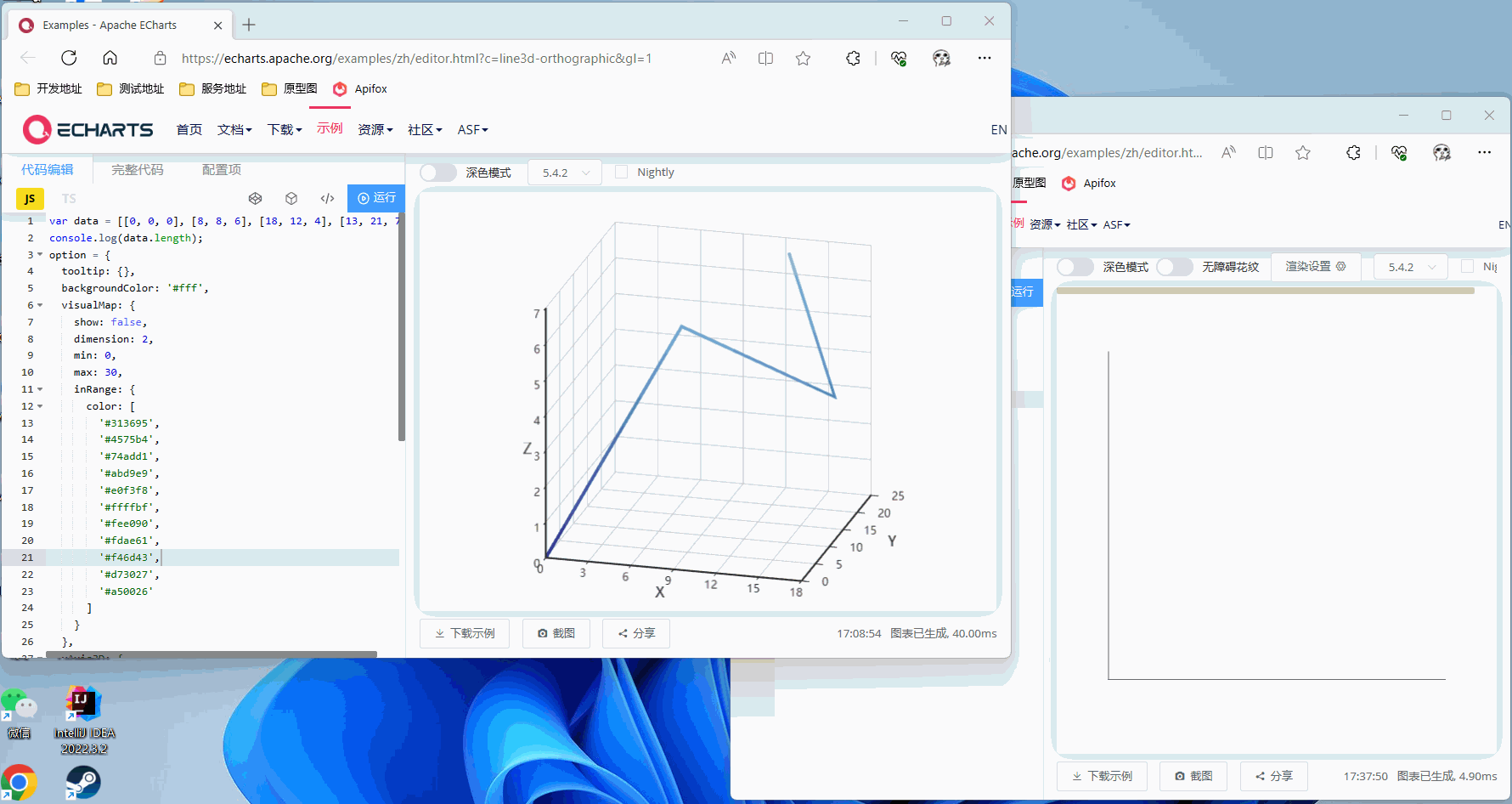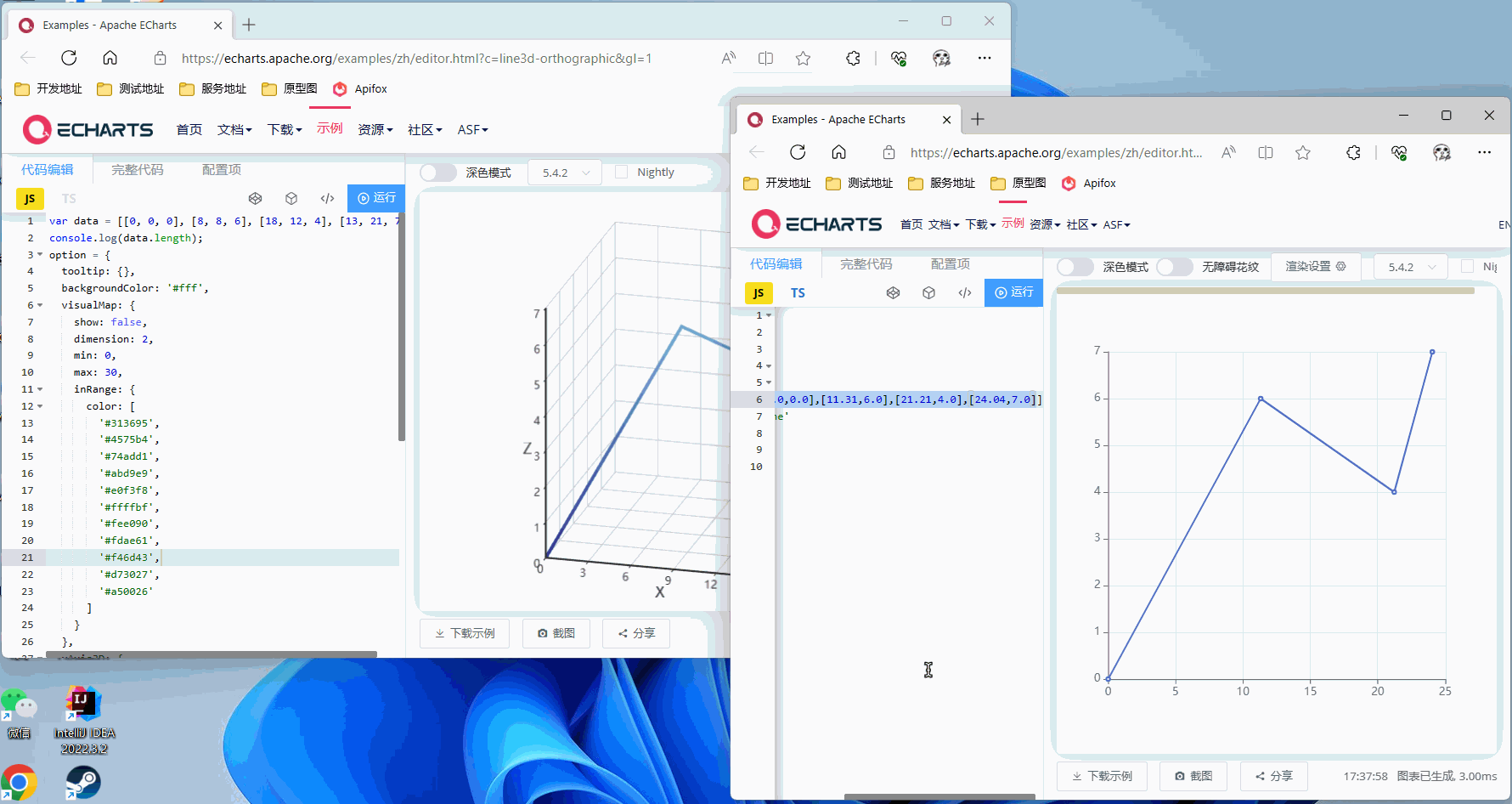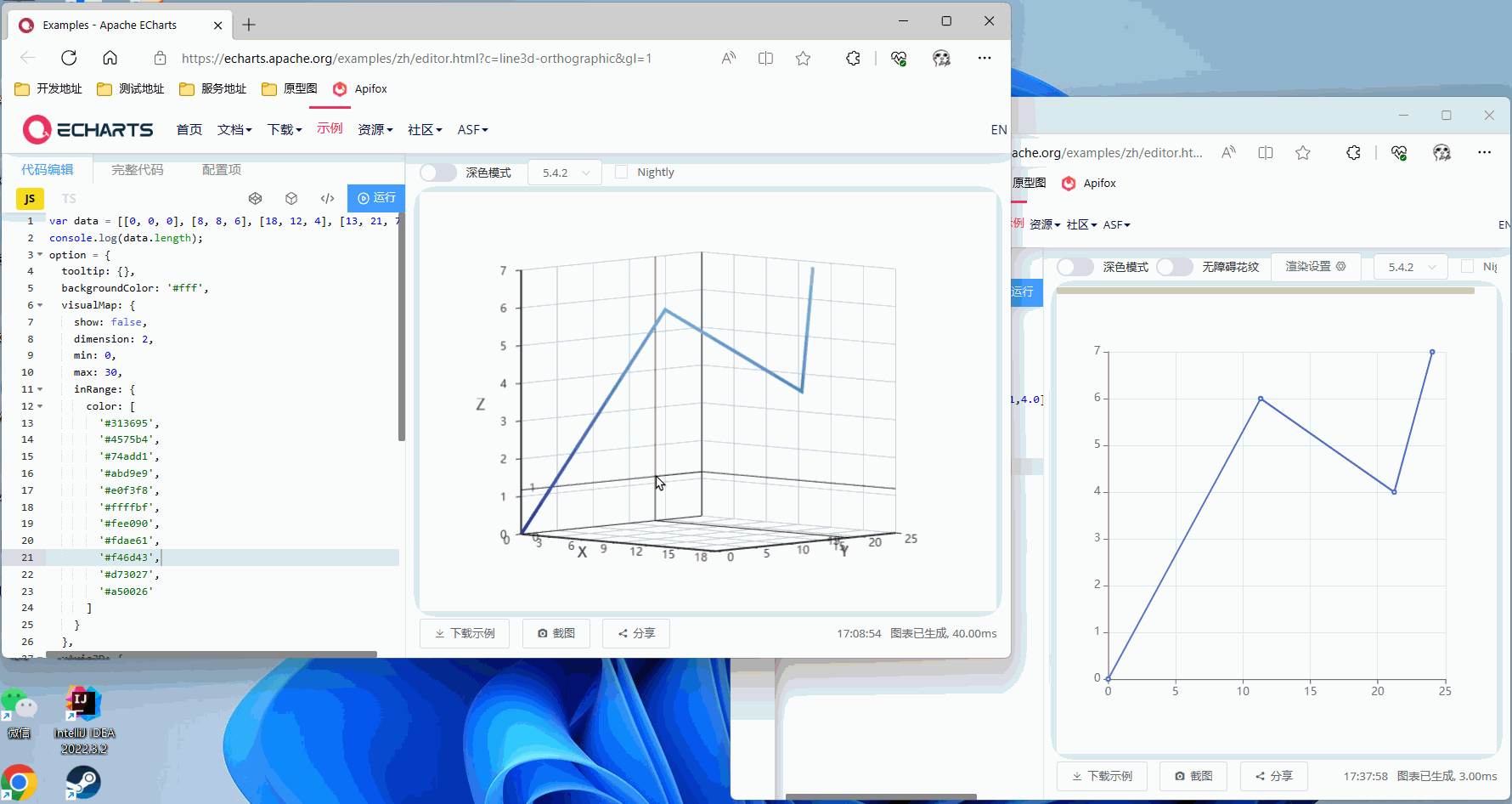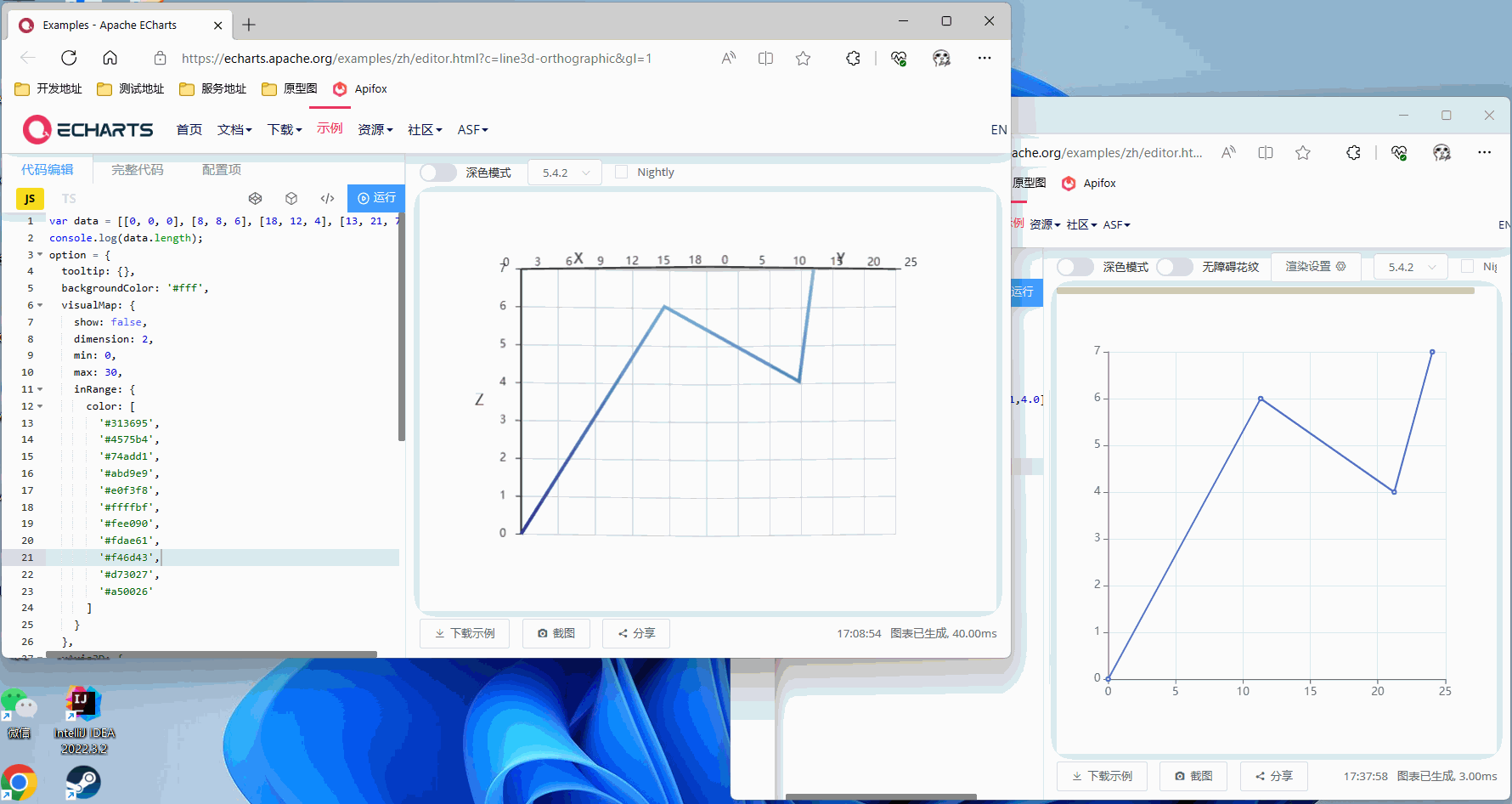
有一点比较可惜，经过测试改代码仅支持单轴旋转，如果同时旋转两个轴以上效果就会有问题，不过单轴旋转已经可以满足我项目的需求，就不再花费时间研究这个东西了，有兴趣可自行钻研joml这个框架，如果您解决了多轴旋转的问题还请回来留个言，可以帮助到更多人

代码地址：https://gitee.com/zhang_hanzhe/example-java/tree/master/springboot-proj-coord