【BZOJ4804】欧拉心算 莫比乌斯反演+线性筛

【BZOJ4804】欧拉心算

Description

给出一个数字N

Input

第一行为一个正整数T，表示数据组数。

接下来T行为询问，每行包含一个正整数N。

T<=5000,N<=10^7

Output

按读入顺序输出答案。

Sample Input

1
10

Sample Output

136

题解：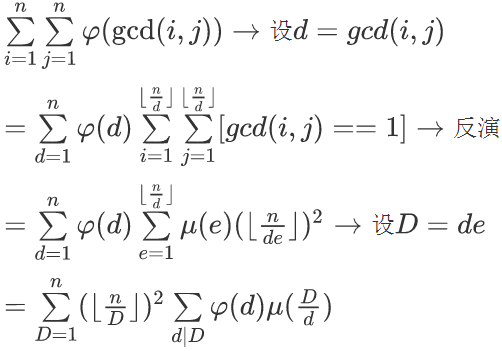

显然，$\varphi$和$\mu$都是积性函数，卷起来肯定也是积性函数，可以线性筛来搞。但是本蒟蒻到这里就卡住了，怎么线性筛啊？于是找题解，发现题解都说很简单。无奈，只好打表找规律了。（一开始表还打错了QAQ）

设$f(i)=\sum\limits_{d|i}\varphi(d)\mu({i\over d})$因为是积性函数，所以若$n=\prod p_i^{e_i}$（pi是质数），那么$f(n)=\prod f(p_i^{e_i})$，所以我们只需要找出每个质数的n次方的f值的规律。发现如下规律：

$f(p^x)=\left\{ \begin{matrix} p-2 & x=1 \\ (p-1)^2  & x=2 \\ (p-1)^2p^{x-2} & x >2\end{matrix}\right.$

然后预处理出f，分块就行了。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int m=10000000;
int n,num;
typedef long long ll;
int pri[1000010];
ll s[m+10];
bool np[m+10];
ll ans;
int main()
{
	s[1]=1;
	int i,j,last,T;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,s[i]=i-2;
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				if((i/pri[j])%pri[j]==0)	s[i*pri[j]]=s[i]*pri[j];
				else	s[i*pri[j]]=s[i/pri[j]]*(pri[j]-1)*(pri[j]-1);
				break;
			}
			s[i*pri[j]]=s[i]*(pri[j]-2);
		}
	}
	for(i=2;i<=m;i++)	s[i]+=s[i-1];
	scanf("%d",&T);
	while(T--)
	{
		ans=0;
		scanf("%d",&n);
		for(i=1;i<=n;i=last+1)
		{
			last=n/(n/i);
			ans+=(s[last]-s[i-1])*(n/i)*(n/i);
		}
		printf("%lld\n",ans);
	}
	return 0;
}