POJ1024 Tester Program

题目来源：http://poj.org/problem?id=1024

题目大意：

　　有一个迷宫，迷宫的起点在（0,0）处。给定一条路径，和该迷宫墙的设置，要求验证该路径是否为唯一的最短路径，该种墙的设置中是否存在多于的墙，可结合图进行理解。

　

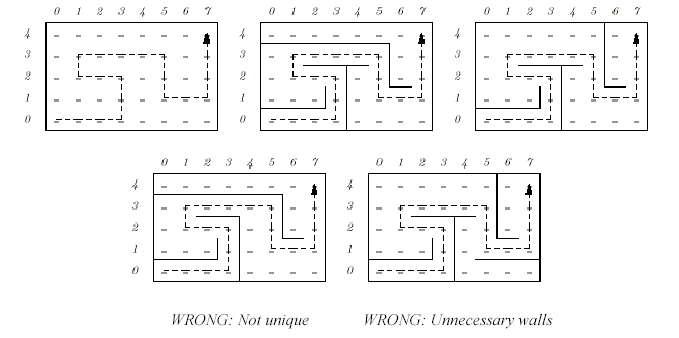
输入：第一行制定测试用例数。每个测试用例的第一行为两个正整数，指明迷宫的长和宽。接下来是给定的最短路径，用由L（左）R（右）U（上）D（下）组成的字符串表示。然后输入一个正整数m表示墙的个数。后接m行，每行四个整数，前两个整数和后两个整数分别组成两个坐标，表示该面墙把这两个点之间的路径隔断。

输出：若符合条件输出CORRECT否则输出INCORRECT。

---

Sample Input

2
8 5
RRRUULLURRRRDDRRUUU
19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
4 3
RRRUU
2
2 2 3 2
2 2 2 1

Sample Output

CORRECT
INCORRECT

---

一开始没有什么想法，看了Discuss里的讨论和一些解题报告，思路很高明。

1. bfs求各点到源点的最小步数

2. bfs求各点到终点的最小步数

3. 遍历所有网格点，如果某不在路径上的点，到源点的步数+到终点的步数<=给定的路径，则给定的路径不是唯一最短

4. 检查每堵墙，如果把墙两侧点 到起点和到终点的步长加起来+1 > 给定路径的长度,则该墙多余。（如果拆掉这堵墙，唯一最短路径不变就说明多余）

 //////////////////////////////////////////////////////////////////////////
 //        POJ1024 Tester Program
 //        Memory: 368K        Time: 16MS
 //        Language: C++        Result: Accepted
 //////////////////////////////////////////////////////////////////////////

 #include <iostream>
 #include <string>
 #include <queue>
 using namespace std;

 struct Grid {
     bool inpath;    // 是否是路径方格
     bool uwal;      // 是否有上墙
     bool rwal;      // 是否有右墙
     int scnt;       // 到源点步数
     int dcnt;       // 到终点步数
 };

 int main(void) {
     bool ok;
     int w, h, cnt, steps;   // 1 <= w, h <= 100
     string path;
     Grid grid[][];
     queue<pair<int, int> > q;

     int t, x, y, desx, desy, x2, y2, i;
     for (cin >> t; t > ; --t) {
         //初始化数据
         cin >> w >> h;
         for (y = ; y < h; ++y) {
             for (x = ; x < w; ++x) {
                 grid[y][x].inpath = false;
                 grid[y][x].uwal = false;
                 grid[y][x].rwal = false;
                 grid[y][x].scnt = -;
                 grid[y][x].dcnt = -;
             }
         }
         cin >> path;
         x = , y = ;
         grid[][].inpath = true;
         steps = path.size();
         for (i = ; i < steps; ++i) {
             switch (path[i]) {
             case 'U': ++y; break;
             case 'D': --y; break;
             case 'L': --x; break;
             case 'R': ++x; break;
             }
             grid[y][x].inpath = true;
         }
         desx = x, desy = y;
         cin >> cnt;
         for (i = ; i < cnt; ++i) {
             cin >> x >> y >> x2 >> y2;
             if (x == x2)
                 if (y +  == y2) grid[y][x].uwal = true;
                 else grid[y2][x].uwal = true;
             else
                 if (x +  == x2) grid[y][x].rwal = true;
                 else grid[y][x2].rwal = true;
         }

         //求各点到源点的最小步数（BFS）
         q.push(make_pair(, ));
         grid[][].scnt = ;
         while (!q.empty()) {
             y = q.front().first, x = q.front().second;
             if (y < h -  && grid[y][x].uwal == false && grid[y + ][x].scnt == -) {
                 grid[y + ][x].scnt = grid[y][x].scnt + ;
                 q.push(make_pair(y + , x));
             }
             if ( < y && grid[y - ][x].uwal == false && grid[y - ][x].scnt == -) {
                 grid[y - ][x].scnt = grid[y][x].scnt + ;
                 q.push(make_pair(y - , x));
             }
             if ( < x && grid[y][x - ].rwal == false && grid[y][x - ].scnt == -) {
                 grid[y][x - ].scnt = grid[y][x].scnt + ;
                 q.push(make_pair(y, x - ));
             }
             if (x < w -  && grid[y][x].rwal == false && grid[y][x + ].scnt == -) {
                 grid[y][x + ].scnt = grid[y][x].scnt + ;
                 q.push(make_pair(y, x + ));
             }
             q.pop();
         }

         //求各点到终点的最小步数（BFS）
         q.push(make_pair(desy, desx));
         grid[desy][desx].dcnt = ;
         while (!q.empty()) {
             y = q.front().first, x = q.front().second;
             if (y < h -  && grid[y][x].uwal == false && grid[y + ][x].dcnt == -) {
                 grid[y + ][x].dcnt = grid[y][x].dcnt + ;
                 q.push(make_pair(y + , x));
             }
             if ( < y && grid[y - ][x].uwal == false && grid[y - ][x].dcnt == -) {
                 grid[y - ][x].dcnt = grid[y][x].dcnt + ;
                 q.push(make_pair(y - , x));
             }
             if ( < x && grid[y][x - ].rwal == false && grid[y][x - ].dcnt == -) {
                 grid[y][x - ].dcnt = grid[y][x].dcnt + ;
                 q.push(make_pair(y, x - ));
             }
             if (x < w -  && grid[y][x].rwal == false && grid[y][x + ].dcnt == -) {
                 grid[y][x + ].dcnt = grid[y][x].dcnt + ;
                 q.push(make_pair(y, x + ));
             }
             q.pop();
         }

         //判断路径是否唯一最短，以及墙是否多余
         ok = true;
         for (y = ; y < h && ok; ++y) {
             for (x = ; x < w && ok; ++x) {
                 if (grid[y][x].scnt == - || grid[y][x].dcnt == -)
                     ok = false;     // 是否有封闭区域
                 if (y < h -  && grid[y][x].uwal
                     && grid[y][x].scnt + grid[y + ][x].dcnt +  > steps
                     && grid[y][x].dcnt + grid[y + ][x].scnt +  > steps)
                     ok = false;     // 是否上墙多余
                 if (x < w -  && grid[y][x].rwal
                     && grid[y][x].scnt + grid[y][x + ].dcnt +  > steps
                     && grid[y][x].dcnt + grid[y][x + ].scnt +  > steps)
                     ok = false;     // 是否右墙多余
                 if (!grid[y][x].inpath && grid[y][x].scnt + grid[y][x].dcnt <= steps)
                     ok = false;     // 是否存在更短路径或另一最短路径
             }
         }
         if(ok) cout << "CORRECT" << endl;
         else cout << "INCORRECT" << endl;
     }
     return ;
 }