旋转矩阵(Rotate Matrix)的性质分析

博客转载自：http://www.cnblogs.com/caster99/p/4703033.html

学过矩阵理论或者线性代数的肯定知道正交矩阵（orthogonal matrix）是一个非常好的矩阵，为什么这么说？原因有一下几点：

1. 正交矩阵每一列都是单位矩阵，并且两两正交。最简单的正交矩阵就是单位阵。
2. 正交矩阵的逆（inverse）等于正交矩阵的转置（transpose）。同时可以推论出正交矩阵的行列式的值肯定为正负1的。
3. 正交矩阵满足很多矩阵性质，比如可以相似于对角矩阵等等。

以上可以看出正交矩阵是非常特殊的矩阵，而本文题目中的旋转矩阵就是一种正交矩阵！它完美的诠释了正交矩阵的所有特点。

先说一下什么是旋转矩阵？如图1所示，我们假设最开始空间的坐标系X_A，Y_A，Z_A就是笛卡尔坐标系，这样我们得到空间A的矩阵V_A={X_A，Y_A，Z_A}^T，其实也可以看做是单位阵E。进过旋转后，空间A的三个坐标系变成了图1中红色的三个坐标系X_B，Y_B，Z_B，得到空间B的矩阵V_B={X_B，Y_B，Z_B}^T。我们将两个空间联系起来可以得到V_B=R•V_A，这里R就是我们所说的旋转矩阵。

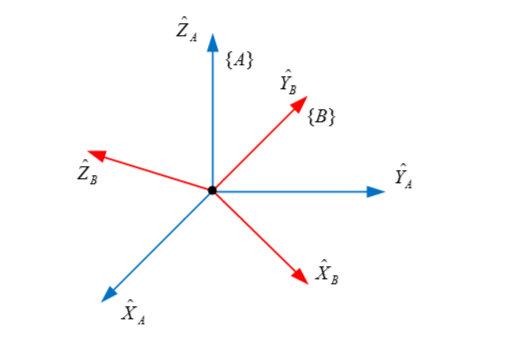
图1

由于X_A={1,0,0}^T，Y_A={0,1,0}^T，Z_A={0,0,1}^T，结合图2可以看出，旋转矩阵R就是由X_B，Y_B，Z_B 三个向量组成的。讲到这里，大家应该会发现旋转矩阵R满足第一个条件，因为单位向量无论怎么旋转长度肯定不会变而且向量之间的正交性质也不会变。那么旋转矩阵就是正交阵！不过这还不能说明问题，下面我更进一步利用数学公式进行证明。

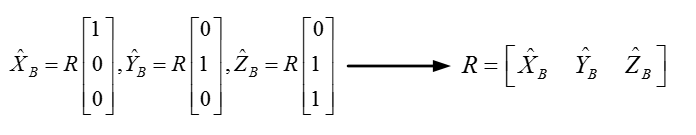
图2

进一步讨论之前，我们先说两点数学知识。（1）点乘（dot product）的几何意义：如图3，我们从点乘的公式可以得到α•β相当与β的模乘上α在β上投影的模，所以当|β|=1时，α•β就是指α在β上投影的模。这一点在下面的内容中非常重要。（2）旋转矩阵逆的几何意思：这个比较抽象，不过也好理解。旋转矩阵相当于把一个向量（空间）旋转成新的向量（空间），那么逆可以理解为由新的向量（空间）转回原来的向量（空间）。

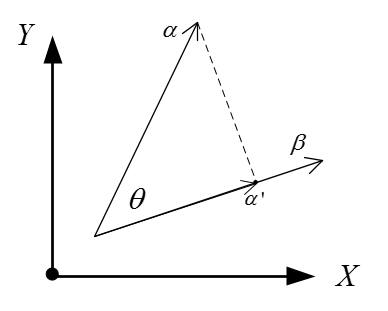
图3

接下来就是重点了，我们结合图4进行分析。上面已经说明了，旋转矩阵R就是由X_B，Y_B，Z_B 三个向量组成的。我们来看看X_B，Y_B，Z_B究竟是什么？由于图中所有的向量均是单位向量，所以X_B与X_A点乘的结果可以看成X_B在X_A上的投影的模，也就是X_B在空间A中x轴的分量！！图中中间的位置列出了X_B向量中的三个分量分别为X_B在X_A上的投影的模、X_B在Y_A上的投影的模和X_B在Z_A上的投影的模。这从几何角度很好理解。以此类推，可以得出的旋转矩阵R的表达形式。我们根据图4可以惊喜的发现，矩阵R的第一行就是X_A在X_B，Y_B，Z_B上的投影的模，也就是X_A^T。

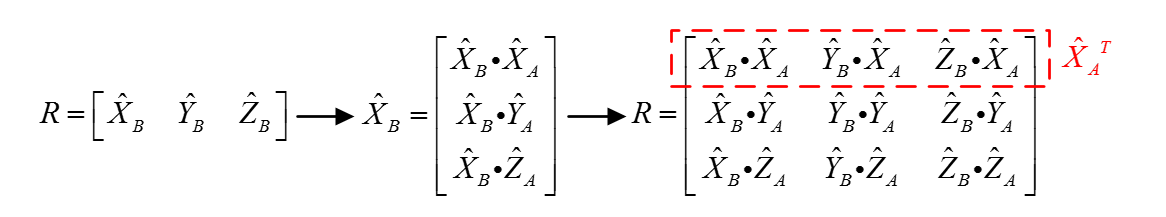
图4

这个发现有什么用呢？图5做出解释。根据上面公式可以推出A到B的旋转矩阵等于B到A的旋转矩阵的转置。根据我们上一段所说的A到B的旋转矩阵的逆就是等于B到A的旋转矩阵，因此很容易推出R^_-1等于R^T！这满足正交矩阵的第二个条件，又一次证明了旋转矩阵就是正交阵。在平时的工作中，我也测试过所有的旋转矩阵的行列式的值都是为1的，所以旋转矩阵满足正交阵的一切性质，可以说是很完美的矩阵。

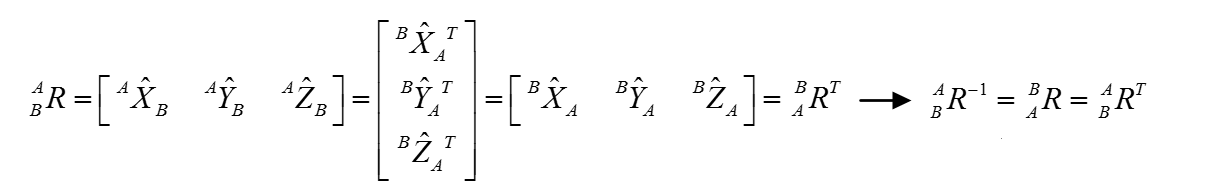
图5

现在以三个欧拉角中的RotX为例（其余两个欧拉角以此类推），验证一下以上说的结论。

　　首先结合图5的公式，计算出RotX的旋转矩阵R_rotx。

• 由于X轴是垂直于YoZ平面的，所以X_A和Y_B，Z_B的点乘结果为0，同时X_B和Y_A，Z_A的点乘结果也为0。
• 由于X_A，X_B都是单位向量，所以X_A和X_B的点乘结果为1。
• 由于绕x轴旋转，所以我们观察Y_B和Z_B分别在Y_A和Z_A上的投影情况，如图6，我已经将坐标标注了。
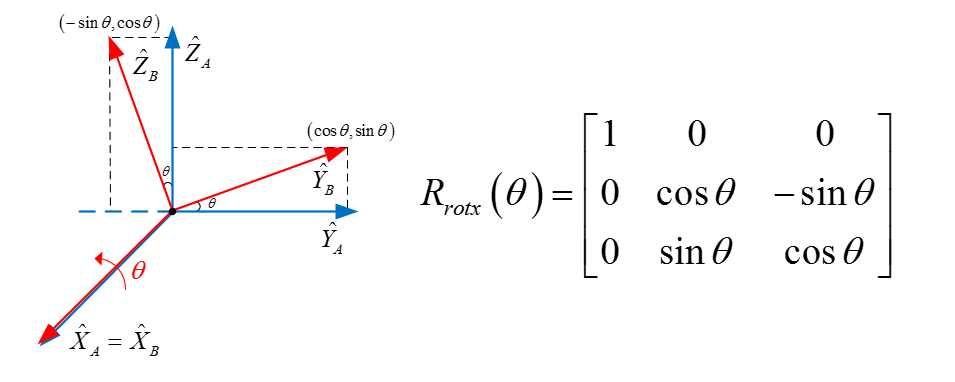
• 图6
• 这样就完成旋转矩阵R_rotx，我们接下来验证一下。
• 1. 我们计算每一行每一列的模，都为1；并且任意两个列向量或者任意两个行向量都是正交的。所以满足上文列出的第一个性质。
  2. 我们计算R_rotx的行列式，很简单可以算出为1。这时我们计算一下该矩阵的逆和转置，这里我不写出来了是相等的。所以满足上文列出的第三个性质。
  3. 第三个性质要牵扯到更多的数学知识，在这里就不验证了。

  　　总结一下：旋转矩阵是一个完美的矩阵——正交矩阵。它的行列式为1，且每个列向量都是单位向量且相互正交，它的逆等于它的转置。