Lasso估计论文学习笔记(一)
最近课程作业让阅读了 这篇经典的论文,写篇学习笔记。
这篇经典的论文,写篇学习笔记。
主要是对论文前半部分Lasso思想的理解,后面实验以及参数估计部分没有怎么写,中间有错误希望能提醒一下,新手原谅一下。
1.整体思路
作者提出了一种收缩和选择方法Lasso,这是一种可以用于线性回归的新的估计方法。它具有子集选择和岭回归的各自的优点。像子集选择一样可以给出具有解释力的模型,又能像岭回归一样具有可导的特性,比较稳定。同时避免了子集选择不可导,部分变化引起整体巨大变化这一不稳定的缺点。以及岭回归不能很好的收缩到0的缺点。
2.对文章目的理解
为了理解这篇文章是做了什么事情,先要明白回归的收缩和选择是用来做什么的。
我们用某一个模型F来回归拟合某一问题时,往往容易遇到过拟合的问题。这是经常是由于,模型过于复杂,比如参数过多,变量指数过高。过度拟合了训练数据,导致模型的泛化能力变差。这是需要引入正则化项(惩罚项)来使模型最后训练的结果不至于太过于复杂(过拟合)。
正则化一般具有如下形式:
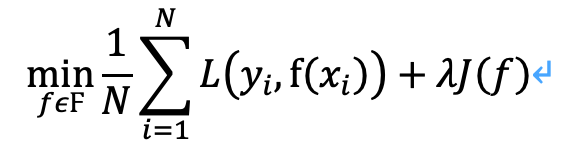
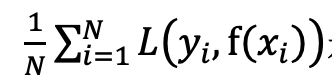 是经验风险。J(f)是正则化项,就代表了对模型复杂度的惩罚,只要它能做到模型越复杂,J(f)值越大。所以最小化损失函数时,就会令经验风险尽量小的同时,考虑让模型复杂度也不要太大。这样虽然会提高模型的训练误差,甚至可能某些正则化操作会使模型偏差(Bias)变大,但是会提高模型的稳定程度(方差更小,模型更简单),减少模型的泛化误差。
是经验风险。J(f)是正则化项,就代表了对模型复杂度的惩罚,只要它能做到模型越复杂,J(f)值越大。所以最小化损失函数时,就会令经验风险尽量小的同时,考虑让模型复杂度也不要太大。这样虽然会提高模型的训练误差,甚至可能某些正则化操作会使模型偏差(Bias)变大,但是会提高模型的稳定程度(方差更小,模型更简单),减少模型的泛化误差。
这里有两个问题!
(1) 模型的简单体现在什么方面?(模型如何简化)
(2) 正则化是怎么让模型变简单的?
先说问题(1),考虑模型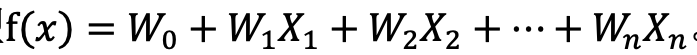 。向量X是特征向量,向量W是其对应的参数。模型复杂,一是体现在特征过多,第二是体现在X的指数过高。那么如何令模型变得简单呢,自然而然的想到若某些参数为0,那么就相当于不考虑这些特征Xi了(这就是子集选择的思想)。或者令某些参数缩小,这样不重要的特征对结果造成的影响也会变小(这就是shrinkage的思想)。当然有些参数在缩小过程中会变成0,这就是在收缩过程中起到了子集选择的效果。
。向量X是特征向量,向量W是其对应的参数。模型复杂,一是体现在特征过多,第二是体现在X的指数过高。那么如何令模型变得简单呢,自然而然的想到若某些参数为0,那么就相当于不考虑这些特征Xi了(这就是子集选择的思想)。或者令某些参数缩小,这样不重要的特征对结果造成的影响也会变小(这就是shrinkage的思想)。当然有些参数在缩小过程中会变成0,这就是在收缩过程中起到了子集选择的效果。
那么关键的来了,问题(2)正则化是怎么让模型变简单的呢。上一段分析出,如果让某些不重要的参数进行收缩,能够使模型变得简化。再来看看正则化的例子:
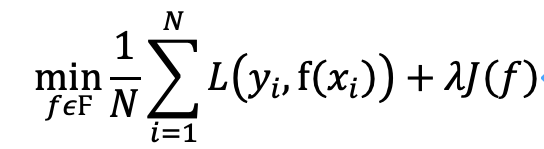
以J(f)取||w||为例,可以看出,如果参数W越多,或者整理模的平方和越大,||w||就越大。所以在最小化代价函数的过程,就会考虑让参数的平方和也尽可能小(整体最小的前提下)。所以设不加正则化项的估计出的向量为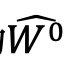 ,加了正则化项的估计出得参数向量为
,加了正则化项的估计出得参数向量为 。那么可以看出
。那么可以看出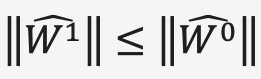 。所以正则化项起到了shrinkage参数的效果,如果有些参数在收缩过程中精确到0,就相当于子集选择的效果(我们是希望这样的)。
。所以正则化项起到了shrinkage参数的效果,如果有些参数在收缩过程中精确到0,就相当于子集选择的效果(我们是希望这样的)。
那么这篇文章的目的就可以理解了,作者提出的Lasso就是一种具有岭回归(可导可直接求最小值)和子集选择(部分参数为0)的优点的估计方法(也可以说一种正则化的方法)。
3.方法对比及Lasso引入
之前是在word写的,这里为了方便截图一下。

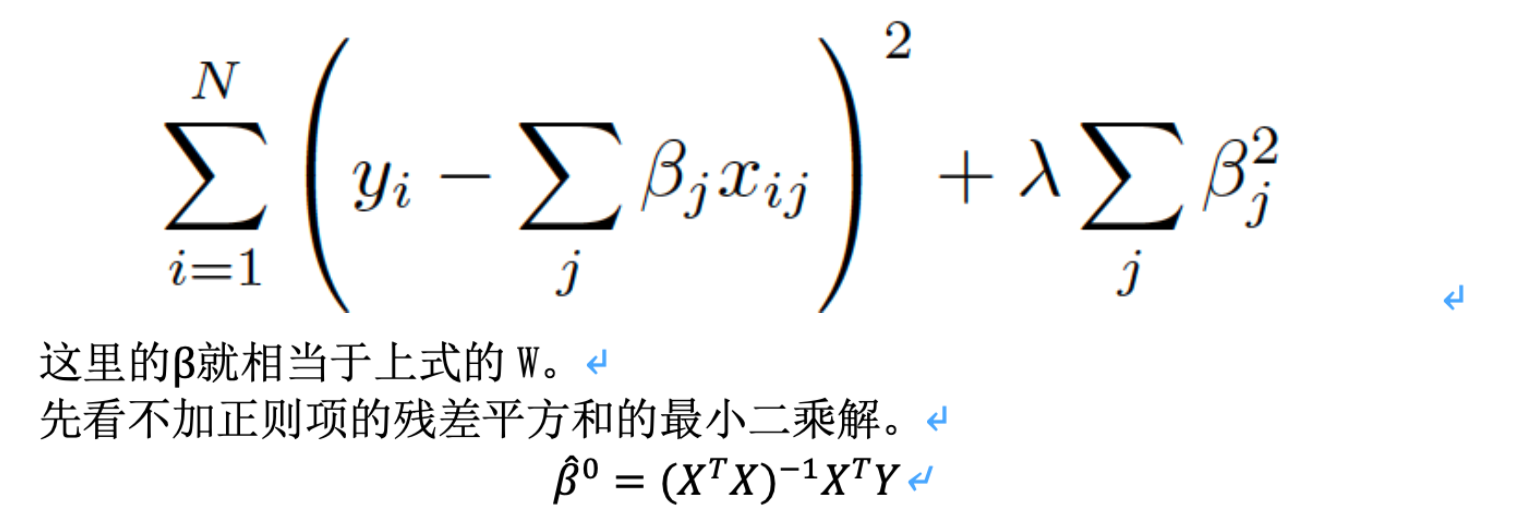
Lasso估计论文学习笔记(一)的更多相关文章
- 论文学习笔记 - 高光谱 和 LiDAR 融合分类合集
A³CLNN: Spatial, Spectral and Multiscale Attention ConvLSTM Neural Network for Multisource Remote Se ...
- Apache Calcite 论文学习笔记
特别声明:本文来源于掘金,"预留"发表的[Apache Calcite 论文学习笔记](https://juejin.im/post/5d2ed6a96fb9a07eea32a6f ...
- Raft论文学习笔记
先附上论文链接 https://pdos.csail.mit.edu/6.824/papers/raft-extended.pdf 最近在自学MIT的6.824分布式课程,找到两个比较好的githu ...
- 论文学习笔记--无缺陷样本产品表面缺陷检测 A Surface Defect Detection Method Based on Positive Samples
文章下载地址:A Surface Defect Detection Method Based on Positive Samples 第一部分 论文中文翻译 摘要:基于机器视觉的表面缺陷检测和分类可 ...
- 论文学习笔记 - Classifification of Hyperspectral and LiDAR Data Using Coupled CNNs
Classifification of Hyperspectral and LiDAR Data Using Coupled CNNs 来源:IEEE TGRS 2020 下载:https://arx ...
- QA问答系统,QA匹配论文学习笔记
论文题目: WIKIQA: A Challenge Dataset for Open-Domain Question Answering 论文代码运行: 首先按照readme中的提示安装需要的部分 遇 ...
- Lasso估计学习笔记(二)
先看Lasso估计学习笔记(一),这篇是续的上一篇
- 深度学习笔记(七)SSD 论文阅读笔记简化
一. 算法概述 本文提出的SSD算法是一种直接预测目标类别和bounding box的多目标检测算法.与faster rcnn相比,该算法没有生成 proposal 的过程,这就极大提高了检测速度.针 ...
- 深度学习笔记(七)SSD 论文阅读笔记
一. 算法概述 本文提出的SSD算法是一种直接预测目标类别和bounding box的多目标检测算法.与faster rcnn相比,该算法没有生成 proposal 的过程,这就极大提高了检测速度.针 ...
随机推荐
- 数据结构-堆栈和队列最简单的实现(Python实现)
OK,上篇博客我们介绍了双向链表以及代码实现,这篇文章我们来学习堆栈和队列. 队.栈和链表一样,在数据结构中非常基础一种数据结构,同样他们也有各种各样.五花八门的变形和实现方式.但不管他们形式上怎么变 ...
- infiniband install driver
硬件:Mellanox InfiniBand,主要包括 HCA(主机通道适配器)和交换机两部分 软件:CentOS 6.4 MLNX_OFED_LINUX-2.1-1.0.0-rhel6.4-x86_ ...
- 个人永久性免费-Excel催化剂功能第31波-数量金额分组凑数功能,财务表哥表姐最爱
在财务工作过程中,很大时候需要使用到凑数的需求,花了两三天时间认真研究了一下,本人水平也只能做代码搬运工,在用户体验上作了一下完善.完成了Excel版的凑数功能. 文章出处说明 原文在简书上发表,再同 ...
- Spark学习之第一个程序 WordCount
WordCount程序 求下列文件中使用空格分割之后,单词出现的个数 input.txt java scala python hello world java pyfysf upuptop wintp ...
- [剑指offer] 40. 数组中只出现一次的数字
题目描述 一个整型数组里除了两个数字之外,其他的数字都出现了偶数次.请写程序找出这两个只出现一次的数字. 思路: 解法一: 哈希表 class Solution { public: void Find ...
- spring applicationContext.xml文件移到resources目录下
SpringMVC的框架默认目录结构 修改后的目录结构及web.xml 同时在pom里的配置:将resources目录打包到web-inf/classes目录下<resources> ...
- Git学习(二):Git的初步使用
一.Git的最小配置 1.使用如下命令创建Git的用户名和邮箱,如下所示: $git config --global user.name 'your_name' $git config --globa ...
- Web访问原理-从输入URL到页面加载完成的过程中都发生了什么事情?
从输入URL到页面加载完成的过程中都发生了什么事情?--这是一个经典的面试题: 主要是关于计算机网络方面的知识基础,对于非科班计算机自学web开发的同学可能理解起来就很困难. StackOverFlo ...
- S2第四章
- 从深处去掌握数据校验@Valid的作用(级联校验)
每篇一句 NBA里有两大笑话:一是科比没天赋,二是詹姆斯没技术 相关阅读 [小家Java]深入了解数据校验:Java Bean Validation 2.0(JSR303.JSR349.JSR380) ...
