树、图、堆、STL(来自菜鸡的"炒鸡"干粮)

树、图、堆、STL

图论基础

简单图：

没有自环，两个顶点之间最多只有一条边。

完全图：

一个简单图，每两个顶点之间都有一条边。一共有(n-1)*n/2条边。

二分图：

一个简单图，设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

一般二分图都能化成：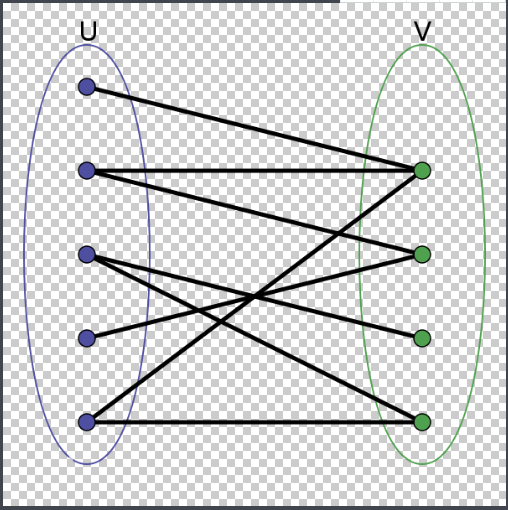

图的定义：

相邻、度数…………

有向图：

边都是单向的。

带权图：

可以给边加权，成为带权图。

稀疏图：

边与V*(V-1)相比非常少的图。他的补图为稠密图。

简单路径：

不出现重复的点。

连通图：

每两点之间都有路径。

树：

N个点，N-1条边

关于树的具体知识：

1.纳尼？？Vector(顺序表结构 向量)和List(单链表)居然不够用？？

	vector	list
search	log n	线性
insert	线性	O(1)

无法同时兼顾高效性！！

2.中间概念

边、节点、指定根、有根树、子树、孩子、父亲、度数、兄弟、祖先、后代、叶子节点。没有意外的话，上文有讲。

任何一棵树中，所含的边数应该恰好等于所有顶点度数之和，也等于顶点总数-1.

3.有序树：将同一节点的所有孩子编号使他们具有这种意义上的某一个次序

4.WTF？？原来树这么神奇？？ 树：无环连通图 极小连通图 极大无环图

5.树的半线 性 v的祖先/后代若存在，则必然/未必唯一.

6.生成树：原图的子图，是一棵树。

图/树 ( 反正是通用的 ) 的表示方法 ： 邻接矩阵与邻接表。

邻接矩阵：

优点：查找/删除一个点时间复杂度O(1)

邻接表：

优点：快速遍历某点所有数据 以及 占用空间小

缺点：查找、删除边不是常数时间。

二叉树

定义:二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

由二叉树定义以及图示分析得出二叉树有以下特点：

1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。

2）左子树和右子树是有顺序的，次序不能任意颠倒。

3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。 这点与普通的树不同。

1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）

2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）

3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。

4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。

5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;

(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；

(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

所以，二叉树的表示比普通的树的表示方便多了！！ 只需开一个数组，记录当前节点(x)以及节点编号(y)。他爸的编号就是y/2。

STL 数据结构

标准数据库，简称STL;

数据结构：

1.栈(stack)

1.1 栈的定义

栈是一种特殊的线性表。其特殊性在于限定插入和删除数据元素的操作只能在线性表的一端进行。所以，我们一般画一个桶来模拟栈的运行。

我们来实现栈：

#include <stack>
stack <int> a;
a.push(x);
a.pop();
a.empty();
a.top();

2.队列(queue)

与栈相反，队列的规则是先进后出。

#include <queue>
queue <int> a;
empty()函数返回真(true)如果队列为空，否则返回假(false)。

front()返回队列第一个元素的引用。

pop()函数删除队列的一个元素

push() 在末尾加入一个元素

size() 返回队列中元素的个数

优先队列

它是个队列，你把数据存进去，C++的STL自动帮帮你排序（你可以这么理解吧）。

#include <queue>
queue <int> a;
empty()函数返回真(true)如果队列为空，否则返回假(false)。

top()返回队列第一个元素的引用。

pop()函数删除队列的一个元素

push() 在末尾加入一个元素

size() 返回队列中元素的个数

操作与上面类似。

本文有部分参考：作者：MrHorse1992链接：https://www.jianshu.com/p/bf73c8d50dc2来源：简书简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。