3D数学基础（三）矩阵

　　3D引擎中对于矩阵的使用非常多，介绍这些知识也是为了告诉开发者原理，更有助于开发者编写逻辑。

　　（1）固定流水线

　　各种坐标系之间的转化是通过矩阵相乘得到的，这里面就涉及到了3D固定流水线。作为3D游戏开发者，必须要知道两个流水线：一个是固定流水线，一个是可编程流水线。

　　固定流水线主要原理是3D模型在屏幕上显示是按照一定得固定流程来完成的，这个固定的流程就是固定流水线。鸡蛋来说就是一个3D物体在显示器上成像的过程。

　　局部坐标-->世界坐标-->观察坐标-->消隐-->光照-->透视坐标-->视口坐标-->光栅化

　　物体从最初的局部坐标经过一系列的矩阵变换转换到另一个坐标系，转换矩阵中最重要的就是模型（Model）矩阵、视图（View）矩阵、投影（Projection）矩阵。首先，顶点坐标开始与局部空间，也就是局部坐标（Local Coordinate），经过世界坐标（World Coordinate），观察坐标（View Coordinate），裁剪坐标（Clip Coordinate），最后以屏幕坐标（Screen Coordinate）结束，最终目的是将物体在屏幕上展现出来。

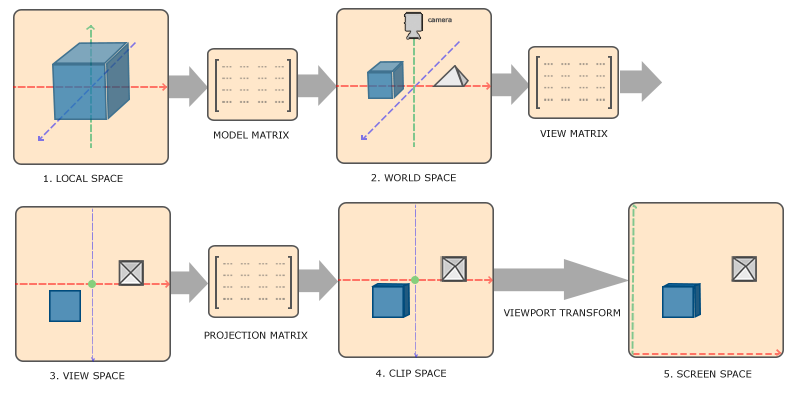
　　便于理解，总结归纳一下：

　　1.局部坐标是对相对于局部原点的坐标，也是对象开始的坐标。

　　2.将局部坐标转换为世界坐标，世界坐标是作为一个更大空间范围的坐标系。这些坐标是相对于世界原点的。

　　3.将世界坐标转换为观察坐标，观察坐标是指以摄像机或者观察者的角度观察的坐标。

　　4.在将坐标处理到观察坐标之后，我们需要将其投影到裁剪坐标上。裁剪坐标是在-1.0到1.0范围内判断哪些顶点会出现在屏幕上的。

　　5.最后将裁剪坐标转换为屏幕坐标，这一过程称为视口变换（ViewportTransform）。视口变换将位于-1.0到1.0范围内的坐标转换到视口函数所定义的坐标范围内。转换的坐标将会送到光栅器中，由光栅器转换为片段。

　　总体来说，就是3D建模工具导出的模型是要将起模型位置重置为（0，0，0）,j将其拖放到Unity编辑器里面。在默认情况下，与世界系坐标为重合在（0，0，0）位置上。然而物体不能都堆放在世界中心点，在将其拖动到其他位置上来的这一过程就是引擎内部实现了把模型从局部坐标到世界坐标的变换，即和世界矩阵相乘得到的。接着要从程序中看到这个场景，就需要放置一个虚拟摄像机，将物体放到虚拟摄像机里面就是把物体从世界坐标转换到观察坐标，即与摄像机矩阵相乘得到的，当然后面要做消隐，就是背面消除，因为只能看到物体的正面，为了优化效率考虑背面不需要绘制出来。打上灯光让场景明亮起来，就可以通过虚拟摄像机来观察虚拟世界了。因为虚拟摄像机和人眼一样有观察距离，眼睛两侧的物体是看不到的，而看不到的物体就可以将其裁剪掉，这一过程涉及到了观察坐标到透视坐标的转换，为了方便计算将物体做投影计算。为了显示屏幕上看到，将其转化到视口坐标上。最后就是光栅化了。这样固定流水线就完成了。

　　（2）可编程流水线

　　硬件的发展使得显卡的运算能力得到了很大提升，也就是通常说的GPU编程。在显卡不发达是，绘制3D物体都是通过固定流水线实现的，随着显卡的提高，就有了可编程流水线。可编程流水线其实就是把CPU上进行运算搬到显卡的GPU中运算。也就是说矩阵之间的还算放到GPU中计算，可以把CPU解放出来。

　　（3）平移矩阵

　　在3D空间中，把一个对象从一个位置移到另一个位置，在引擎底层进行了平移矩阵换算。在3D空间中，把对象从P点移动到P‘点，运用数学公式可以计算出而二者的转化关系。

　　x'=x+T_x；y'=y+T_y；z'=z+T_z

　　根据这些多项式可以将它们换算成一个通用的并且可以使用矩阵表示的公式。

　　

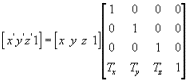
　　需要注意一点的是在进行矩阵计算的时候，需要将三维的点转化为齐次坐标，进行3D计算，如果不转换，矩阵的线性变换是很难实现的，比如物体的平移变换、缩放变换等三维矩阵是无法完成的。

　　向量和点都是三维的，如果使用的是点，就在点的最后再加一项1，齐次坐标就表示为（x,y,z,1）。如果是用的是向量，就在向量的最后加一项0，齐次坐标就表示为（x,y,z,0）。但是向量不可以通过矩阵换算的，点可以。在Unity中只需要拖拉就可以变换位置。

　　（4）缩放矩阵

　　在3D空间中对于物体的缩放并不是凭空产生的，也是经过运算得到的。运算公式为:

　　x'=x*S_x；y'=y*S_y；z'=z*S_z

　　上述公式可以写成矩阵换算，如下所示。

　　

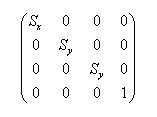
　　在Unity编辑器的实际操作中，引擎内部就实现了矩阵的放缩，只需简单操作即可。

　　（5）矩阵旋转

　　在3D游戏开发中,游戏中的3D物体旋转可以通过矩阵旋转，四元数旋转，欧拉角旋转得到。矩阵旋转最基本的是绕X、Y、Z轴旋转。矩阵玄真在引擎中使用的比较多，编程时一般采用四元数或者是欧拉角实现。下面说的是绕X、Y、Z轴的旋转矩阵。

　　绕X轴旋转的矩阵

　　

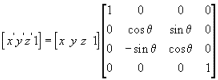
　　绕Y轴旋转的矩阵

　　

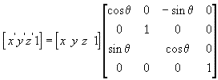
　　绕Z轴旋转的矩阵

　　

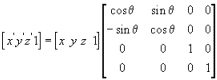
　　这些时矩阵在3D游戏中的计算方式，Unity引擎已经为开发者提供了旋转接口，函数transform.Rotate（new Vector3(0,1,0)）表示绕Y轴旋转，在Rotate函数中使用了向量，它们的参数表示为x,y,z，在上述算式中y的值为1表示绕Y周迅段传，依此类推。