自相关系数 ACF与偏自相关系数PACF,拖尾和截尾
1、ACF
y(t,s)=E(Xt-µt)(Xs-µs)
定义ρ(t,s)为时间序列的自相关系数,为ACF
ρ(t,s)=y(t,s)/sqrt(DXt * DXs)
E为期望,D为方差
2、PACF
自相关系数ρ(t,s)并不是只有两个点t和s的数据决定的。而是还包含了t-1 ~ s+1时间段值的影响。而PACF是严格这两个变量之间的相关性。
3、拖尾与截尾
拖尾是指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小
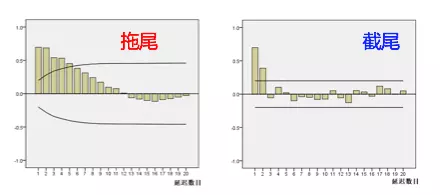
出现以下情况,通常视为(偏)自相关系数d阶截尾:
- 在最初的d阶明显大于2倍标准差范围
- 之后几乎95%的(偏)自相关系数都落在2倍标准差范围以内
- 且由非零自相关系数衰减为在零附近小值波动的过程非常突然

出现以下情况,通常视为(偏)自相关系数拖尾:
1)如果有超过5%的样本(偏)自相关系数都落入2倍标准差范围之外
2)或者是由显著非0的(偏)自相关系数衰减为小值波动的过程比较缓慢或非常连续
自相关系数 ACF与偏自相关系数PACF,拖尾和截尾的更多相关文章
- 数理统计7:矩法估计(MM)、极大似然估计(MLE),定时截尾实验
在上一篇文章的最后,我们指出,参数估计是不可能穷尽讨论的,要想对各种各样的参数作出估计,就需要一定的参数估计方法.今天我们将讨论常用的点估计方法:矩估计.极大似然估计,它们各有优劣,但都很重要.由于本 ...
- ARIMA模型总结
时间序列建模基本步骤 获取被观测系统时间序列数据: 对数据绘图,观测是否为平稳时间序列:对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列: 经过第二步处理,已经得到平稳时间序列.要对平稳时间序 ...
- ARIMA模型——本质上是error和t-?时刻数据差分的线性模型!!!如果数据序列是非平稳的,并存在一定的增长或下降趋势,则需要对数据进行差分处理!ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数
https://www.cnblogs.com/bradleon/p/6827109.html 文章里写得非常好,需详细看.尤其是arima的举例! 可以看到:ARIMA本质上是error和t-?时刻 ...
- R时间序列分析实例
一.作业要求 自选时间序列完成时间序列的建模过程,要求序列的长度>=100. 报告要求以下几部分内容: 数据的描述:数据来源.期间.数据的定义.数据长度. 作时间序列图并进行简单评价. 进行时间 ...
- 时间序列预测之--ARIMA模型
什么是 ARIMA模型 ARIMA模型的全称叫做自回归移动平均模型,全称是(ARIMA, Autoregressive Integrated Moving Average Model).也记作ARIM ...
- python时序数据分析--以示例说明
Python时间序列数据分析--以示例说明 标签(空格分隔): 时间序列数据分析 本文的内容主要来源于博客:本人做了适当的注释和补充. https://www.analyticsvidhya.com/ ...
- [python] 时间序列分析之ARIMA
1 时间序列与时间序列分析 在生产和科学研究中,对某一个或者一组变量 进行观察测量,将在一系列时刻 所得到的离散数字组成的序列集合,称之为时间序列. 时间序列分析是根据系统观察得到的时间序列数据, ...
- 基于R语言的时间序列分析预测
数据来源: R语言自带 Nile 数据集(尼罗河流量) 分析工具:R-3.5.0 & Rstudio-1.1.453 #清理环境,加载包 rm(list=ls()) library(forec ...
- 时间序列算法理论及python实现(1-算法理论部分)
如果你在寻找时间序列是什么?如何实现时间序列?那么请看这篇博客,将以通俗易懂的语言,全面的阐述时间序列及其python实现. 就餐饮企业而言,经常会碰到如下问题. 由于餐饮行业是胜场和销售同时进行的, ...
随机推荐
- 使用 Flask-Cache 缓存给Flask提速
https://blog.csdn.net/u013205877/article/details/78013289
- [OIDC in Action] 3. 基于OIDC(OpenID Connect)的SSO(添加Github OAuth 2.0的支持)
在上上一篇基于OIDC的SSO的登录页面的截图中有出现QQ登录的地方.这个其实是通过扩展OIDC的OpenID Provider来实现的,OpenID Provider简称OP,OP是OIDC的一个很 ...
- VMware Workstation 14安装VMware Tools
1 单击虚拟机,选择安装VMware Tools 2 此时会在桌面出现VWware Tools 3 双击进入 4 把*.tar.gz压缩文件cp到/home下 5 sudo tar -zvxf *. ...
- codeforces 792A-D
先刷前四题,剩下的有空补. 792A New Bus Route 题意:给出x 轴上的n 个点,问两个点之间的最短距离是多少,有多少个最短距离. 思路:排序后遍历. 代码: #include<s ...
- 一、Log4Net配置
Core的配置 一.创建core包含控制和视图的项目以及Log4Net引用 二.创建Log4Net配置文件 右击项目->添加文件 Log4Net.config 2 复制以下代码 以下配置可做 ...
- WIN10解决:失败 – 检测到病毒文件下载失败问题
欢迎访问我的个人博客四个空格,本文永久链接移至:WIN10解决:失败 – 检测到病毒文件下载失败问题 这个是Windows防火墙的原因,直接按WINDOWS键,输入windows,窗口搜索:Windo ...
- 范性for语义以及pair和ipair的区别
详情参考 lua手册 1. 范性for语义 在了解pair和ipair前先简单了解下lua中的for循环,这里只阐述范性for循环的语义,范性 for 在自己内部保存迭代函数,实际上它保存三个值:迭代 ...
- hdu P3374 String Problem
今天又在lyk大佬的博客学会了——最小表示法(异常激动发篇题解纪念一下说在前面:给luogu提个建议最小表示法的题太少了,都被hdu抢去了!!! 我们先看一下题目 看完后可以用一个字概括——蒙,两个字 ...
- [LOJ3084][GXOI/GZOI2019]宝牌一大堆——DP
题目链接: [GXOI/GZOI2019]宝牌一大堆 求最大值容易想到$DP$,但如果将$7$种和牌都考虑进来的话,$DP$状态不好设,我们将比较特殊的七小对和国士无双单独求,其他的进行$DP$. 观 ...
- subprocess
在没有subprocess这个模块的时候,我们怎么去跟我们的操作系统做交互的呐?下面我们先说说这三个模块:os.system().os.popen().commands. 1. os.system( ...
