AVL树之 Java的实现

AVL树的介绍

AVL树是高度平衡的而二叉树。它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。

上面的两张图片，左边的是AVL树，它的任何节点的两个子树的高度差别都<=1；而右边的不是AVL树，因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3，而以8为根节点的树的高度是1)。

AVL树的Java实现

1. 节点

1.1 节点定义

public class AVLTree<T extends Comparable<T>> {
    private AVLTreeNode<T> mRoot;    // 根结点

    // AVL树的节点(内部类)
    class AVLTreeNode<T extends Comparable<T>> {
        T key;                // 关键字(键值)
        int height;         // 高度
        AVLTreeNode<T> left;    // 左孩子
        AVLTreeNode<T> right;    // 右孩子

        public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
            this.key = key;
            this.left = left;
            this.right = right;
            this.height = 0;
        }
    }

    ......
}

AVLTree是AVL树对应的类，而AVLTreeNode是AVL树节点，它是AVLTree的内部类。AVLTree包含了AVL树的根节点，AVL树的基本操作也定义在AVL树中。AVLTreeNode包括的几个组成对象:
(01) key -- 是关键字，是用来对AVL树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
(04) height -- 是高度。

1.2 树的高度

/*
 * 获取树的高度
 */
private int height(AVLTreeNode<T> tree) {
    if (tree != null)
        return tree.height;

    return 0;
}

public int height() {
    return height(mRoot);
}

关于高度，有的地方将"空二叉树的高度是-1"，而本文采用维基百科上的定义：树的高度为最大层次。即空的二叉树的高度是0，非空树的高度等于它的最大层次(根的层次为1，根的子节点为第2层，依次类推)。

1.3 比较大小

/*
 * 比较两个值的大小
 */
private int max(int a, int b) {
    return a>b ? a : b;
}

2. 旋转

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

上图中的4棵树都是"失去平衡的AVL树"，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL树，如下图：

上面的两张图都是为了便于理解，而列举的关于"失去平衡的AVL树"的例子。总的来说，AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一，它们都由各自的定义：

(1) LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(2) LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(3) RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

(4) RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面RR情况中，由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍"LL(左左)，LR(左右)，RR(右右)和RL(右左)"这4种情况对应的旋转方法。

2.1 LL的旋转

LL失去平衡的情况，可以通过一次旋转让AVL树恢复平衡。如下图：

图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了AVL树，而且该旋转只需要一次即可完成。
对于LL旋转，你可以这样理解为：LL旋转是围绕"失去平衡的AVL根节点"进行的，也就是节点k2；而且由于是LL情况，即左左情况，就用手抓着"左孩子，即k1"使劲摇。将k1变成根节点，k2变成k1的右子树，"k1的右子树"变成"k2的左子树"。

LL的旋转代码

/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
    AVLTreeNode<T> k1;

    k1 = k2.left;
    k2.left = k1.right;
    k1.right = k2;

    k2.height = max( height(k2.left), height(k2.right)) + 1;
    k1.height = max( height(k1.left), k2.height) + 1;

    return k1;
}

2.2 RR的旋转

理解了LL之后，RR就相当容易理解了。RR是与LL对称的情况！RR恢复平衡的旋转方法如下：

图中左边是旋转之前的树，右边是旋转之后的树。RR旋转也只需要一次即可完成。

RR的旋转代码

/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
    AVLTreeNode<T> k2;

    k2 = k1.right;
    k1.right = k2.left;
    k2.left = k1;

    k1.height = max( height(k1.left), height(k1.right)) + 1;
    k2.height = max( height(k2.right), k1.height) + 1;

    return k2;
}

2.3 LR的旋转

LR失去平衡的情况，需要经过两次旋转才能让AVL树恢复平衡。如下图：

第一次旋转是围绕"k1"进行的"RR旋转"，第二次是围绕"k3"进行的"LL旋转"。

LR的旋转代码

/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
    k3.left = rightRightRotation(k3.left);

    return leftLeftRotation(k3);
}

2.4 RL的旋转

RL是与LR的对称情况！RL恢复平衡的旋转方法如下：

第一次旋转是围绕"k3"进行的"LL旋转"，第二次是围绕"k1"进行的"RR旋转"。

RL的旋转代码

/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
    k1.right = leftLeftRotation(k1.right);

    return rightRightRotation(k1);
}

3. 插入

插入节点的代码

当插入的元素存在，这里不做处理

public AvlNode<T> insert(T x,AvlNode<T> t)
{
　　if(t==null)
　　　　return new AvlNode<>(x,null,null);
　　
　　int r=x.compareTo(t.element);
　　if(r<0)
　　　　t.left=insert(x,t.left);
　　else if(r>0)
　　　　t.right=insert(x,t.right);
　　else
　　　　;//重复，不做

　　return balance(t);
}

4. 删除

删除节点的代码

这里用的是懒惰删除。当t没有孩子，则直接删除即可，当t有一个孩子，则用孩子代替此节点即可，当t有两个孩子的时候，用右子树中的最小节点的数据代替t中的数据，但是

t的指针不变，然后删除右子树的那个最小数据节点。（因为t两个孩子时，指针不能改变，所以只能改变数据）

public AvlNode<T> remove(T x,AvlNode<T> t){
　　if(t==null)
　　　　return t;
　　
int r=x.compareTo(t.element);

if(r<0)
　　t.left=remove(x,t.left);
else if(r>0)
　　t.right=remove(x,t.right);
//找到节点以后
else if(t.left!=null&&t.right!=null)//两个儿子
{
　　t.element=findMin(t.right).element;
　　t.right=remove(t.element,t.right);
}
else //一个儿子。这种情况同时也包含了没有孩子的情况。左节点不为空就用左节点代替，如果左节点为空，则用右节点代替，右节点也可能为空。
　　t=(t.left!=null)?t.left:t.right;

return balance(t);

}

balance函数如下：

    public AvlNode<T> balance(AvlNode<T> t){
        if(t==null)
            return t;
        //左子树比右子树高，左右或左左
        if(height(t.left)-height(t.right)==2){
            //左子树的左子树比左子树的右子树高，左左；
            //这里等号是为了单旋转，双旋转也是可以的，单旋简单
　　　　　　　　/*
　　　　　　　　　　等号出现，表示左子树的左子树和左子树的右子树高度相等，但是t的左子树高度大于右子树，所以，这是删除元素造成的。
　　　　　　　　　　插入是不能做成这种情况，因为插入之前就会是不平衡的。这里使用单旋转，简单。
　　　　　　　　*/
            if(height(t.left.left)>=height(t.left.right)){
                t=leftLeftRotation(t);
            }else{
                //左右,双旋转
                t=leftRightRotation(t);
            }
        }else //右子树比左子树高，右右或右左
            if(height(t.right)-height(t.left)==2){
                if(height(t.right.right)>=height(t.right.left))
                    t=rightRightRotation(t);//右右
                else
                    t=rightLeftRotation(t);
            }

        t.height=Math.max(height(t.left), height(t.right))+1;

        return t;
    }

完整代码只要在上面的AvlTree类中将这些方法加入就行了

例子：

1. 新建AVL树

2. 依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中。

2.01 添加3,2
添加3,2都不会破坏AVL树的平衡性。

2.02 添加1
添加1之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

2.03 添加4
添加4不会破坏AVL树的平衡性。

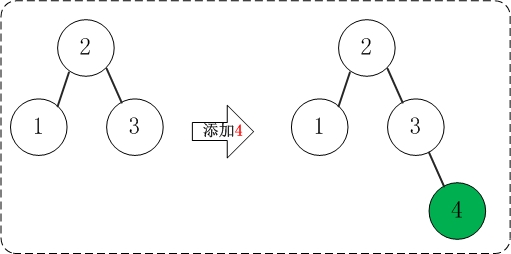
2.04 添加5
添加5之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

2.05 添加6
添加6之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

2.06 添加7
添加7之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

2.07 添加16
添加16不会破坏AVL树的平衡性。

2.08 添加15
添加15之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

2.09 添加14
添加14之后，AVL树失去平衡(RL)，此时需要对AVL树进行旋转(RL旋转)。旋转过程如下：

2.10 添加13
添加13之后，AVL树失去平衡(RR)，此时需要对AVL树进行旋转(RR旋转)。旋转过程如下：

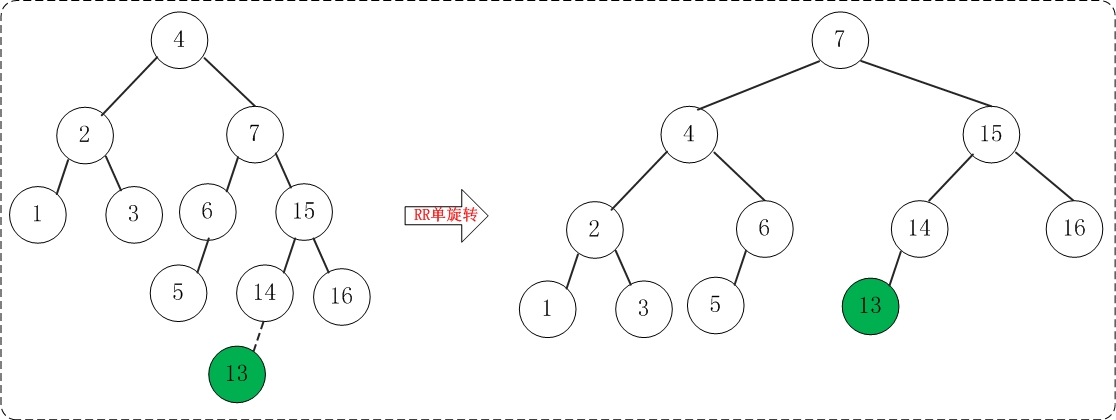
2.11 添加12
添加12之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

2.12 添加11
添加11之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

2.13 添加10
添加10之后，AVL树失去平衡(LL)，此时需要对AVL树进行旋转(LL旋转)。旋转过程如下：

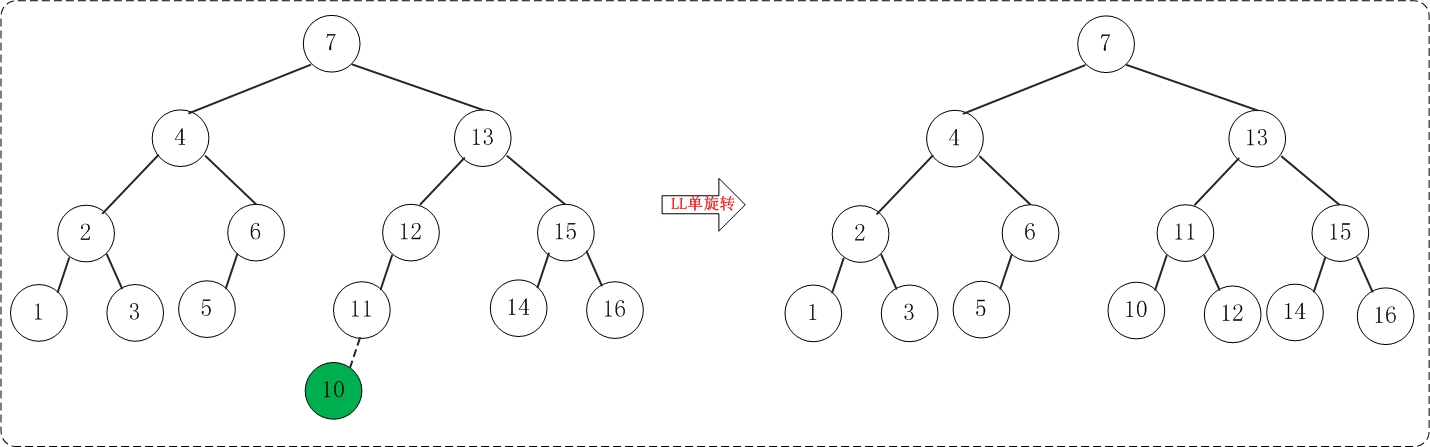
2.14 添加8
添加8不会破坏AVL树的平衡性。

2.15 添加9
但是添加9之后，AVL树失去平衡(LR)，此时需要对AVL树进行旋转(LR旋转)。旋转过程如下：

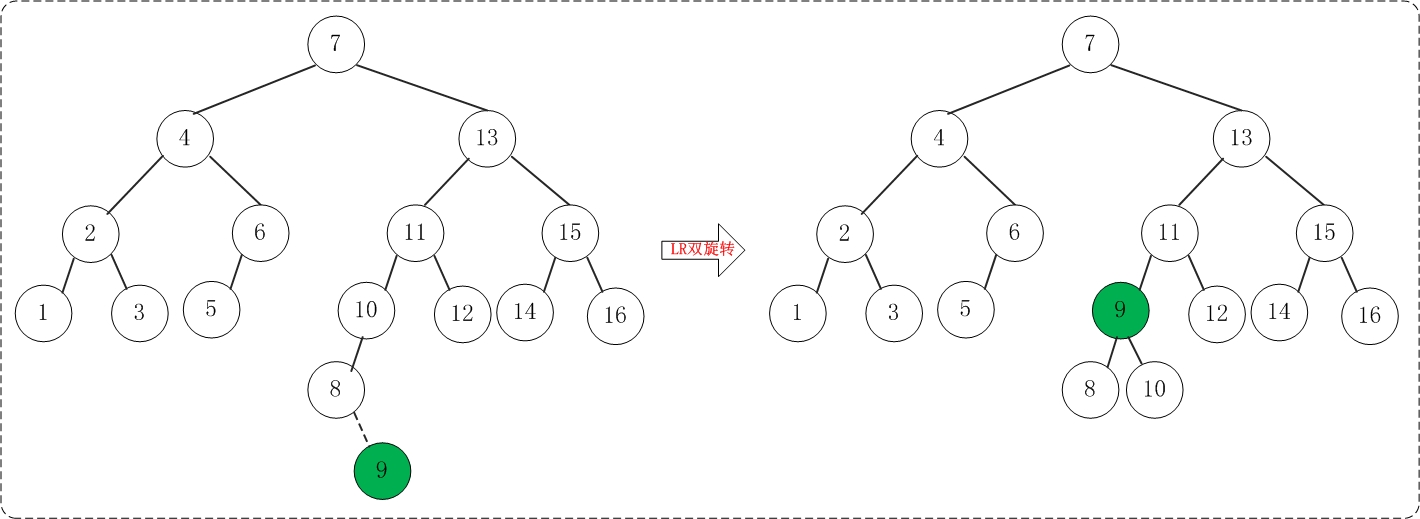
3. 打印树的信息

输出下面树的信息：

前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 
中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 
后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7 
高度: 5
最小值: 1
最大值: 16

4. 删除节点8

删除操作并不会造成AVL树的不平衡。

删除节点8之后，再打印该AVL树的信息。
高度: 5
中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16

转载：http://www.cnblogs.com/skywang12345/p/3577479.html