Eigen学习之简单线性方程与矩阵分解
Eigen提供了解线性方程的计算方法,包括LU分解法,QR分解法,SVD(奇异值分解)、特征值分解等。对于一般形式如下的线性系统:

解决上述方程的方式一般是将矩阵A进行分解,当然最基本的方法是高斯消元法。
先来看Eigen 官方的第一个例程:
#include <iostream>
#include <Eigen/Dense> using namespace std;
using namespace Eigen; int main()
{
Matrix3f A;
Vector3f b;
A << ,,, ,,, ,,;
b << ,,;
cout<<"Here is the Matrix A:\n"<< A <<endl;
cout<<" Here is the vector b:\n"<< b <<endl;
Vector3f x = A.colPivHouseholderQr().solve(b);
cout<<"The solution is:\n"<<x<<endl;
return ;
}
运行结果如下:
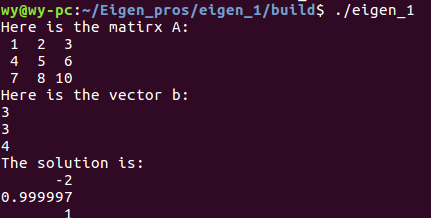
Eigen内置的解线性方程组的算法如下表所示:
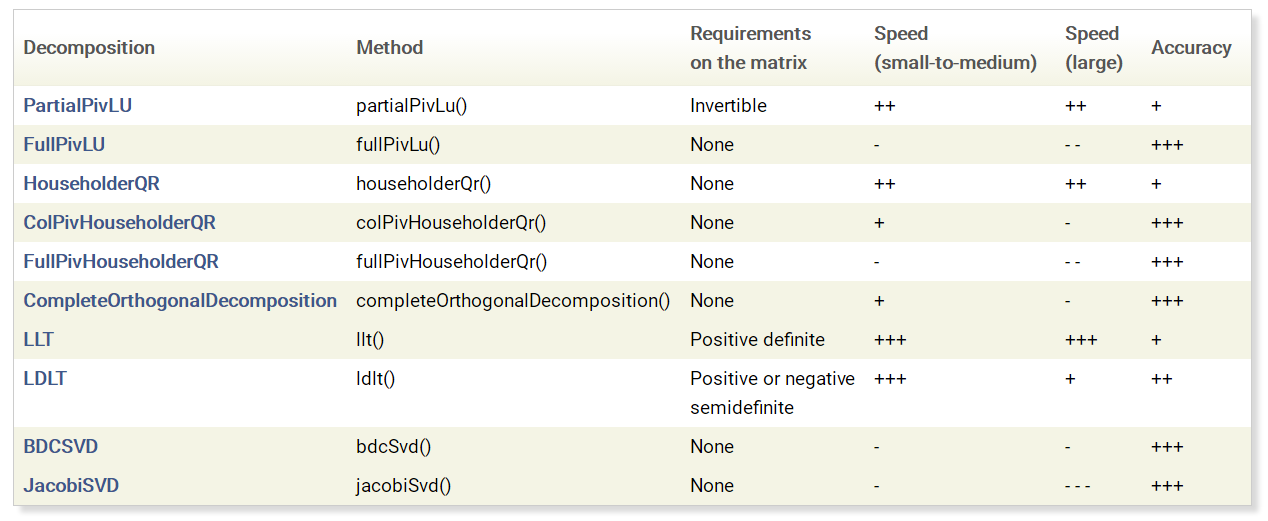
使用这些接口也可以解决矩阵相乘的问题:
#include <iostream>
#include <Eigen/Dense> using namespace std;
using namespace Eigen; int main()
{
Matrix2f A,b;
A << ,-,-,;
b << ,,,;
cout<<"Here is the matrix A:\n"<<A<<endl;
cout<<"Here is the right hand side b:\n"<<b<<endl;
Matrix2f x = A.ldlt().solve(b);
cout<<"The solution is:\n"<<x<<endl;
return ;
}
运行结果如下:

Eigen也提供了计算特征值和特征向量的算法:
下面是一个简单的例子:
#include <iostream>
#include <Eigen/Dense> using namespace std;
using namespace Eigen; int main()
{
Matrix2f A;
A << ,,,;
cout<<"Here is the matrix A:\n"<<A<<endl;
SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
if( eigensolver.info() != Success ) abort();
cout<<" The eigenvalues of A are:\n"<<eigensolver.eigenvalues()<<endl;
cout<<" Here is a matrix whose columns are eigenvectors of A\n"
<<" corresponding to these eigenvalues:\n"
<<eigensolver.eigenvectors()<<endl;
return ;
}
运行结果如下:

Eigen 也提供了求逆矩阵和求矩阵行列式的算法,但是这两种算法对于大型矩阵来说都是非常不经济的算法,当需要对大型矩阵做这种的操作时,需要自己判断到底需不需这样做。但是对于小型矩阵 则可以没有顾虑地使用。
下面是一个例子:
#include <iostream>
#include <Eigen/Dense> using namespace std;
using namespace Eigen; int main()
{
Matrix3f A;
A << ,,,
,,,
-,,; cout<<"Here is the matrix A:\n"<<A<<endl;
cout<<"The determinant of A is "<<A.determinant()<<endl;
cout<<"The inverse of A is:\n"<<A.inverse()<<endl;
return ;
}
运行结果如下:
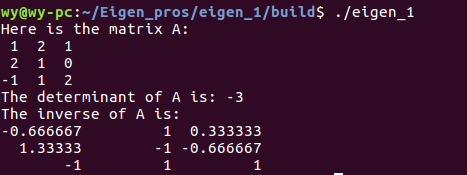
Eigen也提供了解最小二乘问题的解法,并给出两种实现,分别是BDCSVD和JacobiSVD,其中推荐使用的一种是BDCSVD。下面是一个例子:
#include <iostream>
#include <Eigen/Dense> using namespace std;
using namespace Eigen; int main()
{
MatrixXf A = MatrixXf::Random(,);
cout<<"Here is the matrix A:\n"<<A<<endl;
VectorXf b = VectorXf::Random();
cout<<"Here is the right hand side b:\n"<<b<<endl;
cout<<"The least-squares solution is:\n"
<<A.bdcSvd(ComputeThinU|ComputeThinV).solve(b)<<endl;
return ;
}
运行结果如下:
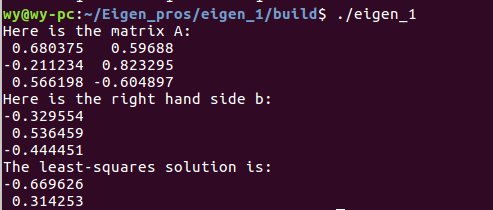
Eigen学习之简单线性方程与矩阵分解的更多相关文章
- 简单的基于矩阵分解的推荐算法-PMF, NMF
介绍: 推荐系统中最为主流与经典的技术之一是协同过滤技术(Collaborative Filtering),它是基于这样的假设:用户如果在过去对某些项目产生过兴趣,那么将来他很可能依然对其保持热忱.其 ...
- 用Spark学习矩阵分解推荐算法
在矩阵分解在协同过滤推荐算法中的应用中,我们对矩阵分解在推荐算法中的应用原理做了总结,这里我们就从实践的角度来用Spark学习矩阵分解推荐算法. 1. Spark推荐算法概述 在Spark MLlib ...
- OpenCV 编程简单介绍(矩阵/图像/视频的基本读写操作)
PS. 因为csdn博客文章长度有限制,本文有部分内容被截掉了.在OpenCV中文站点的wiki上有可读性更好.而且是完整的版本号,欢迎浏览. OpenCV Wiki :<OpenCV 编程简单 ...
- HAWQ + MADlib 玩转数据挖掘之(四)——低秩矩阵分解实现推荐算法
一.潜在因子(Latent Factor)推荐算法 本算法整理自知乎上的回答@nick lee.应用领域:"网易云音乐歌单个性化推荐"."豆瓣电台音乐推荐"等. ...
- FAST MONTE CARLO ALGORITHMS FOR MATRICES II (快速的矩阵分解策略)
目录 问题 算法 LINEARTIMESVD 算法 CONSTANTTIMESVD 算法 理论 算法1的理论 算法2 的理论 代码 Drineas P, Kannan R, Mahoney M W, ...
- ML.NET 示例:推荐之One Class 矩阵分解
写在前面 准备近期将微软的machinelearning-samples翻译成中文,水平有限,如有错漏,请大家多多指正. 如果有朋友对此感兴趣,可以加入我:https://github.com/fei ...
- 矩阵分解----Cholesky分解
矩阵分解是将矩阵拆解成多个矩阵的乘积,常见的分解方法有 三角分解法.QR分解法.奇异值分解法.三角分解法是将原方阵分解成一个上三角矩阵和一个下三角矩阵,这种分解方法叫做LU分解法.进一步,如果待分解的 ...
- RS:关于协同过滤,矩阵分解,LFM隐语义模型三者的区别
项亮老师在其所著的<推荐系统实战>中写道: 第2章 利用用户行为数据 2.2.2 用户活跃度和物品流行度的关系 [仅仅基于用户行为数据设计的推荐算法一般称为协同过滤算法.学术界对协同过滤算 ...
- 【RS】List-wise learning to rank with matrix factorization for collaborative filtering - 结合列表启发排序和矩阵分解的协同过滤
[论文标题]List-wise learning to rank with matrix factorization for collaborative filtering (RecSys '10 ...
随机推荐
- thymeleaf的常见问题汇总
thymeleaf的常见问题汇总 1.thymeleaf th:href 多个参数传递格式 th:href="@{/Controller/update(param1=1,param2=${p ...
- 第5章—构建Spring Web应用程序—关于spring中的validate注解后台校验的解析
关于spring中的validate注解后台校验的解析 在后台开发过程中,对参数的校验成为开发环境不可缺少的一个环节.比如参数不能为null,email那么必须符合email的格式,如果手动进行if判 ...
- 【转】asp.net mvc(模式)和三层架构(BLL、DAL、Model)的联系与区别
原文地址:http://blog.csdn.net/luoyeyu1989/article/details/8275866 首先,MVC和三层架构,是不一样的. 三层架构中,DAL(数据访问层).BL ...
- App实现开机启动
Android启动时,会发出一个系统广播 ACTION_BOOT_COMPLETED,它的字符串常量表示为 “android.intent.action.BOOT_COMPLETED” 开机自启动程序 ...
- java-TreeSet进行排序的2种方式
TreeSet和HashSet的区别在于, TreeSet可以进行排序, 默认使用字典顺序排序, 也可以进行自定义排序 1, 自然排序 2, 比较器排序 自然排序: 1, 需要被排序的类实现Compa ...
- [Hive]使用 Antlr 开发领域语言
Antlr 简介 ANTLR 语言识别的一个工具 (ANother Tool for Language Recognition ) 是一种语言工具,它提供了一个框架,可以通过包含 Java, C++, ...
- C# 在同一个项目里启动不同的类文件
比如有两个类文件分别为 Person.cs 和 Enum.cs : using System; using person; namespace HelloWorld { class HelloWorl ...
- C# 分页方法
using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Web; ...
- mssql名词解释
因为自己在sql这部分不强,有时候碰到一些名词我都不知道什么意思,所以在这里记录下,方便以后查看 1.NOT FOR REPLICATION 控制约束.标志和触发器 在所有IDENTITY属性字段 ...
- [C语言] 数据结构-预备知识动态内存分配
动态内存分配 静态内存分配数组 int a[5]={1,2,3,4,5} 动态内存分配数组 int len=5; int *parr=(int *)malloc(sizeof(int) * len) ...
