自然语言处理词向量模型-word2vec

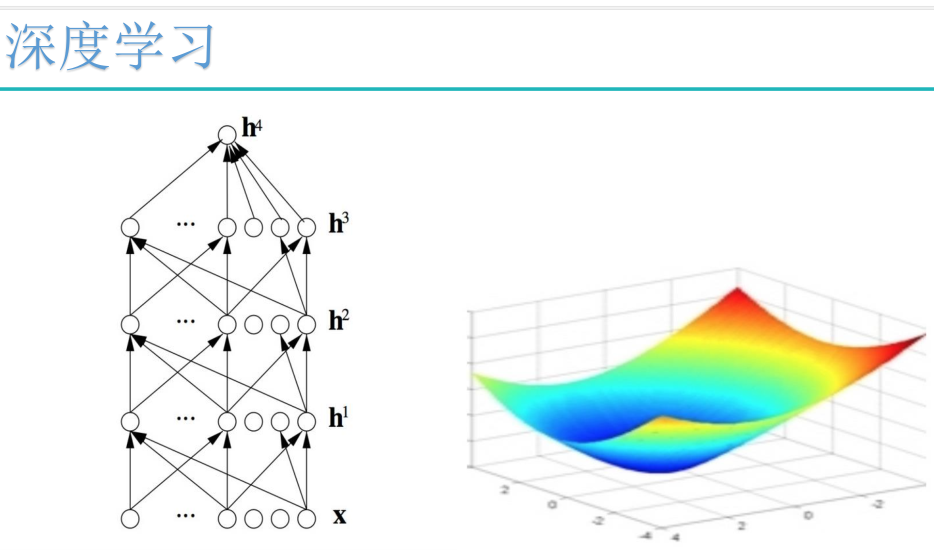
自然语言处理与深度学习：

语言模型：

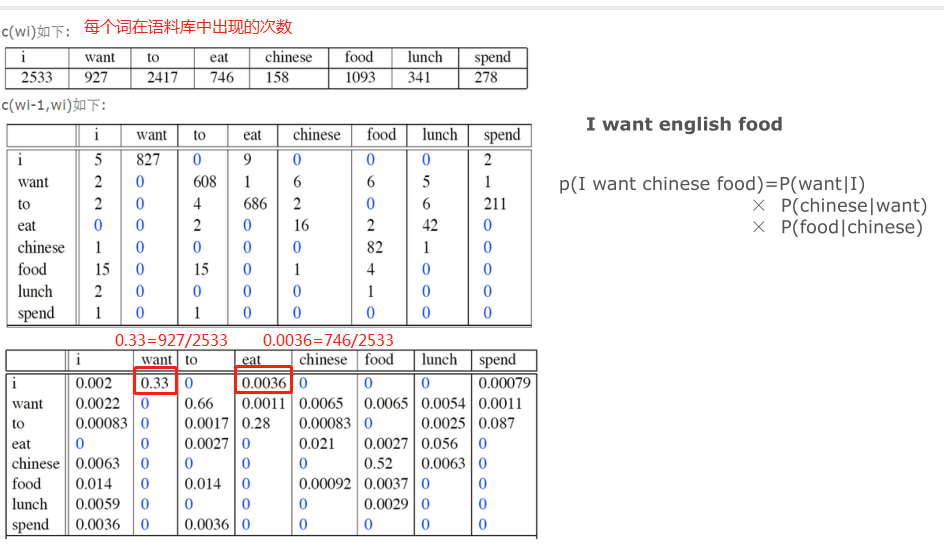
N-gram模型：

N-Gram模型：在自然语言里有一个模型叫做n-gram，表示文字或语言中的n个连续的单词组成序列。在进行自然语言分析时，使用n-gram或者寻找常用词组，可以很容易的把一句话分解成若干个文字片段

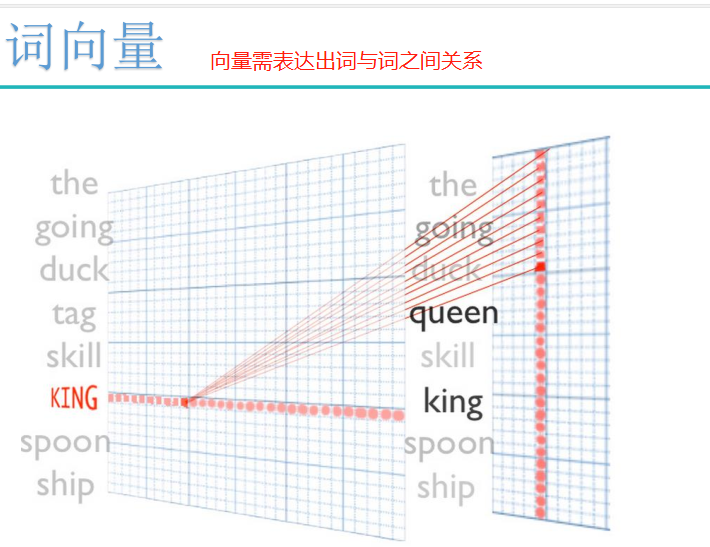
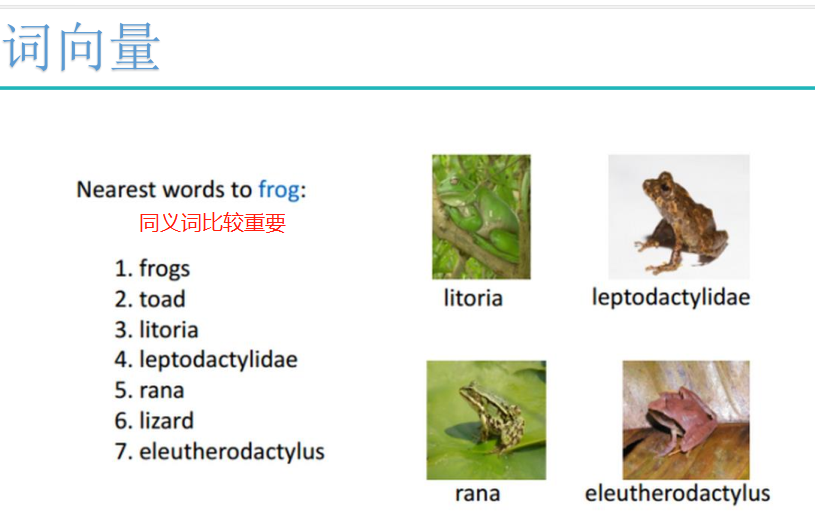
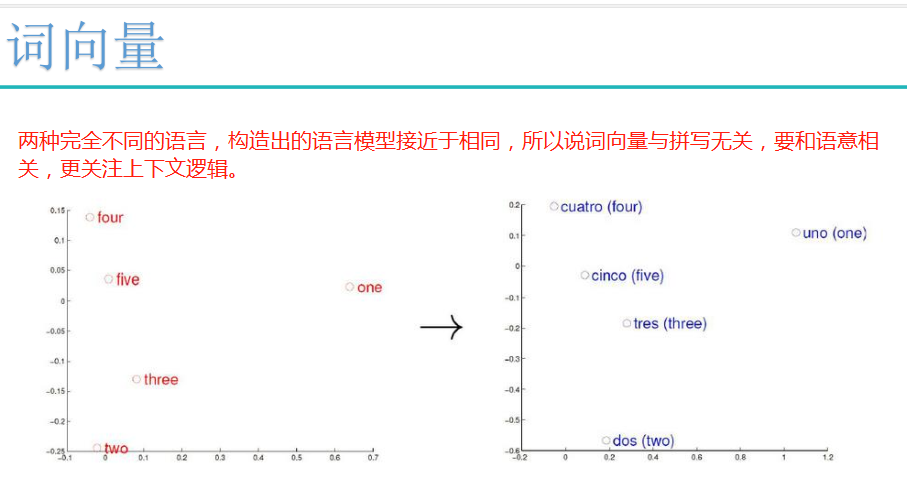
词向量：

神经网络模型：

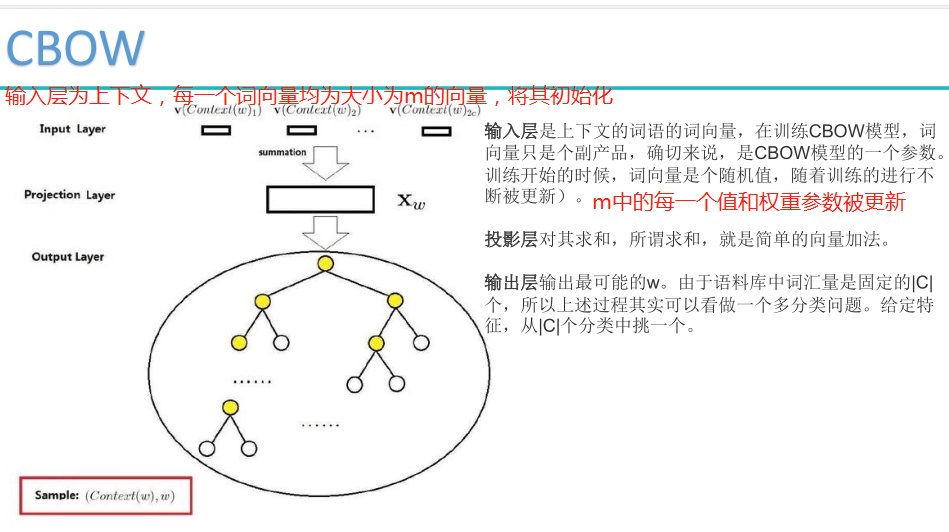
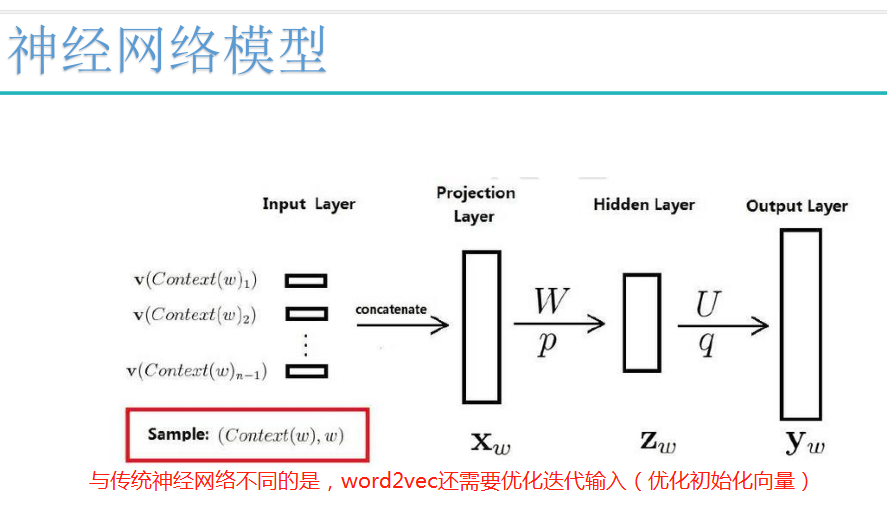注：初始化向量，可以先随机初始化。

传统神经神经网络只需要优化输入层与隐层，隐层与输出层之间的参数。

神经网络模型的优势：一方面可以得到词语之间近似的含义，另一方面求解出的空间符合真实逻辑规律

CBOW求解目标：

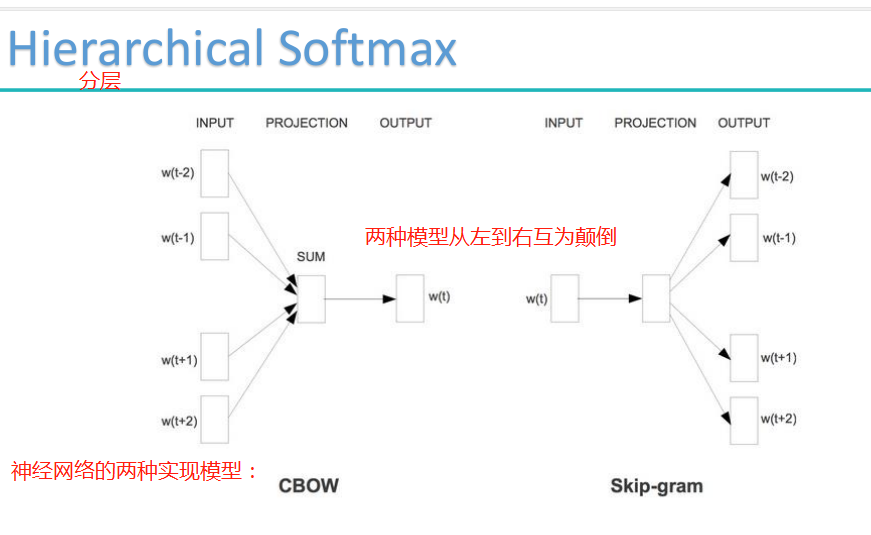
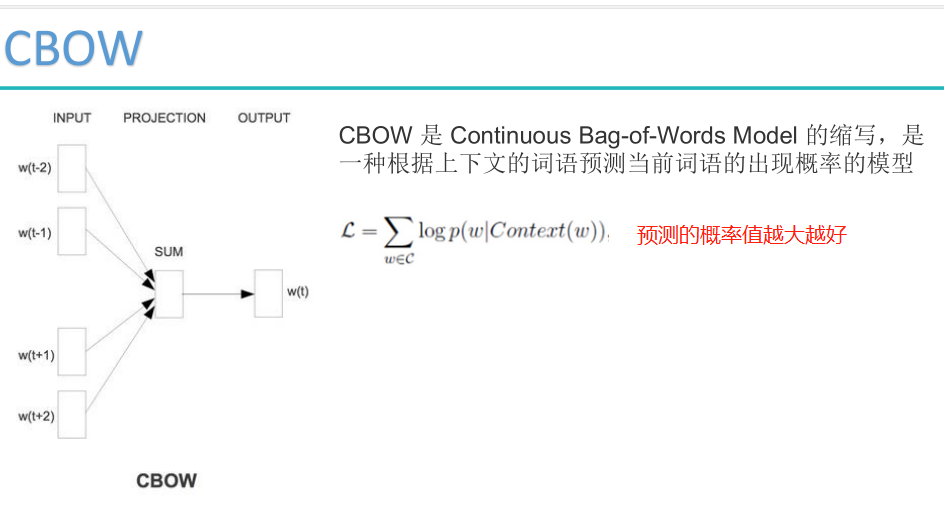
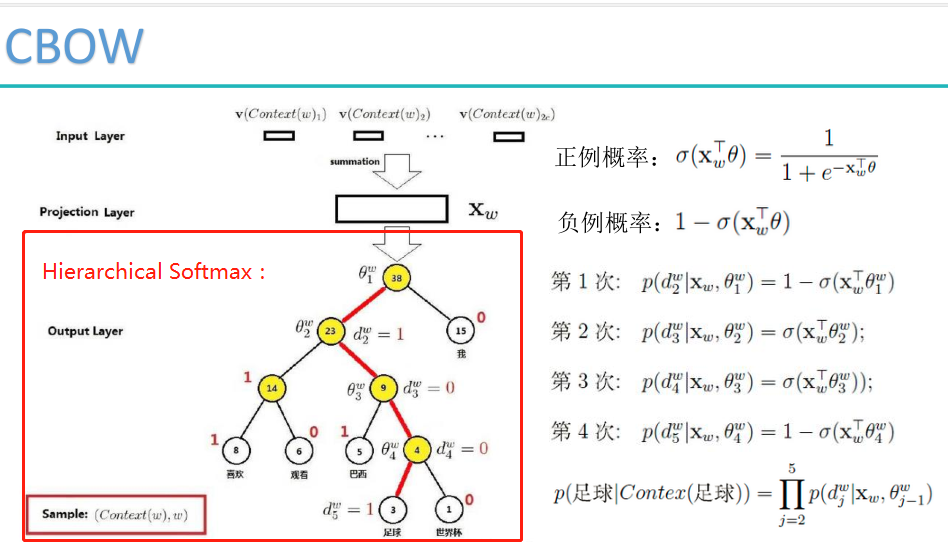
预备知识：

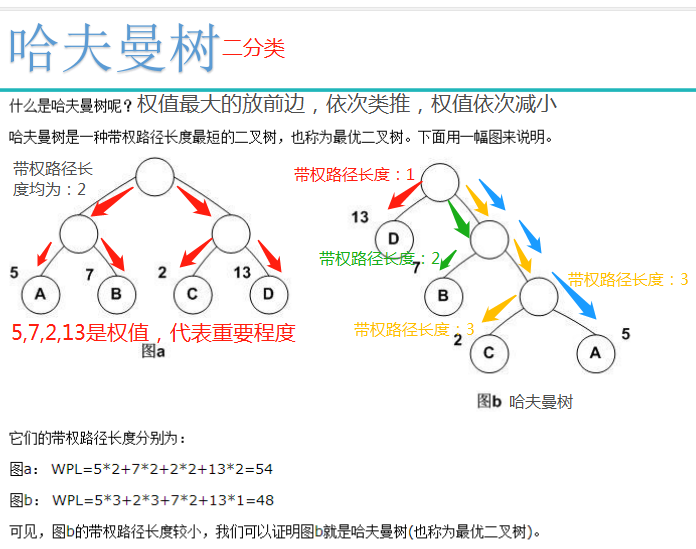
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。

分层的softmax设计思想：词频中出现词概率高的尽可能往前放，可以用哈夫曼树来设计。

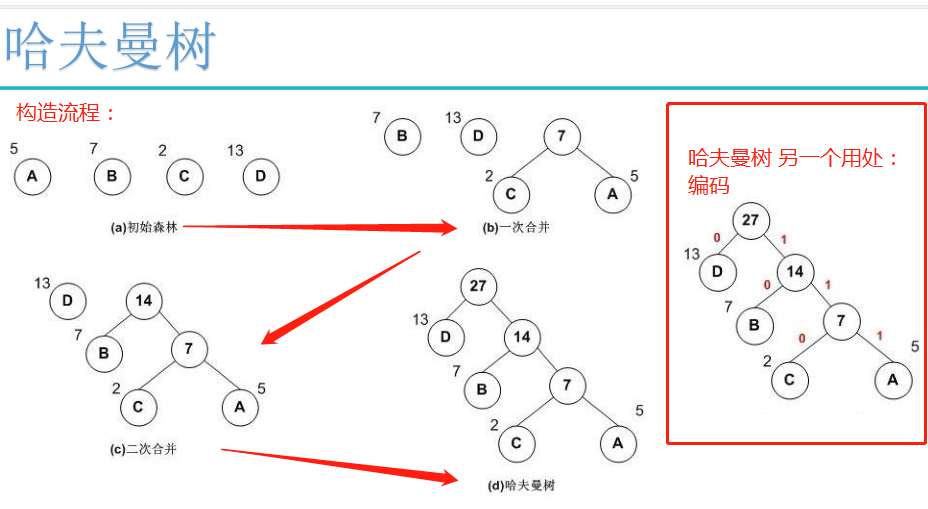
自然语言哈夫曼树详解，包含构造和编码：https://blog.csdn.net/shuangde800/article/details/7341289

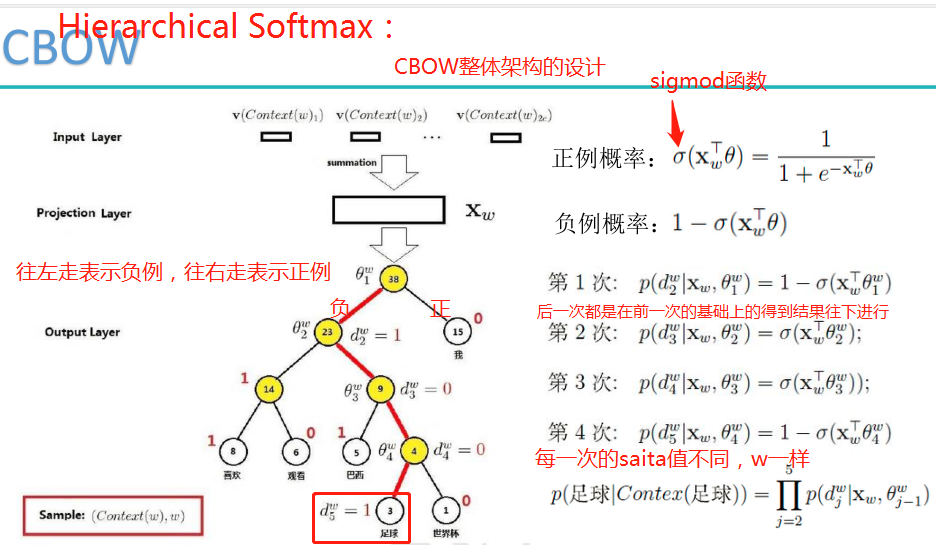
Hierarchical Softmax是用哈夫曼树构造出很多个二分类。

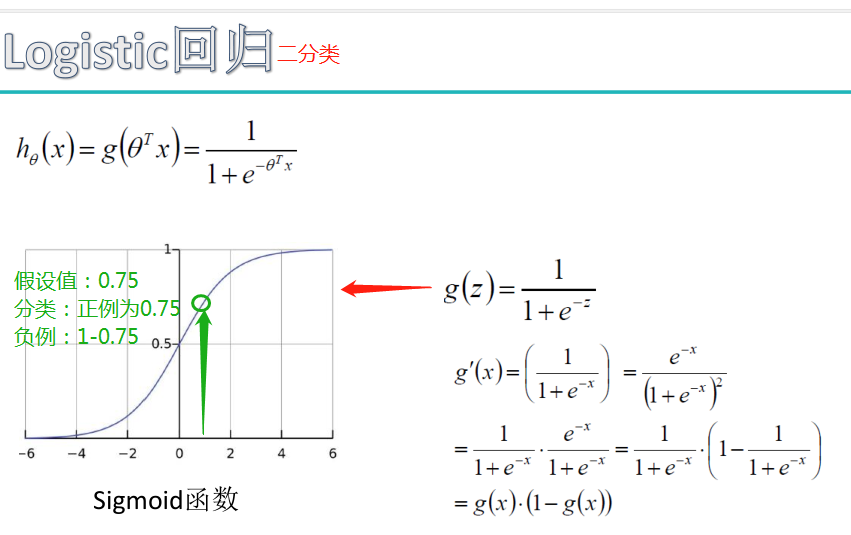
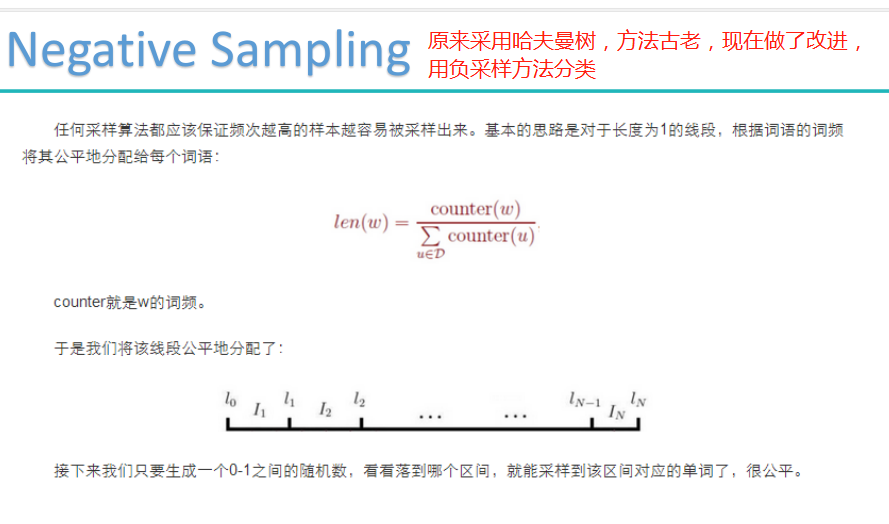
负采样模型：