bzoj千题计划141：bzoj3532: [Sdoi2014]Lis

http://www.lydsy.com/JudgeOnline/problem.php?id=3532

如果没有字典序的限制，那么DP拆点最小割即可

加上字典序的限制：

按c从小到大枚举最小割边集中的边，去掉这条边对网络的影响，继续枚举直至获得最小割边集

判断是不是最小割边集中的边：

在残量网络中边的起点和终点不连通

注：最小割边集中的边一定满流，但满流边不一定是最小割边集中的边

如下图所示，流量为1和3的两条边满流，但最小割边集为流量为4的那条边

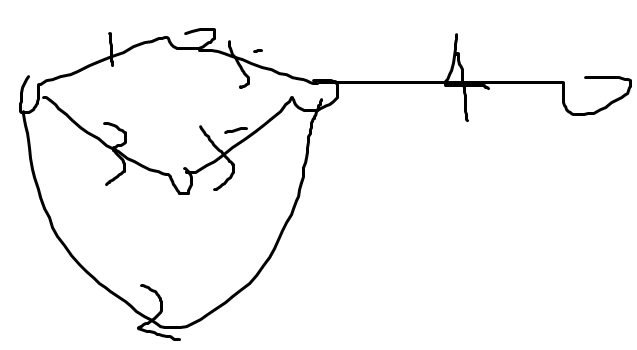
去掉一条边对网络的影响：

边：u-->v

这条边的流量和反向弧的流量置为0

在残量网络上，汇点向v跑一遍最大流，u向源点跑一遍最大流

判断已经得到了最小割中的所有边：

残量网络上，源点和汇点不连通

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 1410
#define M 520000
const int inf=2e9;

int n;
int a[N],b[N],c[N];

int f[N];

int tot;
int front[N],nxt[M<<],to[M<<],val[M<<],from[M<<];
int lev[N],num[N];
int path[N];
int cur[N];

int src,decc;

int id[N];
bool use[N];
int cnt[N];

int all;

int ans[N];

bool vis[N];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c))  c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar();  }
}

void add(int u,int v,int w)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; from[tot]=u; val[tot]=w;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; from[tot]=v; val[tot]=;
   // cout<<u<<' '<<v<<' '<<w<<'\n';
}

bool bfs()
{
    queue<int>q;
    for(int i=;i<=all;++i) lev[i]=all;
    q.push(decc);
    lev[decc]=;
    int now,t;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        for(int i=front[now];i;i=nxt[i])
        {
            t=to[i];
            if(lev[t]==all && val[i^])
            {
                lev[t]=lev[now]+;
                q.push(t);
            }
        }
    }
    return lev[src]!=all;
}

int augment()
{
    int now=decc,flow=inf;
    int i;
    while(now!=src)
    {
        i=path[now];
        flow=min(flow,val[i]);
        now=from[i];
    }
    now=decc;
    while(now!=src)
    {
        i=path[now];
        val[i]-=flow;
        val[i^]+=flow;
        now=from[i];
    }
    return flow;
}

void isap()
{
    int flow=;
    if(!bfs()) return ;
    memset(num,,sizeof(num));
    for(int i=;i<=all;++i) num[lev[i]]++,cur[i]=front[i];
    int now=src,t;
    while(lev[src]<all)
    {
        if(now==decc)
        {
            flow+=augment();
            now=src;
        }
        bool advanced=false;
        for(int i=cur[now];i;i=nxt[i])
        {
            t=to[i];
            if(lev[t]==lev[now]- && val[i])
            {
                advanced=true;
                path[t]=i;
                cur[now]=i;
                now=t;
                break;
            }
        }
        if(!advanced)
        {
            int mi=all;
            for(int i=front[now];i;i=nxt[i])
                if(val[i]) mi=min(mi,lev[to[i]]);
            if(!--num[lev[now]]) break;
            num[lev[now]=mi+]++;
            cur[now]=front[now];
            if(now!=src) now=from[path[now]];
        }
    }
   // cout<<flow<<'\n';
}

void build()
{
    src=; decc=(n<<|)+;
    int mx,max_len=;
    for(int i=n;i;--i)
    {
        mx=;
        for(int j=i+;j<=n;++j)
            if(a[j]>a[i]) mx=max(mx,f[j]);
        f[i]=mx+;
        max_len=max(max_len,f[i]);
    }
    tot=;
    memset(front,,sizeof(front));
    for(int i=;i<=n;++i)
    {
        id[i]=tot+;
        add(i<<,i<<|,b[i]);
    }
    for(int i=;i<=n;++i)
        if(f[i]==max_len) add(src,i<<,inf);
    for(int i=;i<=n;++i)
        if(f[i]==) add(i<<|,decc,inf);
    for(int i=;i<=n;++i)
        for(int j=i+;j<=n;++j)
            if(a[j]>a[i] && f[i]==f[j]+) add(i<<|,j<<,inf);
}

bool find(int u,int v)
{
    memset(vis,false,sizeof(vis));
    queue<int>q;
    q.push(u);
    vis[u]=true;
    int now,t;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        for(int i=front[now];i;i=nxt[i])
        {
            if(!val[i]) continue;
            t=to[i];
            if(!vis[t])
            {
                vis[t]=true;
                q.push(t);
            }
        }
    }
    return vis[v];
}

void solve()
{
    int sum=,num=;
    int mi;
    c[]=inf;
    memset(use,false,sizeof(use));
    while()
    {
        mi=;
        for(int i=;i<=n;++i)
            if(!val[id[i]] && !use[i] && c[mi]>c[i]) mi=i;
        use[mi]=true;
        if(find(from[id[mi]],to[id[mi]])) continue;
        ans[++num]=mi;
        sum+=b[mi];
        val[id[mi]]=val[id[mi]+]=;
        src=all; decc=mi<<|;
        isap();
        src=mi<<; decc=;
        isap();
        src=all; decc=;
        if(!bfs()) break;
    }
    cout<<sum<<' '<<num<<'\n';
    sort(ans+,ans+num+);
    for(int i=;i<num;++i) cout<<ans[i]<<' ';
    cout<<ans[num]<<'\n';
}

int main()
{
    int T;
    read(T);
    while(T--)
    {
        read(n);
        all=(n<<|)+;
        for(int i=;i<=n;++i) read(a[i]);
        for(int i=;i<=n;++i) read(b[i]);
        for(int i=;i<=n;++i) read(c[i]);
        build();
        isap();
        solve();
    }
}

3532: [Sdoi2014]Lis

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 977  Solved: 362
[Submit][Status][Discuss]

Description

给定序列A，序列中的每一项Ai有删除代价Bi和附加属性Ci。请删除若
干项，使得4的最长上升子序列长度减少至少1，且付出的代价之和最小，并输出方案。
    如果有多种方案，请输出将删去项的附加属性排序之后，字典序最小的一种。

Input

输入包含多组数据。
    输入的第一行包含整数T，表示数据组数。接下来4*T行描述每组数据。
    每组数据的第一行包含一个整数N，表示A的项数，接下来三行，每行N个整数A1．．An，B1．，Bn，C1．．Cn，满足1 < =Ai，Bi，Ci < =10^9，且Ci两两不同。

Output

对每组数据，输出两行。第一行包含两个整数S，M，依次表示删去项的代价和与数量；接下来一行M个整数，表示删去项在4中的的位置，按升序输出。

Sample Input

1
6
3 4 4 2 2 3
2 1 1 1 1 2
6 5 4 3 2 1

Sample Output

4 3
2 3 6
解释：删去(A2，43，A6)，(A1，A6)，(A2，43，44，A5)等都是合法的方案，但
{A2，43，A6)对应的C值的字典序最小。

HINT

1 < =N < =700     T < =5