HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm

HyperLogLog参考下面这篇blog，

http://blog.codinglabs.org/articles/algorithms-for-cardinality-estimation-part-iv.html

为何LLC在基数不大的时候会误差比较大？
直观上，由于基数不大时，会有很多空桶，而最终结果是求平均值，这个值对离群值（这里的0）非常敏感
那么重理论上看，为何误差比较大？
LLC的渐近标准误差为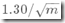 ，看上去只是和桶数m有关，为何还和基数大小有关？
关键就是理解渐近标准误差，
标准误差，（个人理解）
对于估计，真实值和预测值之间一定有误差的，这种误差往往符合高斯分布（根据中心极限定理）
而高斯分布的参数 ，就是表示标准误差，因为这个参数表示高斯分布的宽窄，所以 越小，表示高斯分布越收拢，即越多的预测值会更接近均值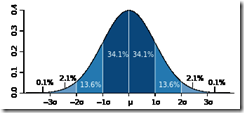

所以标准误差是可以用来衡量模型预测质量好坏的，所以如果LLC的标准误差为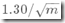，那么该算法的误差只和桶数m相关
但是这里“渐近”两个字，表示只有当基数n趋向于无穷大，标准差才趋向于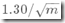
这就解释了前面的问题

所以解决这个问题两个改进算法，

Adaptive Counting，简单的想法，在n比较小的时候使用linear counting，n比较大的时候用LLC
HyperLogLog Counting，比较复杂的方法，参考“HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm”
基本的改进是使用调和平均数替代几何平均数，以减少对离群值的敏感性

 

---------------------------------------------------------------------------------------------------------------------------------------------------------------

传统的cardinality统计的方法过于耗费内存, 所以有很多近似的方法以比较低的资源耗费来解决这个问题
在Goolge，每天都会有如下数据分析系统需要对非常大的数据集做cardinality估计，所以google对HyperLogLog做了一系列的improvement。

At Google, various data analysis systems such as Sawzall [15], Dremel [13] and PowerDrill [9] estimate the cardinality of very large data sets every day, for example to determine the number of distinct search queries on google.com over a time period.

 

Google做了一系列的实验对比，从准确率上来看，Linear counting是最好的，所以当数据量不大的时候首选
但是当基数的取值很大的时候，空间效率上看是有问题的，所以还是选择准确率稍差的HLLC

算法设计的Goal是，

Therefore, the key requirements for a cardinality estimation algorithm can be summarized as follows:
• Accuracy.
  For a fixed amount of memory, the algorithm should provide as accurate an estimate as possible. Especially for small cardinalities, the results
should be near exact.
• Memory efficiency.
  The algorithm should use the available memory efficiently and adapt its memory usage to the cardinality. That is, the algorithm should use less
than the user-specified maximum amount of memory if the cardinality to be estimated is very small.
• Estimate large cardinalities.
  Multisets with cardinalities well beyond 1 billion occur on a daily basis, and it is important that such large cardinalities can be estimated with reasonable accuracy.
• Practicality.
  The algorithm should be implementable and maintainable.

 

HLLC算法

相对于LLC的n的公式，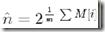

HLLC前面的步骤都是一样，只是最后的计算公式，用调和平均数

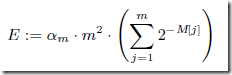  ，其中

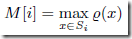
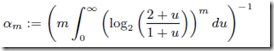
并且在实现的时候做了如下的优化，主要是指n很小和很大时，做些特殊化处理

1. Initialization of registers.
The registers are initialized to 0 instead of to avoid the result 0 for n << mlogm where n is the cardinality of the data stream (i.e., the value we are trying to estimate).

2. Small range correction.
Simulations by Flajolet et. al. show that for  nonlinear distortions appear that need to be corrected.
Thus, for this range LinearCounting [16] is used.

3. Large range corrections.
When n starts to approach , hash collisions become more and more likely (due to the 32 bit hash function). To account for this, a correction is used.

 

Google对HLLC的提高

1. Using a 64 Bit Hash Function
这个很容易理解，google需要处理的cardinalities beyond 1 billion，所以原来的32bit不够

 

2.Estimating Small Cardinalities
对于很小的cardinalities，之前的处理是，当就使用Linear counting

这里提出一种bias-corrected的方法，文章中实验如下，

 
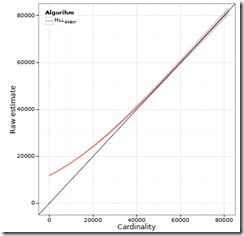
Our experiments show that at the latest for n > 5m the correction does no longer reduce the error significantly.

所以在n> 5m的时候，直接用HLLC就ok
但是当n<5m时，文章中试图用他们的实验数据去把bias修正掉

再次测试结果是，尽管这样，在n很小的情况下，仍然是Linear counting的效果比较好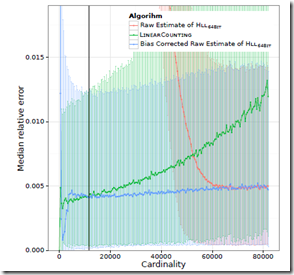

所以最终的逻辑是

当n<5m时，会优先使用bias-corrected的方法， 只有当出现空桶，即n很小的情况下，才使用linear counting

3.Sparse Representation

这组优化关键就是更加节省空间，其实HLLC对空间的耗费本身就不高，但是由于google的基数实在太大导致桶数也非常大， 所以再小的值乘上个超大的基数也扛不住

优化都比较简单，

1. 当n<<m，情况下，即有很多空桶，那不用记录每个桶的情况，只需要记录有数据的桶，就是稀疏表示，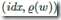
2. 在稀疏表示的情况下，可以使用更多位数来表示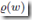 ，以达到更高的precision

3. 进一步压缩稀疏表示

4. 在linear counting的情况下，其实不需要记录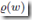

 

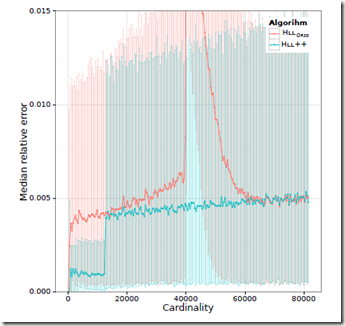
最终HLLC和google的HLLC++的数据对比