HDU1796How many integers can you find（容斥原理）

在计数时，必须注意无一重复，无一遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

（1）两个集合容斥关系

（2）三个集合容斥关系

公式：

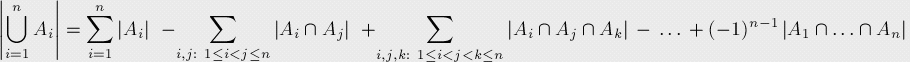
这就是所谓的奇加偶减。

贴个模版题：

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1796

题目解析：

这个题有bug,m可能为0。然后知道奇加偶减这个东西后，就可以深搜了，将所有组合情况全列出来，然后求lcm就好了。

求1~（n-1)中被集合m中元素中整除的个数，没学容斥原理之前做这题肯定是会超时的。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
int n,m,top;
__int64 a[];
int gcd(int A,int B)
{
    return B==?A:gcd(B,A%B);
}
//now为当前点，num为已经加入容斥的个数，lcm记录容斥的过程值（lcm），结果
void dfs(int now,int num,__int64 lcm,__int64 &sum)
{
    lcm=a[now]/gcd(a[now],lcm)*lcm;
    if(num&) sum+=(n-)/lcm;
    else sum-=(n-)/lcm;
    for(int i=now+; i<top; i++)
        dfs(i,num+,lcm,sum);
}
int main()
{
    int xx;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        top=;
        for(int i=; i<m; i++)
        {
            scanf("%d",&xx);
            if(xx!=)
            {
                a[top++]=xx;
            }
        }
        __int64 sum=;
        for(int i=; i<top; i++)
        {
            dfs(i,,a[i],sum);
        }
        printf("%I64d\n",sum);
    }
    return ;
}