CF Round946 (Div. 3)A

Phone Desktop

题目描述

Little Rosie has a phone with a desktop (or launcher, as it is also called). The desktop can consist of several screens. Each screen is represented as a grid of size $ 5 \times 3 $ , i.e., five rows and three columns.

There are $ x $ applications with an icon size of $ 1 \times 1 $ cells; such an icon occupies only one cell of the screen. There are also $ y $ applications with an icon size of $ 2 \times 2 $ cells; such an icon occupies a square of $ 4 $ cells on the screen. Each cell of each screen can be occupied by no more than one icon.

Rosie wants to place the application icons on the minimum number of screens. Help her find the minimum number of screens needed.

输入格式

The first line of the input contains $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases.

The first and only line of each test case contains two integers $ x $ and $ y $ ( $ 0 \leq x, y \leq 99 $ ) — the number of applications with a $ 1 \times 1 $ icon and the number of applications with a $ 2 \times 2 $ icon, respectively.

输出格式

For each test case, output the minimal number of required screens on a separate line.

样例 #1

样例输入 #1

11
1 1
7 2
12 4
0 3
1 0
8 1
0 0
2 0
15 0
8 2
0 9

样例输出 #1

1
1
2
2
1
1
0
1
1
2
5

提示

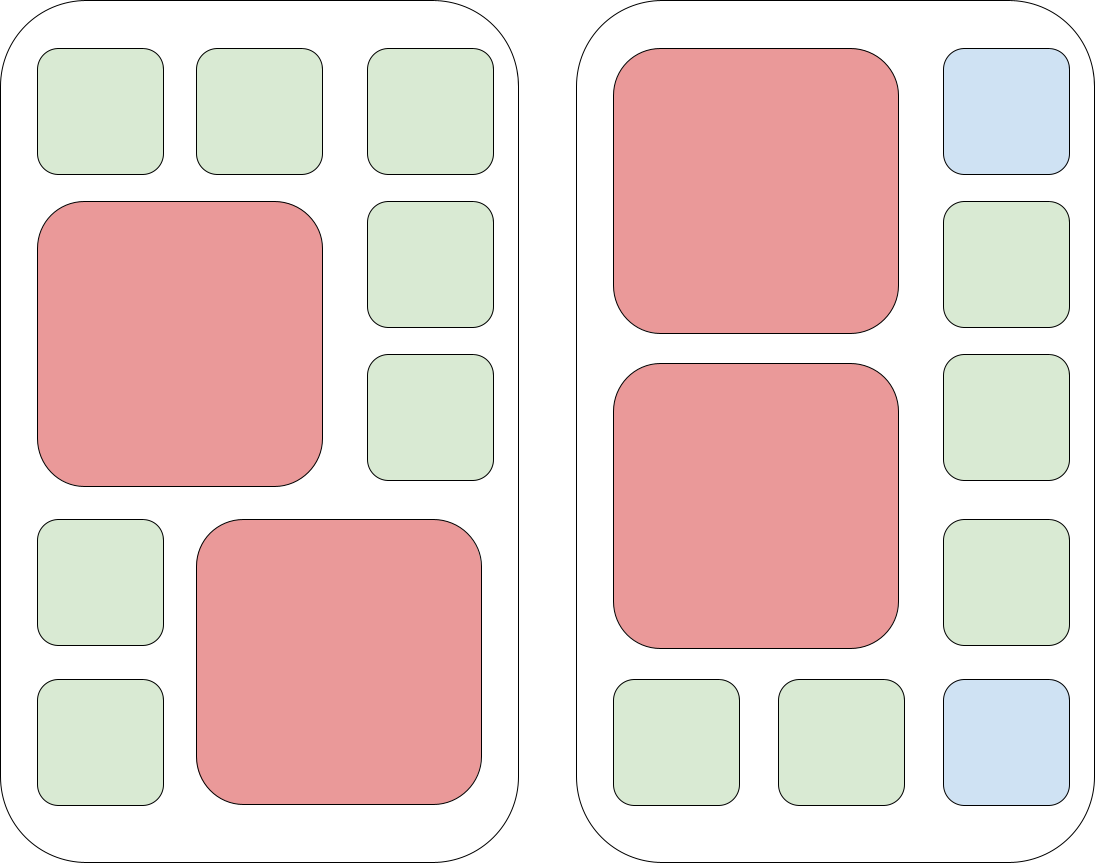
The solution for the first test case can look as follows:

Blue squares represent empty spaces for icons, green squares represent $ 1 \times 1 $ icons, red squares represent $ 2 \times 2 $ iconsThe solution for the third test case can look as follows:

AC_code

本人丑陋的模拟写法

#include <iostream>

using namespace std;

int _;
int x, y;
int sum ,d;

int main()
{
    cin >> _;
    while(_ --) {
        cin >> x >> y;
        sum = 0;

        d = y / 2;
        sum += 7 * d;
        if(y % 2 != 0) sum += 11, d += 1;

        if(x <= sum) cout << d << endl;
        else {
            x -= sum;
            int f = 0;
            while(x > 0) {
                x -= 15, ++ f;
            }
            cout << d + f << endl;
        }
    }

    return 0;
}

听完题解get到写法

#include <iostream>

using namespace std;

int _;
int x, y, d, sum;

void solve() {
    d = (y + 1) / 2;//上取整
    if(x > d * 15 - y * 4) {
        x -= d * 15 - y * 4;
        d += (x + 1) / 15;//上取整
    }
    cout << d << endl;
}

int main()
{
    cin >> _;
    while(_ -- ) {
        cin >> x >> y;
        solve();
    }
    return 0;
}

get到技能：上取整(分母 - 1)

分母 - 1再除以除数

int x = 310;
cout << (x + 14) / 15;//通常使用比除数更小1的数构造上取整

复习：先将一个数变为正数再取模

正数返回本身，负数变为正数再取模

int x = -6;
cout << (x + 10) % 10 << endl;

贪心：先猜22，再猜11

#include <bits/stdc++.h>

using i64 = long long;

void solve() {
    int x, y;
    std::cin >> x >> y;

    int ans = std::max((y + 1) / 2, (x + 4 * y + 14) / 15);
    std::cout << ans << "\n";
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;

    while(t --) {
        solve();
    }
    return 0;
}

后记

蒟蒻第一场CF(div3)被按在地上摩擦，只Ac了一题，第二题构造映射被卡，接下来决定加训疯狂补题T.T，第一次交题不注意还交错文件了

码力超弱，写个模拟题都花费大量时间