经典的损失函数：

①交叉熵（分类问题）：判断一个输出向量和期望向量有多接近。交叉熵刻画了两个概率分布之间的距离，他是分类问题中使用比较广泛的一种损失函数。概率分布刻画了不同事件发生的概率。

熵的定义：解决了对信息的量化度量问题，香农用信息熵的概念来描述信源的不确定度，第一次用数学语言阐明了概率与信息冗余度的关系。

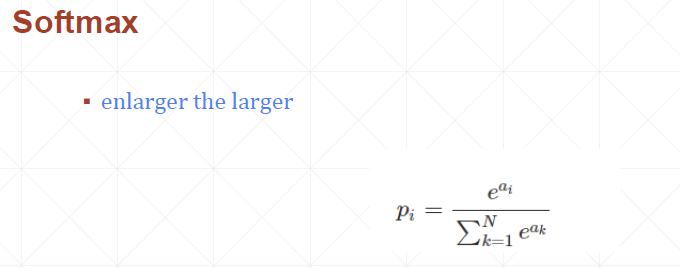
 从统计方面看交叉熵损失函数的含义：

Softmax：原始神经网路的输出被作用在置信度来生成新的输出，新的输出满足概率分布的所有要求。这样就把神经网络的输出变成了一个概率分布，从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离。

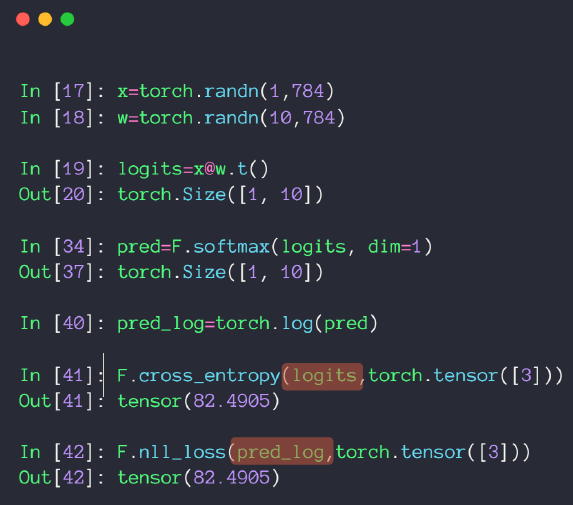
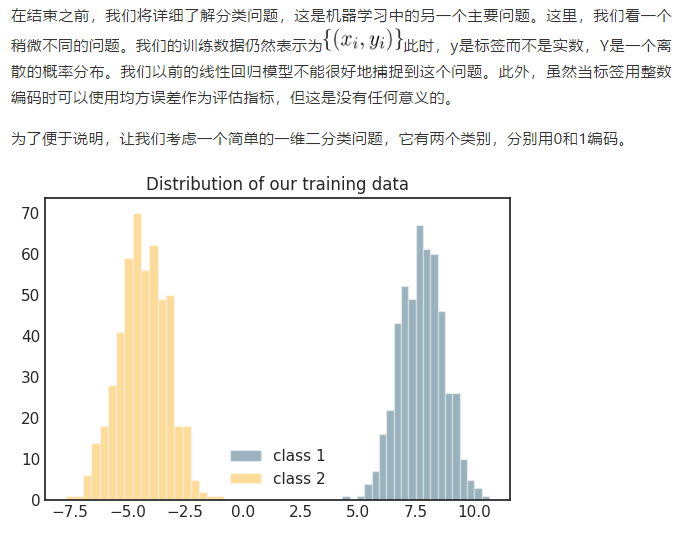
②回归问题解决的是对具体数值的预测。这些问题需要预测的不是一个事先定义好的类别，而是一个任意的实数。解决回归问题的神经网络一般只有一个输出结点，这个结点的输出值就是预测值。对于回归问题，最常用的损失函数就是均方误差（MSE，mean squared error）:

经典的损失函数：交叉熵和MSE的更多相关文章

  1. 机器学习之路：tensorflow 深度学习中 分类问题的损失函数 交叉熵

    经典的损失函数----交叉熵 1 交叉熵: 分类问题中使用比较广泛的一种损失函数, 它刻画两个概率分布之间的距离 给定两个概率分布p和q, 交叉熵为: H(p, q) = -∑ p(x) log q( ...

  2. TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵

    TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵 神经元模型:用数学公式比表示为:f(Σi xi*wi + b), f为激活函数 神经网络 是以神经元为基本单位构成的 激 ...

  3. [ch03-02] 交叉熵损失函数

    系列博客,原文在笔者所维护的github上:https://aka.ms/beginnerAI, 点击star加星不要吝啬,星越多笔者越努力. 3.2 交叉熵损失函数 交叉熵(Cross Entrop ...

  4. 【深度学习】softmax回归——原理、one-hot编码、结构和运算、交叉熵损失

    1. softmax回归是分类问题 回归(Regression)是用于预测某个值为"多少"的问题,如房屋的价格.患者住院的天数等. 分类(Classification)不是问&qu ...

  5. 第五节，损失函数：MSE和交叉熵

    损失函数用于描述模型预测值与真实值的差距大小,一般有两种比较常见的算法——均值平方差(MSE)和交叉熵. 1.均值平方差(MSE):指参数估计值与参数真实值之差平方的期望值. 在神经网络计算时,预测值 ...

  6. 经典损失函数：交叉熵（附tensorflow）

    每次都是看了就忘,看了就忘,从今天开始,细节开始,推一遍交叉熵. 我的第一篇CSDN,献给你们(有错欢迎指出啊). 一.什么是交叉熵 交叉熵是一个信息论中的概念,它原来是用来估算平均编码长度的.给定两 ...

  7. 深度学习原理与框架-神经网络结构与原理 1.得分函数 2.SVM损失函数 3.正则化惩罚项 4.softmax交叉熵损失函数 5. 最优化问题(前向传播) 6.batch_size(批量更新权重参数) 7.反向传播

    神经网络由各个部分组成 1.得分函数:在进行输出时,对于每一个类别都会输入一个得分值,使用这些得分值可以用来构造出每一个类别的概率值,也可以使用softmax构造类别的概率值,从而构造出loss值, ...

  8. 【联系】二项分布的对数似然函数与交叉熵（cross entropy）损失函数

    1. 二项分布 二项分布也叫 0-1 分布,如随机变量 x 服从二项分布,关于参数 μ(0≤μ≤1),其值取 1 和取 0 的概率如下: {p(x=1|μ)=μp(x=0|μ)=1−μ 则在 x 上的 ...

  9. 【机器学习基础】交叉熵（cross entropy）损失函数是凸函数吗？

    之所以会有这个问题,是因为在学习 logistic regression 时,<统计机器学习>一书说它的负对数似然函数是凸函数,而 logistic regression 的负对数似然函数 ...

随机推荐

  1. JavaWeb和WebGIS学习笔记（三）——GeoServer 发布shp数据地图

    系列链接: Java web与web gis学习笔记(一)--Tomcat环境搭建 Java web与web gis学习笔记(二)--百度地图API调用 JavaWeb和WebGIS学习笔记(三)-- ...

  2. PostgreSQL培训认证讲师招募

    中国PostgreSQL考试认证中心 以"知"之名,携手共进!不蒂于知识共享,技术传承,更愿为讲师耕织嫁衣,助您成为PostgreSQL圈的意见领袖,用知识改变世界! 一.入选讲师 ...

  3. Java随想1

      1If(条件){输出} Else{ } 2Switch确定范围 定值 Switch(i1){ Case 值: 输出 Break 3Do while循环 定值 Do{ 输出 运算 }while(范围 ...

  4. MVC 与 Vue

    MVC 与 Vue 本文写于 2020 年 7 月 27 日 首先有个问题:Vue 是 MVC 还是 MVVM 框架? 维基百科告诉我们:MVVM 是 PM 的变种,而 PM 又是 MVC 的变种. ...

  5. mybatis 查询返回的类型中字段类型为 List<xx>

    基本类型数组 mapper.xml <resultMap id="xxDtoResultMap" type="com.xx.xxDto"> < ...

  6. 常见排序算法的golang 实现

    五种基础排序算法对比 五种基础排序算法对比 1:冒泡排序 算法描述 比较相邻的元素.如果第一个比第二个大,就交换它们两个: 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素 ...

  7. 535. Encode and Decode TinyURL - LeetCode

    Question 535. Encode and Decode TinyURL Solution 题目大意:实现长链接加密成短链接,短链接解密成长链接 思路:加密成短链接+key,将长链接按key保存 ...

  8. 关于vue.config.js 的 proxy 配置

    关于vue.config.js 的 proxy 配置有的同学不怎么明白项目里面有的配置了 pathRewrite 地址重写,有的又没有进行配置?/* * proxy代理配置的说明 * *接口例子:/z ...

  9. 做一个能对标阿里云的前端APM工具（下）

    上篇请访问这里做一个能对标阿里云的前端APM工具(上) 样本多样性问题 上一小节中的实施方案是微观的,即单次性的.具体的.但是从宏观上看,我需要保证性能测试是公允的,符合大众预期的.为了达到这种效果, ...

  10. OpenWrt 20.02.2 小米路由器3G配置CP1025网络打印

    家里的施乐 CP116w 工作快五年了终于罢工了. 黑粉报错, 自己也不会拆, 只能搁置了. 后来换了个 HP CP1025. 这个打印机也不错, 墨盒便宜没什么废粉, 就是启动慢一点, 而且 -- ...