22.1.23Manacher算法、双端队列、单调栈

22.1.23Manacher算法、双端队列、单调栈

1.Manacher算法

1）用途：

• Manacher算法用于解决类似求某个字符串中最长的回文子串。（回文就是正着读和倒着读一样的结构）。

2）算法中的关键变量：

• 回文半径 r：回文直径的一半；

• 回文直径 d：整个回文的长度；

• 之前扩大的所有位置中所到达的回文直径d的最右边界R；

• 中心点c：取得R的那个点；

• 回文半径数组:储存遍历字符串所得到的每个点的回文半径；

3）算法的流程：

• 伪代码：

• 

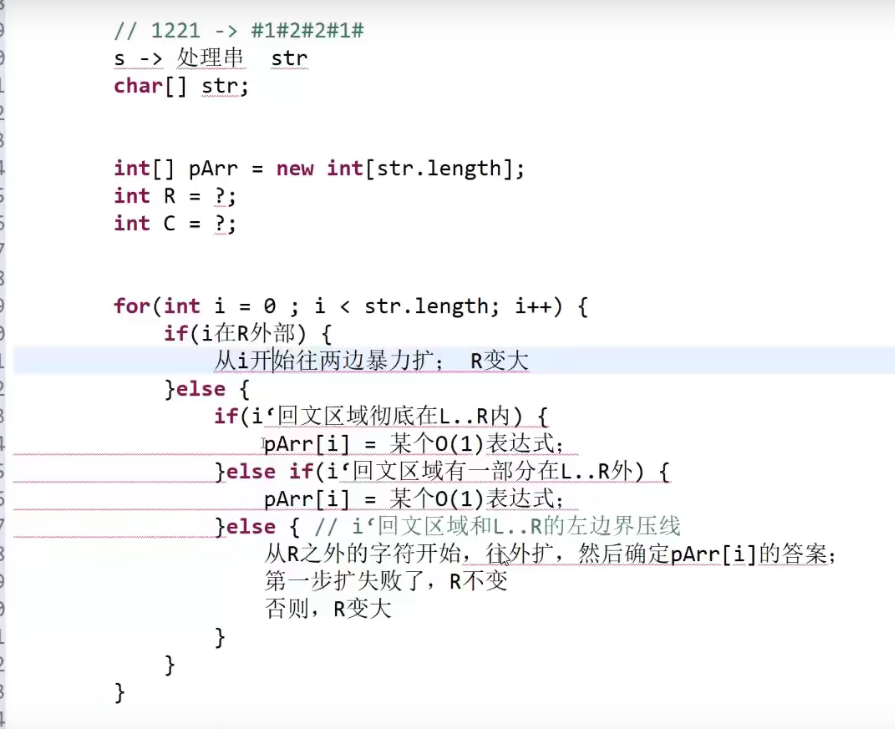
• 这里的R与上述提到的概念不太相同，这里是回文最右边界的下一位。对字符串依次遍历，我们回遇到三种情况：

  • 当前遍历到的元素不在回文的有边界R内：此时没什么优化的方法，直接暴力扩大，判断扩大的是否为回文结构。

  • 当前遍历到的元素在右边界内：此时可以做出如下的位置关系：（L是R关于中心c的对称点，i'是i（当前遍历的点）的对称点），此时i的回文直径，回文半径都与他的对称点i'相同（根据对称的性质即可证明）。

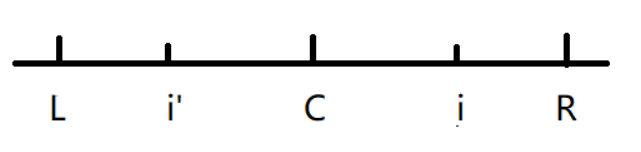
  • 当前遍历到的元素的对称点的回文直径的左边界在L的左边：如下图，此时i的回文半径就是i~R所表示的区域。下面给出证明：x，y分别为L，L'的前一个数和后一个数，k，z也同理。由c扩得的回文区域是L~R所表示的区域，那我们就知道x！=z的，根据i'的会问区域的左边界是超过了L的，我们能知道：至少是x，y也在i'的回文区域内，所以x=y的，y=k，因为x！=z的，所以k！=z。

  • 

  • 当前遍历到的元素的对称点的回文直径的左边界刚好与L重合：如下图：此时i的回文半径就是i'的回文半径。对称可证。

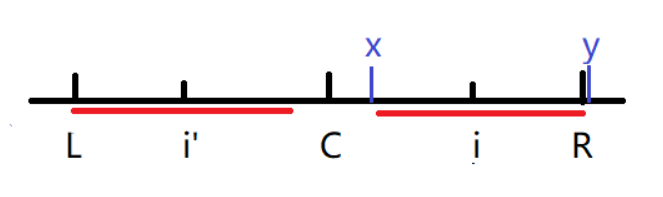
• code：

    public static char[] manacherString(String str) {
        char[] charArr = str.toCharArray();
        char[] res = new char[str.length() * 2 + 1];
        
        int index = 0;
        for (int i = 0; i != res.length; i++) {
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }
​
    public static int maxLcpsLength(String str) {
        if (str == null || str.length() == 0) {
            return 0;
        }
        char[] charArr = manacherString(str);
        int[] pArr = new int[charArr.length];
        int C = -1;
        int R = -1;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i != charArr.length; i++) {
            pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
            //
            while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
                    pArr[i]++;
                else {
                    break;
                }
            }
            if (i + pArr[i] > R) {
                R = i + pArr[i];
                C = i;
            }
            max = Math.max(max, pArr[i]);
        }
        return max - 1;
    }
​
    public static void main(String[] args) {
        String str1 = "abc1234321ab";
        System.out.println(maxLcpsLength(str1));
    }
​

2.双端队列

1）问题：

• 给定一个输入int[] arr, 窗口大小为w，输出长度为n-w+1得到数组res，res中包含每次窗口中的最大值。

2）思路（进阶：L，R自由移动的情况）：

• 设置一个双端队列，前后都可以进出，当R右移时，队列后面进入一个数组元素的下标（一直数组通过下标可以得到这个数），双端队列中始终要维持单调（如果是求窗口最大值则保持从大到小的结构，反之求最小值就保持从小到大的结构）。

  • 当L右移时，双端队列就从前边淘汰一个元素。L对应的队列中的元素始终是L~R范围上的最大值。

  • 在R移动时，如果遇到当前要进入队列的数大于已经进入队列的数，则弹出小于等于当前数的数，遇到大于当前数或队列为空时在让当前数进入；

  • 如果当前数小于队列中的最后一个属就直接进入。

3）code：

    public static int[] getMaxWindow(int[] arr, int w) {
        if (arr == null || w < 1 || arr.length < w) {
            return null;
        }
        LinkedList<Integer> qmax = new LinkedList<Integer>();
        int[] res = new int[arr.length - w + 1];
        int index = 0;
        for (int i = 0; i < arr.length; i++) {
            while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[i]) {
                qmax.pollLast();
            }
            qmax.addLast(i);
            if (qmax.peekFirst() == i - w) {
                qmax.pollFirst();
            }
            if (i >= w - 1) {
                res[index++] = arr[qmax.peekFirst()];
            }
        }
        return res;
    }
​
    // for test
    public static void printArray(int[] arr) {
        for (int i = 0; i != arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
​
    public static void main(String[] args) {
        int[] arr = { 4, 3, 5, 4, 3, 3, 6, 7 };
        int w = 3;
        printArray(getMaxWindow(arr, w));
​
    }

3.单调栈

1）问题：

• 求数组中任意一个数左右两边比他大（或小）且离他最近的两个数。

2）思路：

• 在无重复值的情况下，设置一个栈结构，若求大的情况则栈中从栈底到栈顶的顺序为从大到小，反之求两边小的数的情况顺序就为从小到大。下面以求解左右两边较大的数来讨论。

• 在一个数进站时，先判断栈是否为空或者当前的数是否小于栈顶的数，满足其中任意一种情况就直接压入栈，反之就从栈顶开始出栈，同时记录下出栈元素左边的距离他最近的且比它大的数是压在栈顶下面的数，右边的距离他最近的且比它大的数是即将入栈的数。重复操作直到栈为空或者遇到了比即将入栈的数大的数就停止操作，把即将入栈的数压入栈中。

• 当遍历完是数组的最后一个元素时，开始清栈操作。具体的做法为一次弹出栈顶元素，记录左边的距离栈顶元素最近的且比它大的数是压在栈顶下面的数，右边的为空，直到栈空。

3）code：

//待补充