树形dp专栏

前言

自己树形dp太菜了，要重点搞

219D Choosing Capital for Treeland

终于自己做了一道不算那么毒瘤的换根dp

令 \(f[u]\) 表示以 \(u\) 为根，子树内总共需要交换的边数， \(up[u]\) 表示以 \(u\) 为根，子树外总共需要交换的边数。

Dfs1 求出 \(f[u]\) ，就有：

\[f[u]=\sum_{v∈son[u]} f[v] + (edge[u->v] == 1)
\]

edge[u->v] 表示 u->v 这条边的方向是不是 u->v

Dfs2 求出 \(up[v]\)（注意，是从u点求u的儿子点v），容斥一下，就有：

\[up[v]=f[u]-f[v]+up[u]+(+1 / -1)
\]

(+1 / -1) 是看 edge[u->v]是否等于 1，是的话就有多一条边交换方向，不是的话就要-1，因为多算了一条边

Code

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int N = 2e5+7;
int n,cnt;
int head[N],f[N],up[N];
struct Edge {
	int next,to,flag;
}edge[N<<1];
inline void add(int u,int v,int flag) {
	edge[++cnt] = (Edge)<%head[u],v,flag%>;
	head[u] = cnt;
}
void Dfs1(int u,int fa) {
	for(int i=head[u];i;i=edge[i].next) {
		int v = edge[i].to;
		if(v != fa) {
			Dfs1(v,u);
			f[u] += f[v] + (edge[i].flag==0); //反边
		}
	}
}
void Dfs2(int u,int fa) {
	for(int i=head[u];i;i=edge[i].next) {
		int v = edge[i].to;
		if(v != fa) {
			up[v] = f[u] - f[v] + up[u];
			if(edge[i].flag == 1) up[v]++;
			else up[v]--;
			Dfs2(v,u);
		}
	}
}
int main()
{
	n = read();
	for(int i=1,u,v;i<=n-1;++i) {
		u = read(), v = read();
		add(u,v,1), add(v,u,0);
	}
	Dfs1(1,0);
	Dfs2(1,0);
	int ans = INF;
	for(int i=1;i<=n;++i)
		ans = min(ans,f[i]+up[i]);
	printf("%d\n",ans);
	for(int i=1;i<=n;++i)
		if(f[i]+up[i] == ans) printf("%d ",i);
	return 0;
}

533B Work Group

这题都看了题解才会（虽然说想到了题解这个状态，但不会转移）。。。dp功力还不行啊qwq

令 \(f[u][0/1]\) 表示子树总和为 偶数/奇数 的最大价值（且包括根，但是根可以选或不选）

有人也许会说，奇数怎么可呢，不是说一定要偶数吗？（其实这个自己推推数据在纸上画画就差不多知道了）

像下面这张图

黑色代表选了。不选根就可以选奇数的儿子呗。转移

\[f[u][0]=\max_{v∈son[u]}\{f[v][0]+f[u][0],f[v][1]+f[v][1]\}
\]

\[f[u][1]=\max_{v∈son[u]}\{f[v][0]+f[u][1],f[v][1]+f[u][0]\}
\]

最后 \(f[u][1]=\max\{f[u][1],f[u][0]+p[u]\}\)

（1代表奇，0代表偶）1+1=0,0+0=0; 1+0=0+1=1; 这个很好理解。

可是这个 \(f[u][0]\) 来更新 \(f[u][0]\) 怎么理解呢？

其实就是前面这个 \(f[u][0]\) 是我们待更新的，后面这个 \(f[u][0]\) 是之前遍历的子树里的总最优解，意义有所不同。遍历过程中的 \(f[u][0]\) 稍别与\(f[u][0]\)的定义的，只有所有更新结束后它才是u的子树选偶数个的最大值qwq。（这个不是很简单的东西吗，你怎么想了这么久啊，我确实想了这么久）

Code

#include<bits/stdc++.h>
#define INF 1e18
#define int long long
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int N = 2e5+7;
int n,cnt;
int head[N],p[N];
int f[N][2];	//f[i,0/1] 表示以i为根 子树总数是偶数/是奇数的
struct Edge {
	int next,to;
}edge[N<<1];
inline void add(int u,int v) {
	edge[++cnt] = (Edge)<%head[u],v%>;
	head[u] = cnt;
}
void Dfs1(int u,int fa) {
	//printf("QLL:: %d %d\n",u,fa);
	f[u][1] = -INF;	//f[u,1] 开始不能是奇数
	for(int i=head[u];i;i=edge[i].next) {
		int v = edge[i].to;
		if(v != fa) {
			Dfs1(v,u);
			int x0 = f[u][0], x1 = f[u][1];
			f[u][0] = max(f[u][0],max(x0+f[v][0],x1+f[v][1]));
			f[u][1] = max(f[u][1],max(x0+f[v][1],x1+f[v][0]));
		}
	}
	f[u][1] = max(f[u][1],f[u][0]+p[u]);
	//printf("ELL :: %d %d %d\n",u,f[u][0],f[u][1]);
}
signed main()
{
	n = read();
	for(int i=1,u;i<=n;++i) {
		u = read(); p[i] = read();
		if(u!=-1) add(u,i), add(i,u);
	}
	Dfs1(1,0);
	printf("%lld\n",max(f[1][0],f[1][1]));
	return 0;
}

700B Connecting Universities

挺思维的一题。从点与点的配对完全没有办法下手，从整体的考虑，一条边可以有几条路径经过，这题就迎刃而解了

假如一条边连的两个点 \((x,y)\) ，\(x\)这边这一团的大学有 \(f[x]\) 座，\(y\)这边的这一团大学有\(f[y]\)，我们一定要让 \(\min(f[x],f[y])\) 座大学经过这条边与另一端的大学配对。为什么？

令 \(f[x]<f[y]\) 如果 \(x\) 这边这\(f[x]\)个大学不去经过这条边 \((x,y)\) 向另一端配对，在 \(x\) 这边这一端自己给自己配对，答案就不是最优，自己给自己配对没有发展，最后：

\[ans=\sum\min(f[u],2*K-f[u])
\]

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int N = 200007;
int n,m,cnt,K,ans;
int head[N],f[N];
struct Edge {
	int next,from,to;
}edge[N<<1];
inline void add(int u,int v) {
	edge[++cnt] = (Edge)<%head[u],u,v%>;
	head[u] = cnt;
}
void Dfs(int u,int fa) {
	for(int i=head[u];i;i=edge[i].next) {
		int v = edge[i].to;
		if(v != fa) {
			Dfs(v,u); f[u] += f[v];
		}
	}
	ans += min(f[u],K-f[u]);
}
signed main()
{
	n = read(), K = read(); K <<= 1;
	for(int i=1,x;i<=K;++i)
		x = read(), f[x]++;
	for(int i=1,u,v;i<=n-1;++i) {
		u = read(), v = read();
		add(u,v), add(v,u);
	}
	Dfs(1,0);
	printf("%lld\n",ans);
	return 0;
}

Anton and Tree

又是一道思维难度很高的题。。。

作为提高组选手应该都能想到把一团相同颜色的点缩成一团。这个图就变成了黑白相间的一棵树。

首先这是样例里的树

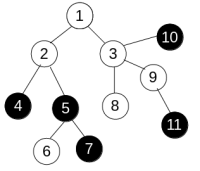
如我所说，把同色点缩成一个点就是这个样子

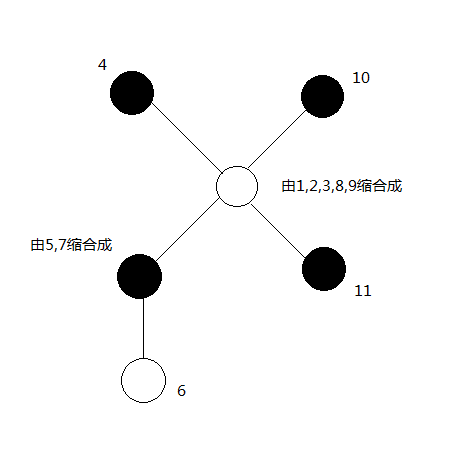
接下来就是推推结论了，（作为提高组选手应该会觉得很好推）

先给结论： 最少点击次数=(缩点后树的直径+1)/2。为什么呢？

我们不妨把直径拎出来，假设现在的直径就是下面这个图：

我们最优策略是对直径中间的一点点击一下，这样它周围的两个点就和他缩在一起了，就相当于这条链的长度-2，比如下面这张图;

因此对把直径单独拎出来最后缩成一个点的次数可以算出是 \(\frac{d+1}{2}\) （当然这里的直径d是指边数，结果向下取整）

为什么这棵树要操作的次数就是直径要操作的次数呢？

对此，我们可以把其他点看成直径上一些点的分支，如下图：

自己手推一下直径的缩点过程，发现缩点的同时，分支也缩了一些点进去，而且，缩了一圈。进而发现这些分支会先缩完，为什么？

每缩完一个点，这个点的周围就会缩小一圈，那树上最长的一条链是什么啊？直径呗。所以比直径小的会在缩直径的同时一起缩完（这样讲能理解吧，因为我很菜，不会严格的证明，再有问题就自己手推吧）

Code

#include<bits/stdc++.h>
using namespace std;
inline int read() {
	int x=0,f=1; char ch=getchar();
	while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
	return x * f;
}
const int N = 200007;
int n,m,cnt,mxc,ans;
int head[N];
bool col[N];
struct Edge {
	int next,to;
}edge[N<<1];
inline void add(int u,int v) {
	edge[++cnt] = (Edge)<%head[u],v%>;
	head[u] = cnt;
}
void Dfs(int u,int fa,int dep) {
	if(dep > ans) {
		mxc = u; ans = dep;
	}
	for(int i=head[u];i;i=edge[i].next) {
		int v = edge[i].to;
		if(v != fa) {
			if(col[u]==col[v]) Dfs(v,u,dep);
			else Dfs(v,u,dep+1);
		}
	}
}
int main()
{
	n = read();
	for(int i=1;i<=n;++i) col[i] = read();
	for(int i=1,u,v;i<=n-1;++i) {
		u = read(), v = read();
		add(u,v), add(v,u);
	}
	Dfs(1,0,0);
	Dfs(mxc,0,0);
	printf("%d\n",(ans+1)>>1);
	return 0;
}