cftool拟合&函数逼近

cftool拟合&函数逼近

cftool

真是神奇，之前我们搞的一些线性拟合解方程，多项式拟合，函数拟合求参数啊，等等。

已经超级多了，为啥还得搞一个cftool拟合啊？而且毫无数学理论。

如果你足够细心，你会发现，之前的拟合，都是我们猜测这个拟合的式子大概是什么形式，只需要求个参数。嘿嘿到底准不准呢？ 数据及其简单才会被你发现规律呢！

这里在cftool的帮助下不停的尝试才能得到最好的拟合形式。

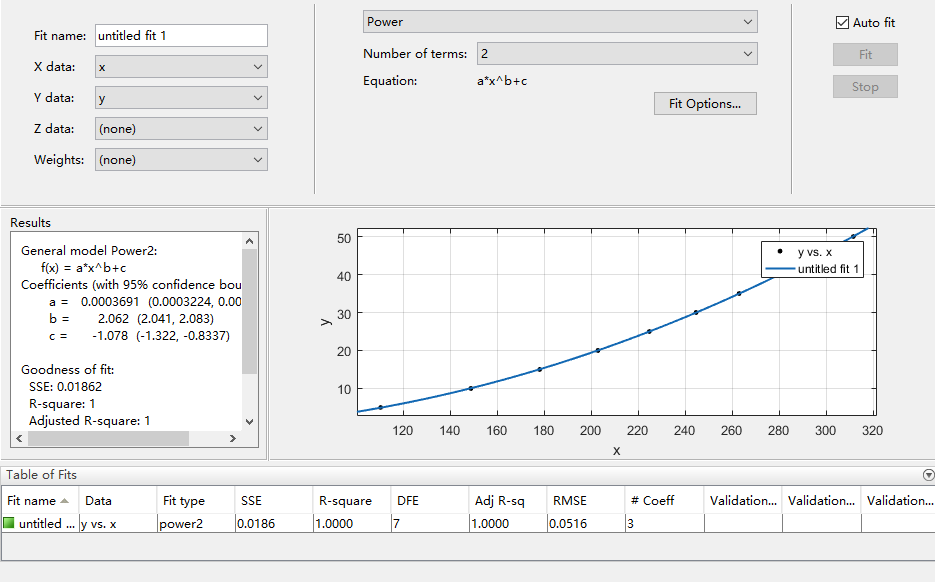
可以看出，拟合形式多样，拟合分析方便。

· Custom Equations：用户自定义的函数类型
· Exponential：指数逼近，有2种类型， a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x)
· Fourier：傅立叶逼近，有7种类型，基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)
· Gaussian：高斯逼近，有8种类型，基础型是 a1*exp(-((x-b1)/c1)^)
· Interpolant：插值逼近，有4种类型，linear、nearest neighbor、cubic spline、shape-preserving
· Polynomial：多形式逼近，有9种类型，linear ~、quadratic ~、cubic ~、-9th degree ~
· Power：幂逼近，有2种类型，a*x^b 、a*x^b + c
· Rational：有理数逼近，分子、分母共有的类型是linear ~、quadratic ~、cubic ~、-5th degree ~；此外，分子还包括constant型
· Smoothing Spline：平滑逼近（翻译的不大恰当，不好意思）
· Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是 a1*sin(b1*x + c1)
· Weibull：只有一种，a*b*x^(b-)*exp(-a*x^b)

函数逼近

给一个栗子吧：

​ 用 ​ 来拟合。

我们已经可以通过自己已经学的办法来解决这个问题了（四个函数都可以使用，大致两条思路）

方法一：首先生成数据，然后写矩阵

方法二：函数形式

（当然还有多项式拟合方法，和解方程法，没想到有不知不觉已经学了5个方法了）

x = -pi/:pi/:pi/;
y = cos(x);
x = x';
y = y';
r = [ones(,),x.^,x.^];
sx = lsqlin(r,y);

​

函数逼近答案：

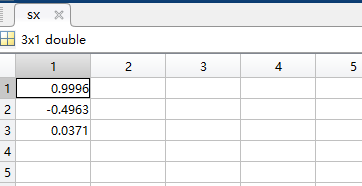
方法二：

x = -pi/:pi/:pi/;
y = cos(x);
F = @(sx)sx()+sx()*x.^+sx()*x.^-y;
cs0 = rand(,);
cs = lsqnonlin(F,cs0);

拟合效果也是杠杠的。

现在还有一个方法，哈哈，开心吧！

老实说，看上去有点像解方程，当然是班门弄斧了，里面的原理已经完全不一样了。

既然已经有函数了，还要麻烦的用这个函数去生成数据吗？

稍微看了一点理论，还是超级复杂的。哈哈，我等人才还得加油了。

看一下格式吧：

clc,clear;
syms x;
base = [,x^,x^];
y1 = base.'*base;
y2 = cos(x)*base.';
r1 = int(y1,-pi/,pi/);
r2 = int(y2,-pi/,pi/);
a = r1\r2;
xishu1 = double(a);
xishu2 = vpa(a,);

至此，第一个数学建模模型，插值和拟合，已经完成了。恭喜啦！！！