无环的visitor模式

　　无环的访问者模式，是来改进原有访问者模式的不足之处的，是Robert C. Martin首次提出的。我们知道访问者模式的优点是为被访问继承体系动态添加行为，而无须改变继承体系。但是GOF访问者模式的缺点是形成了一个循环依赖，强烈的耦合了两个继承体系，使得我们修改任何一方都会对另一方造成影响，所以GOF提出，被访问者的继承体系必须是稳定的，否则，一旦被访问的继承体系修改了，两边都要改。

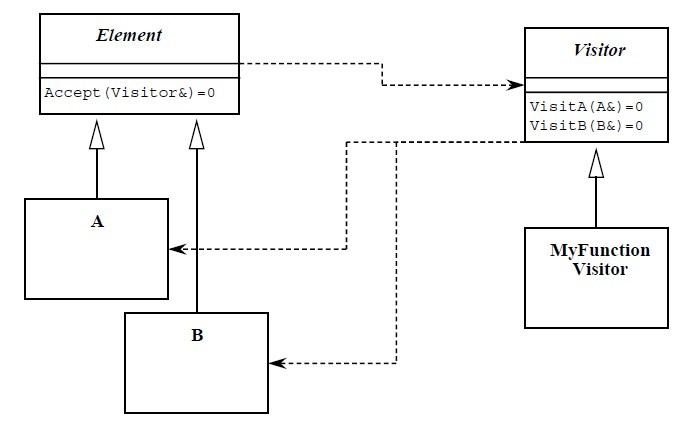
GOF访问者模式的UML类图。从图中可以看到循环依赖，一旦被访者体系发生变化，则访问者体系就要修改，这是难以接受的。

　　Robert C. Martin提出了一种无环的访问者模式来改进原有的不足，通过改进后，循环依赖被打破了，也不要求被访问层次必须是
稳定的，即使是被访问者继承层次修改了，也不需要修改访问者层次，只需要扩展一下即可，而且访问者可以自由组合较之以前更

为灵活方便。但是也是有代价的，有一个向下的转换，性能会稍有损失，但相对于改进的好处来说，这点损失几乎可以忽略了。

　　从上图我们可以看到，循环依赖被打破了，访问者基类不再依赖于被访问者的具体类型了，只是依赖于一个空的访问者基类，因此它是稳定的。通过多重继承，我们可以自由的组合访问者，比以前将访问函数放到一个类中更灵活。下面看看c++中具体的实现吧。

///////////////访问者基类
template<typename T>
struct Visitor
{
    virtual void Visit( T&) = ;
};

struct VistorToken
{
    virtual ~VistorToken(){}
};

/////////////////被访问者基类
struct Base
{
    virtual void Accept(VistorToken&) = ;
    virtual ~Base(){}
};

/////////////////具体的被访问者
struct AV;
typedef Visitor<AV> AVVisitor;

struct BV;
typedef Visitor<BV> BVVisitor;

struct AV : public Base
{
    double val;
    void Accept(VistorToken& v)
    {
        if (AVVisitor* ev = dynamic_cast<AVVisitor*>(&v))
            ev->Visit(*this);
    }
};

struct BV : public Base
{
    double val;
    void Accept(VistorToken& v)
    {
        if (BVVisitor* ev = dynamic_cast<BVVisitor*>(&v))
            ev->Visit(*this);
    }
};

////////////////////////具体的自定义访问者
struct CustomerVisitor : public VistorToken, public AVVisitor, public BVVisitor
{
    void Visit(AV& a)
    {
        std::cout << "from AV: " << a.val << std::endl;
    }
    void Visit(BV& b)
    {
        std::cout << "from BV: " << b.val << std::endl;
    }
};

测试程序：

void OtherVisitor()
{
    AV a; a.val = 10.1;
    BV b; b.val = 9.2;
    CustomerVisitor v;
    Base* b1 = &a;
    Base* b2 = &b;
    b1->Accept(v);
    b2->Accept(v);
}

　　不知道无环的访问者模式我讲清楚没有，可能有点难理解，没关系，自己动手实践一下，再回过头来看介绍也许就明白了怎么回事了。

　　c++11 boost技术交流群：296561497，欢迎大家来交流技术。