建模算法（九）——拟合

一、线性最小二乘法

1、基本思路

令，其r(x)是事先选定的一组线性无关的函数。ak是待定系数。然后拟合的准则就是使得yi与f(xi)的距离的平方和最小，称之为最小二乘准则

2、系数的确定

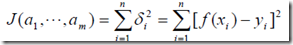，要使距离的平方和最小，那只要取得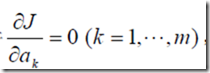，使得取到极值，就可以解除待定系数ak，记

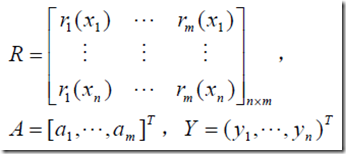
然后线性方程组为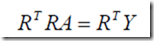，所以当R列满秩，R’R是可逆的，所以方程组有唯一解

3、函数r(x)的选取

一般是直观的去判断用什么样的曲线。然后下面有一般常用的曲线

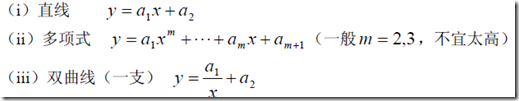
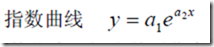一般需要做变量代换，化为对a1和a2的线性函数。

然后可以多选几个r（x），然后选择距离的平方和最小的一个。

4、MATLAB实现

（1）解方程法

一个demo

function ab=Zuixiaoerchengfa(x,y)
%x，y为数据点，但是要为行向量

x=x';y=y';
r=[ones(5,1),x.^2];
ab=r\y;
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'bo',x0,y0,'r');

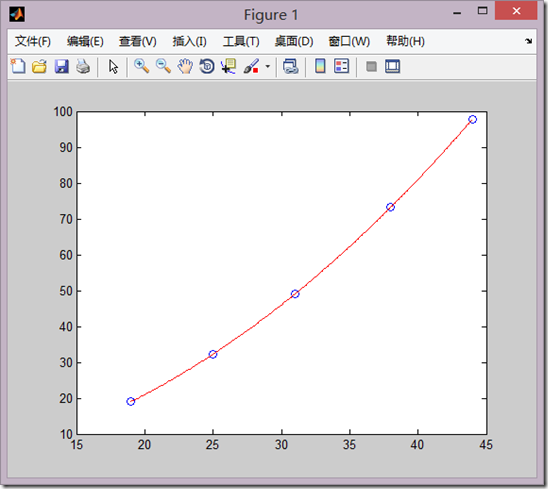
（2）多项式拟合法

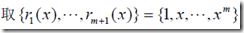，然后来拟合给定的数据，然后MATLAB由封装好的函数

a=ployfit(x0,y0,m)

多项式在x处的值y可以用这个函数计算

y=polyval(a,x)

其中x0，y0是要拟合的数据，m为拟合多项式的次数，输出参数a为拟合多项式的系数

一个demo

>> x0=[1990   1991   1992   1993   1994 1995  1996];
>> y0=[70  122 144  152   174  196  202];
>> plot(x0,y0,'*');

先画出散点图，观察使用多少次的多项式拟合

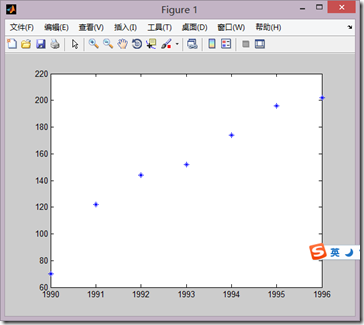
然后明显看出可以使用直线拟合所以

a=polyfit(x0,y0,1)

a =

   1.0e+04 *

    0.0021   -4.0705

>> y97=polyval(a,1997)

y97 =

  233.4286

>> y98=polyval(a,1998)

y98 =

  253.9286

>>

二、最小二乘优化

四、最重要的~~~~~~~~~~！！！！！！！！！！！！！！！！

曲线拟合的用户界面求法！！！！！！！！！！！！

直接使用命令cftool

五、曲线拟合与函数逼近

一个demo

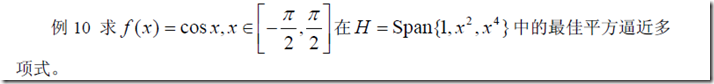
int用于符号∫

int(s)符号表达式s的不定积分.

int(s,v)符号表达式s关于变量v的不定积分.

int(s,a,b)符号表达式s的定积分, a,b分别为积分的下限和上限.

int(s,v,a,b)符号表达式s关于变量v从 a到b的定积分.

当int求不出符号解,会自动转求数值解.

syms x
base=[1,x^2,x^4];

y1=base.'*base
y2=cos(x)*base.'
r1=int(y1,-pi/2,pi/2)     %算积分
r2=int(y2,-pi/2,pi/2)

a=r1\r2
xishu1=double(a)
digits(8),xishu2=vpa(a)