71: libreoj #10151 区间dp

$des$

https://loj.ac/problem/10151

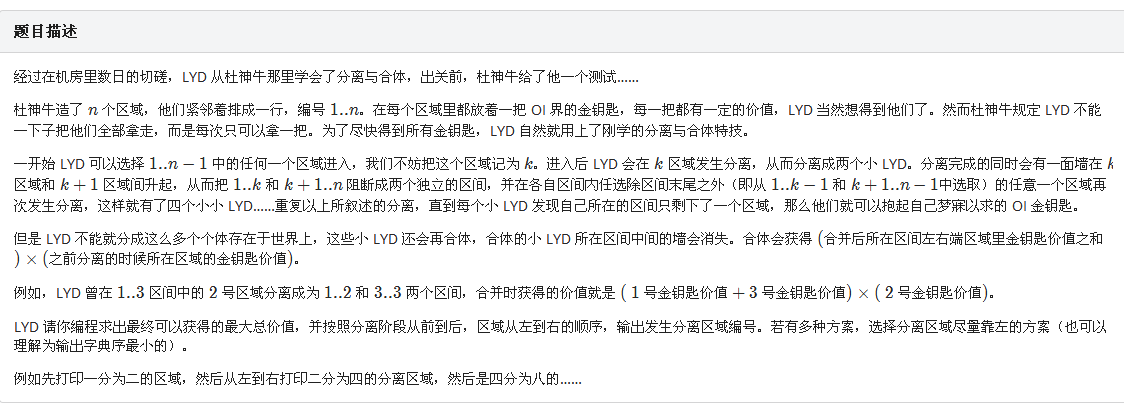
$sol$

区间dp

$f_{i, j}$ 表示区间 $[l, r]$ 合并的最大值

枚举中间点 $k$

$f_{i, j} =max(f_{i, j}, f_{i, k} + f_{k + 1, j} + (w_r + w_{l - 1}) \times w_k)$

对于方案的输出，$g_{i, j}$ 表示区间最优断点

bfs输出

#include <bits/stdc++.h>

const int N = ;

int f[N][N], g[N][N], w[N], n, sum[N];

int main() {
    std:: cin >> n;
    for(int i = ; i <= n; i ++) std:: cin >> w[i];
    for(int i = ; i <= n; i ++) sum[i] = sum[i - ] + w[i];
    for(int i = ; i <= n; i ++)
        for(int j = ; j <= n; j ++)
            f[i][j] = ( << );
    for(int i = ; i <= n; i ++) f[i][i] = ;
    for(int len = ; len <= n; len ++) {
        for(int l = ; l + len -  <= n; l ++) {
            int r = l + len - , add = -;
            for(int k = l; k < r; k ++) {
                int now = f[l][k] + f[k + ][r] + (w[r] + w[l]) * w[k];
                if(now > add) {
                    add = now, g[l][r] = k;
                }
            }
            f[l][r] = add;
        }
    }
    std:: cout << f[][n] << "\n";
    static int Answer[N], js = ;
    std:: queue < std:: pair<int, int> > Q;
    Q.push(std:: make_pair(, n));
    while(!Q.empty()) {
        std:: pair <int, int> tp = Q.front();
        Q.pop();
        Answer[++ js] = g[tp.first][tp.second];
        if(tp.first != g[tp.first][tp.second]) Q.push(std:: make_pair(tp.first, g[tp.first][tp.second]));
        if(tp.second != g[tp.first][tp.second] + ) Q.push(std:: make_pair(g[tp.first][tp.second] + , tp.second));
    }
    for(int i = ; i <= js; i ++) std:: cout << Answer[i] << " ";
    return ;
}