模拟赛 提米树 题解 （DP+思维）

题意：

有一棵棵提米树，满足这样的性质:

每个点上长了一定数量的Temmie 薄片，薄片数量记为这个点的权值，这些点被标记为 1 到 n 的整数，其

中 1 号点是树的根，没有孩子的点是树上的叶子。

定义\((a,b)\)是一对相邻的叶子，当且仅当没有其它的叶子节点在 DFS 序上在a,b 之间。

每对相邻的叶子都会产生一个代价，代价为 a 到 b 路径上(不包含 a,b)的点中，最大点权值。

提米树可以提供决心，一棵提米树能提供的决心的数量是树上所有叶子上长的 Temmie 薄片数量和，减去所有相邻叶子的代价。

Temmie 们决定对这棵树进行若干次剪枝(可以不剪枝)，使得这棵树能提供的决心最多。

一次剪枝定义为:如果一个点的孩子都是叶子,就可以把它所有的孩子剪掉。

要求\(O(n)\)做法。

首先，考虑\(O(n^2)\)的60分暴力：

我们可以反过来：由根开始，每个节点考虑是否扩展出所有叶子。

若不扩展，则它的子树都是空的，它成为叶子。

我们可以在dfs序上DP：设\(dp(i,j)\)表示考虑到i，上一个叶子点为j的最大决心。

有两种转移：

1、若i不是叶子，可以扩展，转移到\(dp(i+1,j)\)。

2、可以不扩展，转移到\(dp(i+si_i,i)+w_i-max(i,j)\)。

代码如下：

for(int i=tm-1;i>=0;i--)
{
	for(int j=0;j<=n;j++)
	{
		int u=xl[i];
		dp[i][j]=dp[i+si[u]][u]+sz[u]-zd[j][u];
		if(si[u]>1&&dp[i+1][j]>dp[i][j])
			dp[i][j]=dp[i+1][j];
	}
}
printf("%d",dp[0][0]);

考虑优化：首先，要把维度降下来。

设\(dp(i)\)表示i成为叶子后的最大决心。

枚举下一个使用2转移的位置，代码如下：

for(int i=tm;i>=0;i--)
{
	int u=xl[i];
	dp[i]=-999999999;
	for(int j=i+si[u];j<=tm+1;j++)
	{
		int t=dp[j]-zd[u][xl[j]];
		if(t>=dp[i])
			dp[i]=t;
		if(si[xl[j]]==1)//注意此处，非常关键。
			break;
	}
	dp[i]+=sz[u];
}
printf("%d",dp[0]);

继续优化：

我们发现，对于\(i\)，\(i+si_i\)就是i的祖先节点中第一个有更右子节点的点。

而由于注释处的break，使得转移就是在\(i+si[u]\)处，一直向左走形成的链。

那么：

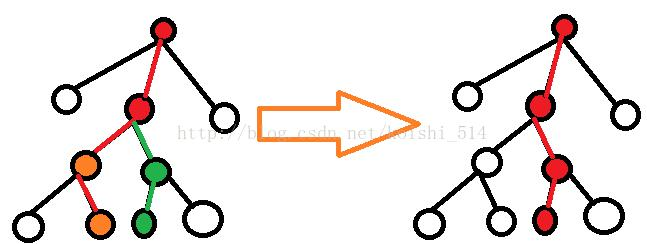
绿点对橙点有贡献。

那么，我们枚举红点lca，再枚举相邻的两个儿子，计算贡献。

先算出链上每个节点到lca的最大值。设为\(h\)，那么，就是\(dp(u)=max(dp(v)-max(h(u),h(v)))+w(u)\)。

由于h具有单调性，因此分\(h(u)>h(v)\)和\(h(u)<=h(v)\)进行讨论，提前算出链上\(dp\)，以及\(dp-h\)的最大值。

这两种情况符合的v一定是前缀/后缀，双指针扫一下即可定位。

代码细节非常多。

#include <stdio.h>
#include <vector>
#define inf 999999999
using namespace std;
vector<int> ve[100010];
int sz[100010],cl[100010],cr[100010],dp[100010],zd[100010],fa[100010],ma[100010],md[100010];
int max(int a,int b)
{
	return a>b?a:b;
}
void dfs0(int u,int f)
{
	fa[u]=f;
	for(int i=0;i<ve[u].size();i++)
		dfs0(ve[u][i],u);
}
void dfs1(int u)
{
	for(int i=ve[u].size()-2;i>=0;i--)
	{
		dfs1(ve[u][i+1]);
		int t=ve[u][i],la=0;zd[u]=sz[u];
		while(t!=0)
		{
			zd[t]=max(sz[t],zd[fa[t]]);
			t=cr[t];
		}
		t=ve[u][i+1];
		while(t!=0)
		{
			zd[t]=max(sz[t],zd[fa[t]]);
			la=t;t=cl[t];
		}
		t=la;while(t!=u)
		{
			ma[t]=dp[t]-zd[fa[t]];
			if(cl[t])ma[t]=max(ma[t],ma[cl[t]]);
			t=fa[t];
		}
		t=ve[u][i+1];
		while(t!=0)
		{
			md[t]=dp[t];
			if(fa[t]!=u)md[t]=max(md[t],md[fa[t]]);
			t=cl[t];
		}
		ma[u]=md[u]=-inf;
		int x=ve[u][i],y=ve[u][i+1];
		while(x!=0)
		{
			while(y!=0&&zd[fa[y]]<zd[fa[x]])
				y=cl[y];
			if(y)
			{
				t=ma[y]+sz[x];
				if(t>dp[x])dp[x]=t;
			}
			t=md[(y==0?la:fa[y])]-zd[fa[x]]+sz[x];
			if(t>dp[x])dp[x]=t;x=cr[x];
		}
	}
	if(ve[u].size())dfs1(cl[u]);
}
int main()
{
	freopen("temmie.in","r",stdin);
	freopen("temmie.out","w",stdout);
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int s,a;
		scanf("%d%d",&sz[i],&s);
		for(int j=0;j<s;j++)
		{
			scanf("%d",&a);
			ve[i].push_back(a);
		}
		if(s>0)
		{
			cl[i]=ve[i][0];
			cr[i]=ve[i][s-1];
		}
		dp[i]=-inf;
	}
	int u=1;
	while(u!=0)
	{
		dp[u]=sz[u];
		u=cr[u];
	}
	dfs0(1,0);dfs1(1);
	int ma=-inf;u=1;
	while(u!=0)
	{
		if(dp[u]>ma)
			ma=dp[u];
		u=cl[u];
	}
	printf("%d",ma);
	return 0;
}