三维网格细分算法（Catmull-Clark subdivision & Loop subdivision）附源码(转载)

转载：  https://www.cnblogs.com/shushen/p/5251070.html

下图描述了细分的基本思想，每次细分都是在每条边上插入一个新的顶点，可以看到随着细分次数的增加，折线逐渐变成一条光滑的曲线。曲面细分需要有几何规则和拓扑规则，几何规则用于计算新顶点的位置，拓扑规则用于确定新顶点的连接关系。下面介绍两种网格细分方法：Catmull-Clark细分和Loop细分。

Catmull-Clark subdivision：

　　Catmull-Clark细分是一种四边形网格的细分法则，每个面计算生成一个新的顶点，每条边计算生成一个新的顶点，同时每个原始顶点更新位置。下图为Catmull-Clark细分格式的细分掩膜，对于新增加的顶点位置以及原始顶点位置更新规则如下：

1.网格内部F-顶点位置：

　　设四边形的四个顶点为v₀、v₁、v₂、v₃，则新增加的顶点位置为v = 1/4*(v₀ + v₁ + v₂ + v₃)。

2.网格内部V-顶点位置：

　　设内部顶点v₀的相邻点为v₁、v₂，…，v_2n，则该顶点更新后位置为，其中α、β、γ分别为α = 1 - β - γ。

3.网格边界V-顶点位置：

　　设边界顶点v₀的两个相邻点为v₁、v₂，则该顶点更新后位置为v = 3/4*v₀ + 1/8*(v₁ + v₂)。

4.网格内部E-顶点位置：

　　设内部边的两个端点为v₀、v₁，与该边相邻的两个四边形顶点分别为v₀、v₁、v₂、v₃和v₀、v₁、v₄、v₅，则新增加的顶点位置为v = 1/4*(v₀ + v₁ + v_f¹ + v_f²) = 3/8*(v₀ + v₁) + 1/16*(v₂ + v₃ + v₄ + v₅)。

5.网格边界E-顶点位置：

　　设边界边的两个端点为v₀、v₁，则新增加的顶点位置为v = 1/2*(v₀ + v₁)。

效果：

function [VV, FF, S] = CC_subdivision(V, F, iter)
    % Catmull_Clark subdivision
    if ~exist('iter','var')
        iter = 1;
    end
    VV = V;
    FF = F;

    for i = 1:iter
        nv = size(VV,1);
        nf = size(FF,1);

        O = outline(FF);

        original = 1:nv;
        boundary = O(:,1)';
        interior = original(~ismember(original, boundary));

        no = length(original);
        nb = length(boundary);
        ni = length(interior);

        %% Sv
        Etmp = sort([FF(:,1) FF(:,2);FF(:,2) FF(:,3);FF(:,3) FF(:,4);FF(:,4) FF(:,1)],2);
        [E, ~, idx] = unique(Etmp, 'rows');

        Aeven = sparse([E(:,1) E(:,2)], [E(:,2) E(:,1)], 1, no, no);
        Aodd = sparse([FF(:,1) FF(:,2)], [FF(:,3) FF(:,4)], 1, no, no);
        Aodd = Aodd + Aodd';

        val_even = sum(Aeven,2);
        beta = 3./(2*val_even);

        val_odd = sum(Aodd,2);
        gamma = 1./(4*val_odd);

        alpha = 1 - beta - gamma;

        Sv = sparse(no,no);
        Sv(interior,:) = ...
            sparse(1:ni, interior, alpha(interior), ni, no) + ...
            bsxfun(@times, Aeven(interior,:), beta(interior)./val_even(interior)) + ...
            bsxfun(@times, Aodd(interior,:), gamma(interior)./val_odd(interior));
        Sboundary = ...
            sparse([O(:,1);O(:,2)],[O(:,2);O(:,1)],1/8,no,no) + ...
            sparse([O(:,1);O(:,2)],[O(:,1);O(:,2)],3/8,no,no);
        Sv(boundary,:) = Sboundary(boundary,:);

        %% Sf
        Sf = 1/4 .* sparse(repmat((1:nf)',1 ,4), FF, 1);
        i0 = no + (1:nf)';

        %% Se
        flaps = sparse([idx;idx], ...
                       [FF(:,3) FF(:,4);FF(:,4) FF(:,1);FF(:,1) FF(:,2);FF(:,2) FF(:,3)], ...
                       1);
        onboundary = (sum(flaps,2) == 2);
        flaps(onboundary,:) = 0;

        ne = size(E,1);
        Se = sparse( ...
                [1:ne 1:ne]', ...
                [E(:,1); E(:,2)], ...
                [onboundary;onboundary].*1/2 + ~[onboundary;onboundary].*3/8, ...
                ne, ...
                no) + ...
                flaps*1/16;

        %% new faces & new vertices
        i1 = no +   nf + (1:nf)';
        i2 = no + 2*nf + (1:nf)';
        i3 = no + 3*nf + (1:nf)';
        i4 = no + 4*nf + (1:nf)';

        FFtmp = [i0 i4 FF(:,1) i1; ...
                 i0 i1 FF(:,2) i2; ...
                 i0 i2 FF(:,3) i3; ...
                 i0 i3 FF(:,4) i4];

        reidx = [(1:no)'; no+(1:nf)'; no+nf+idx];
        FF = reidx(FFtmp);

        S = [Sv; Sf; Se];
        VV = S*VV;
    end
 end

Loop subdivision：

　　Loop细分是一种三角形网格的细分法则，它按照1-4三角形分裂，每条边计算生成一个新的顶点，同时每个原始顶点更新位置。下图为Loop细分格式的细分掩膜，对于新增加的顶点位置以及原始顶点位置更新规则如下：

1.网格内部V-顶点位置：

　　设内部顶点v₀的相邻点为v₁、v₂，…，v_n，则该顶点更新后位置为，其中。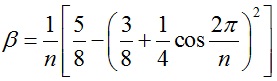

2.网格边界V-顶点位置：

　　设边界顶点v₀的两个相邻点为v₁、v₂，则该顶点更新后位置为v = 3/4*v₀ + 1/8*(v₁ + v₂)。

3.网格内部E-顶点位置：

　　设内部边的两个端点为v₀、v₁，相对的两个顶点为v₂、v₃，则新增加的顶点位置为v = 3/8*(v₀ + v₁) + 1/8*(v₂ + v₃)。

4.网格边界E-顶点位置：

　　设边界边的两个端点为v₀、v₁，则新增加的顶点位置为v = 1/2*(v₀ + v₁)。

效果：