Python连载38-协程、可迭代、迭代器、生产者消费者模型

一、生产者消费者模型

import multiprocessing

from time import ctime

def consumer(input_q):

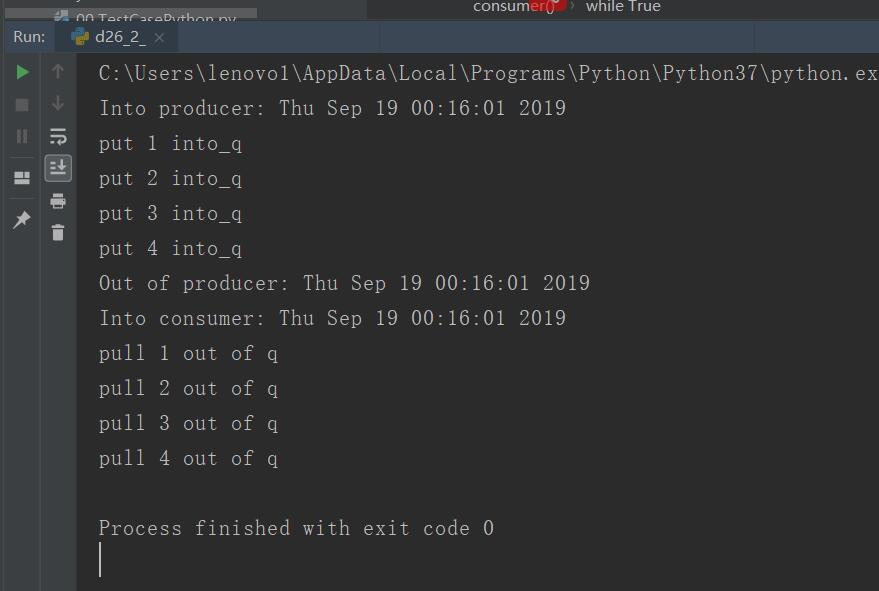
    print("Into consumer:",ctime())

    while True:

        #处理项

        item = input_q.get()

        print("pull",item,"out of q")#此处替换为有用的工作

        input_q.task_done()#发出信号通知任务完成

    print("Out of consumer:",ctime()) #此句未执行，因为q.join()收集到四个task_done()信号后，主进程启动

def producer(sequence,output_q):

    print("Into producer:",ctime())

    for item in sequence:

        output_q.put(item)

        print("put",item,"into_q")

    print("Out of producer:",ctime())

#建立进程

if __name__ == "__main__":

    q=multiprocessing.JoinableQueue()

    #运行消费者进程

    cons_p = multiprocessing.Process(target=consumer,args=(q,))

    cons_p.daemon = True

    cons_p.start()

​

    #生产多个项，sequence代表要发送给消费者的项序列

    #在实践中，这可能是生成器的输出或通过一些其他方式生产出来的

    sequence = [1,2,3,4]

    producer(sequence,q)

    #等待所有项被处理

    q.join()

二、协程

1.协程参考资料：

http://python.jobble.com/86481/

http://python.jobble.com/87310/

https://segmentfault.com/a/1190000009781688

2.迭代器参考资料

可迭代（iterable):直接作用于for循环变量

迭代器（Iterator):不但可以作用于for循环，还可以被next调用

3.关系：list是一个典型的可迭代对象，但是不是一个迭代器，因为list不可以被next调用

4.判断标准：通过isinstance来判断某个变量是否是一个实例，判断是否可以迭代

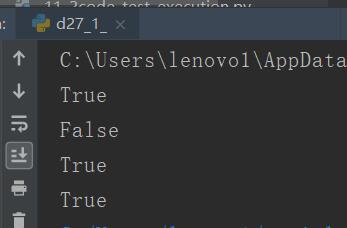
from collections import Iterable,Iterator

​

l = [i for i in range(5)]  #可迭代

print(isinstance(l,Iterable))#判断是否可迭代

print(isinstance(l,Iterator))#判断是否是一个迭代器

​

s_iter = iter(l)#将其转换为可以迭代的和迭代器

print(isinstance(s_iter,Iterable))#判断是否可迭代

print(isinstance(s_iter,Iterator))#判断是否是一个迭代器

三、源码

d26_2_consumer_and_producer_model.py

d27_1_iterable_and_iterator_and_their_transform.py

https://github.com/ruigege66/Python_learning/blob/master/d26_2_consumer_and_producer_model.py

https://github.com/ruigege66/Python_learning/blob/master/d27_1_iterable_and_iterator_and_their_transform.py​

2.CSDN：https://blog.csdn.net/weixin_44630050（心悦君兮君不知-睿）

3.博客园：https://www.cnblogs.com/ruigege0000/

4.欢迎关注微信公众号：傅里叶变换，个人公众号，仅用于学习交流，后台回复”礼包“，获取大数据学习资料