李航《统计学习方法》CH02

CH02 感知机

前言

章节目录

1. 感知机模型
2. 感知机学习策略
   1. 数据集的线性可分性
   2. 感知机学习策略
   3. 感知机学习算法
3. 感知机学习算法
   1. 感知机学习算法的原始形式
   2. 算法的收敛性
   3. 感知机学习算法的对偶形式

导读

感知机是二类分类的线性分类模型。

• $L(w,b)$的经验风险最小化
• 本章中涉及到向量内积，有超平面的概念，也有线性可分数据集的说明，在策略部分有说明损关于失函数的选择的考虑，可以和CH07一起看。
• 本章涉及的两个例子，思考一下为什么$\eta=1$，进而思考一下参数空间，这两个例子设计了相应的测试案例实现， 在后面的内容中也有展示。
• 在收敛性证明那部分提到了偏置合并到权值向量的技巧，这点在LR和SVM中都有应用。
• 第一次涉及Gram Matrix $G=[x_i\cdot x_j]_{N\times N}$
• 感知机的激活函数是符号函数.
• 感知机是神经网络和支持向量机的基础.
• 当我们讨论决策边界的时候, 实际上是在考虑算法的几何解释.
• 关于感知机为什么不能处理异或问题, 可以借助下图理解.

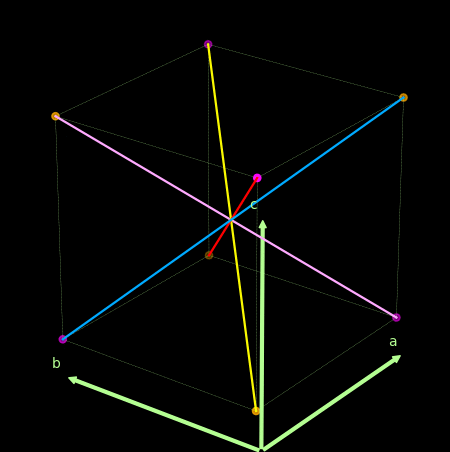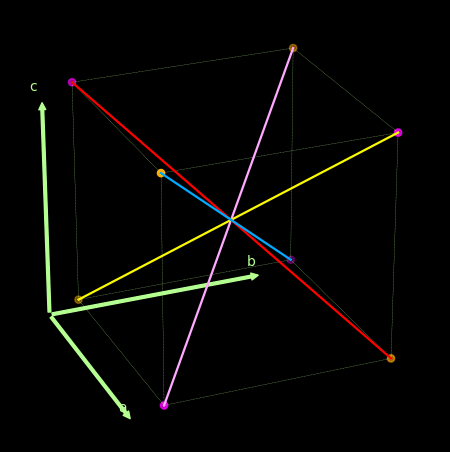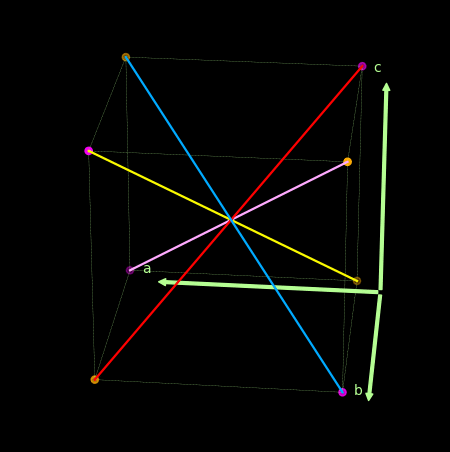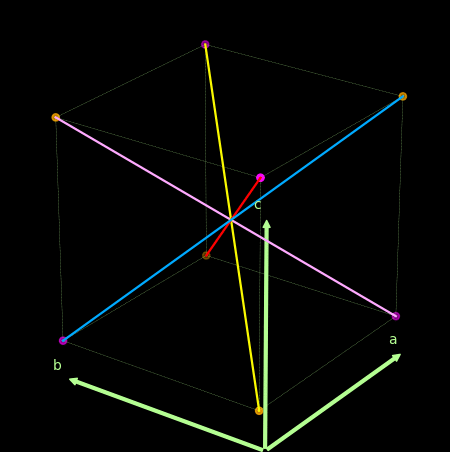
上面紫色和橙色为两类点, 线性的分割超平面应该要垂直于那些红粉和紫色的线.

三要素

模型

输入空间：$\mathcal X \subseteq \bf R^n$

输出空间：$\mathcal Y= {+1,-1} $

决策函数：$f(x)=sign (w\cdot x+b)$

策略

确定学习策略就是定义**(经验)**损失函数并将损失函数最小化。

注意这里提到了经验，所以学习是base在训练数据集上的操作

损失函数选择

损失函数的一个自然选择是误分类点的总数，但是，这样的损失函数不是参数$w,b$的连续可导函数，不易优化

损失函数的另一个选择是误分类点到超平面$S$的总距离，这是感知机所采用的

感知机学习的经验风险函数(损失函数)定义为误分类点到超平面S的总距离 $$ L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b) $$ 其中$M$是误分类点的集合

给定训练数据集$T$，损失函数$L(w,b)$是$w$和$b$的连续可导函数.

算法

原始形式

输入：$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}\ x_i\in \cal X=\bf R^n\mit , y_i\in \cal Y ={-1,+1}, i=1,2,\dots,N; 0<\eta\leqslant 1$

输出：$w,b;f(x)=sign(w\cdot x+b)$

1. 选取初值$w_0,b_0$

2. 训练集中选取数据$(x_i,y_i)$

3. 如果$y_i(w\cdot x_i+b)\leqslant 0$ $$ w\leftarrow w+\eta y_ix_i  \\ b\leftarrow b+\eta y_i $$

4. 转至(2)，直至训练集中没有误分类点

注意这个原始形式中的迭代公式，可以对$x$补1，将$w$和$b$合并在一起.

对偶形式

输入：$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}\ x_i\in \cal X=\bf R^n\mit , y_i\in \cal Y ={-1,+1}, i=1,2,\dots,N; \ \ 0<\eta\leqslant 1$

输出： $$ \alpha ,b; f(x)=sign\left(\sum_{j=1}^N\alpha_jy_jx_j\cdot x+b\right)\nonumber\ \alpha=(\alpha_1,\alpha_2,\cdots,\alpha_N)^T $$

1. $\alpha \leftarrow 0,b\leftarrow 0$

2. 训练集中选取数据$(x_i,y_i)$

3. 如果$y_i\left(\sum_{j=1}^N\alpha_jy_jx_j\cdot x+b\right) \leqslant 0​$ $$ \alpha_i\leftarrow \alpha_i+\eta \nonumber\ \\ b\leftarrow b+\eta y_i $$

4. 转至(2)，直至训练集中没有误分类点

Gram matrix

对偶形式中，训练实例仅以内积的形式出现。

为了方便可预先将训练集中的实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵 $$ G=[x_i\cdot x_j]_{N\times N} \nonumber $$

例子

例2.1

这个例子里面$\eta = 1$

感知机学习算法由于采用不同的初值或选取不同的误分类点，解可以不同。

另外，在这个例子之后，证明算法收敛性的部分，有一段为了便于叙述与推导的描述，提到了将偏置并入权重向量的方法，这个在涉及到内积计算的时候可能都可以用到，可以扩展阅读CH06，CH07部分的内容描述。

例2.2

这个例子也简单，注意两点

1. $\eta=1$
2. $\alpha_i\leftarrow \alpha_i+1, b\leftarrow b+y_i$

以上：

1. 为什么$\eta$选了1，这样得到的值数量级是1
2. 这个表达式中用到了上面的$\eta=1$这个结果，已经做了简化

所以，这里可以体会下，调整学习率$\eta $的作用。学习率决定了参数空间。

Logic_01

经常被举例子的异或问题^1，用感知机不能实现，因为对应的数据非线性可分。但是可以用感知机实现其他逻辑运算，也就是提供对应的逻辑运算的数据，然后学习模型。

这个例子的数据是二元的，其中NOT运算只针对输入向量的第一个维度

Logic_02

这个例子的数据是三元的.

MNIST_01

这个选择两类数据进行区分，不同的选择应该得到的结果会有一定差异，数据不上传了，在sklearn里面有相应的数据，直接引用了，注意测试案例里面用的是01，相对来讲好区分一些。