场景题：假设有40亿QQ号，但只有1G内存，如何实现去重？

当数据量比较大时，使用常规的方式来判重就不行了。例如，使用 MySQL 数据库判重，或使用 List.contains() 或 Set.contains() 判重就不行了，因为数据量太大会导致内存放不下，或查询速度太慢等问题。

1.空间占用量预测

正常情况下，如果将 40 亿 QQ 号存储在 Java 中的 int 类型的话，一个 int 占 4 字节（byte）那么 40 亿占用空间大小为：

4000000000*4/1024/1024/1024=14.9 GB

1GB=1024MB，1MB=1024KB，1KB=1024B（byte）

所以，我们无法使用正常的手段进行 40 亿 QQ 号的存储和去重判断，那怎么实现呢？

2.解决方案

此问题的常见解决方案有两种：

使用位数组 BitMap 实现判重。
使用布隆过滤器实现判重。

具体来说。

2.1 位数组实现判重

位数组是指使用位（bit）组成的数组，每个 QQ 号使用 1 位（bit）来存储，如下图所示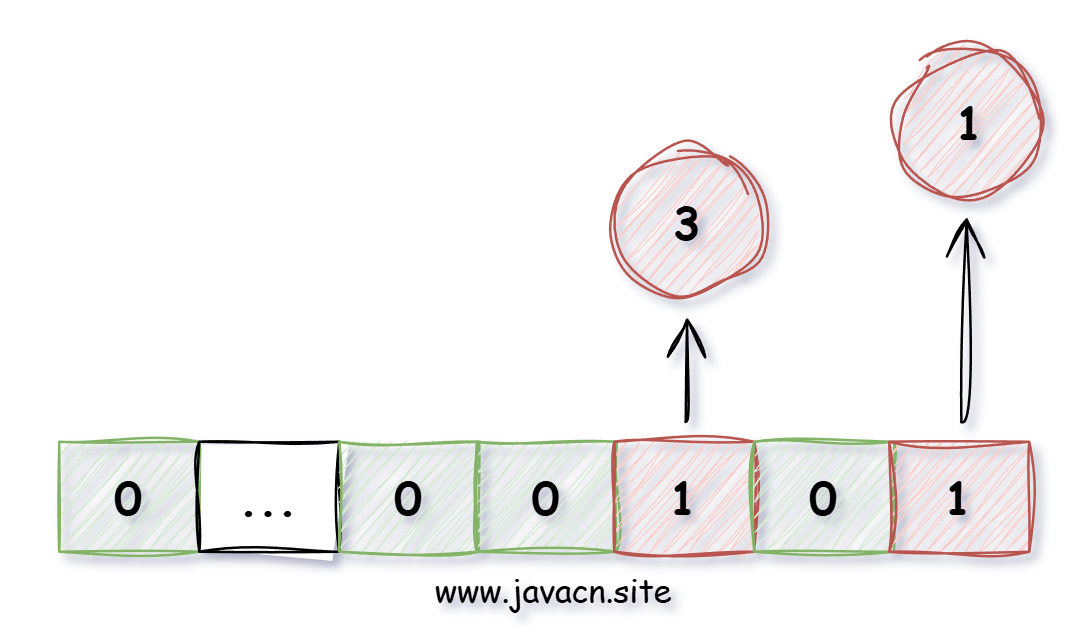：其中下标用来标识具体的数字，例如以上图片标识 1、3 数字存在，如果值为 0 表示不存在，这样的话 40 亿占用的位数组空间位 40 亿 bit，也就是 4000000000/1024/1024/1024/8=0.465 GB，不到 1G 的内存就可以存储 40 亿 QQ 号了，查询某个 QQ 号是否在线，只需要看这个 QQ 下标对应的位置是否为 1，1 表示存在，0 表示不存在。

位数组代码实现

位数组可以使用 Java 自带的 BitSet 来实现，它位于 java.util 包中，具体实现代码如下：

import java.util.BitSet;

public class BitmapExample {

    public static void main(String[] args) {

        // 创建一个BitSet实例

        BitSet bitmap = new BitSet();

        // 设置第5个位置为1，表示第5个元素存在

        bitmap.set(5);

        // 检查第5个位置是否已设置

        boolean exists = bitmap.get(5);

        System.out.println("Element exists: " + exists);  // 输出: Element exists: true

        // 设置从索引10到20的所有位置为1

        bitmap.set(10, 21);  // 参数是包含起始点和不包含终点的区间

        // 计算bitset中所有值为1的位的数量，相当于计算设置了的元素个数

        int count = bitmap.cardinality();

        System.out.println("Number of set bits: " + count);

        // 清除第5个位置

        bitmap.clear(5);

        // 判断位图是否为空

        boolean isEmpty = bitmap.isEmpty();

        System.out.println("Is the bitset empty? " + isEmpty);

    }

}

2.2 布隆过器实现

布隆过滤器是基于位数组实现的，它是一种高效的数据结构，由布隆在 1970 年提出。它主要用于判断一个元素可能是否存在于集合中，其核心特性包括高效的插入和查询操作，但存在一定的假阳性（False Positives）可能性。

布隆过滤器实现如下图所示：

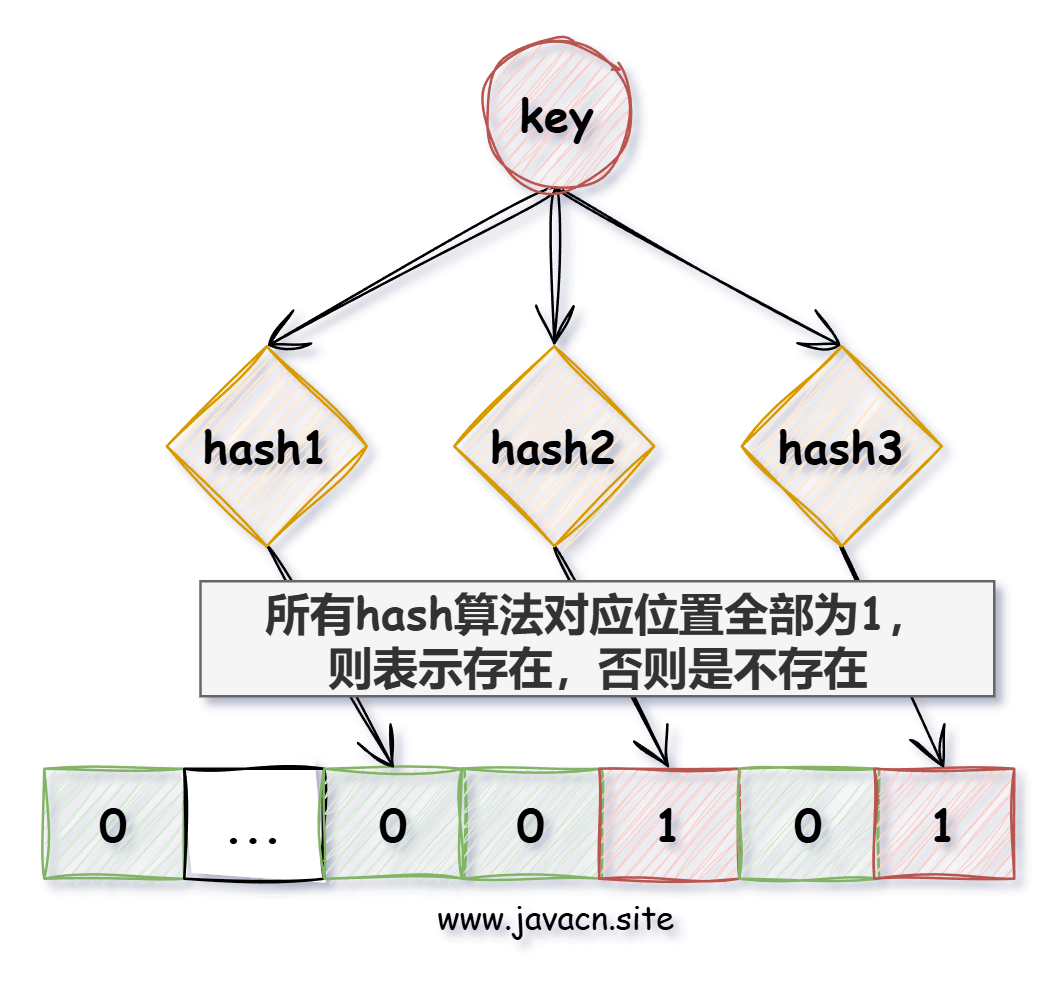
根据 key 值计算出它的存储位置，然后将此位置标识全部标识为 1（未存放数据的位置全部为 0），查询时也是查询对应的位置是否全部为 1，如果全部为 1，则说明数据是可能存在的，否则一定不存在。

布隆过器特性：如果布隆过滤器说一个元素不在集合中，那么它一定不在这个集合中；但如果它说一个元素在集合中，则有可能是不存在的（存在误差，假阳性）。

布隆过器代码实现

布隆过滤器的常见实现有以下几种方式：

使用 Google Guava BloomFilter 实现布隆过滤器，具体实现代码如下：

import com.google.common.hash.BloomFilter;

import com.google.common.hash.Funnels;

public class BloomFilterExample {

    public static void main(String[] args) {

        // 创建一个布隆过滤器，设置期望插入的数据量为10000，期望的误判率为0.01

        BloomFilter<String> bloomFilter =

        BloomFilter.create(Funnels.unencodedCharsFunnel(), 10000, 0.01);

        // 向布隆过滤器中插入数据

        bloomFilter.put("data1");

        bloomFilter.put("data2");

        bloomFilter.put("data3");

        // 查询元素是否存在于布隆过滤器中

        System.out.println(bloomFilter.mightContain("data1")); // true

        System.out.println(bloomFilter.mightContain("data4")); // false

    }

}

使用 Hutool 框架 BitMapBloomFilter 实现布隆过滤器，如下代码所示：

// 初始化

BitMapBloomFilter filter = new BitMapBloomFilter(10);

// 存放数据

filter.add("123");

filter.add("abc");

filter.add("ddd");

// 查找

filter.contains("abc");

使用 Redisson 框架中的 RBloomFilter 实现布隆过滤器，如下代码所示：

Config config = new Config();

config.useSingleServer().setAddress("redis://127.0.0.1:6379");

RedissonClient redissonClient = Redisson.create(config);

// 创建布隆过滤器，设置名称和期望容量与误报率

RBloomFilter<String> bloomFilter =

redissonClient.getBloomFilter("myBloomFilter");

bloomFilter.tryInit(10000, 0.03); // 期望容量 10000，误报率 3%

// 添加元素到布隆过滤器

String element1 = "element1";

bloomFilter.add(element1);

// 判断元素是否存在

boolean mightExist = bloomFilter.contains(element1);

System.out.println("元素 " + element1 + " 可能存在: " + mightExist);

String element2 = "element2";

boolean mightExist2 = bloomFilter.contains(element2);

System.out.println("元素 " + element2 + " 可能存在: " + mightExist2);

其中 Google Guava BloomFilter 和 Hutool 框架 BitMapBloomFilter 为单机版的布隆过滤器实现，不适用分布式环境。分布式环境要使用 Redisson 框架中的 RBloomFilter 来实现布隆过滤器，因为它的数据是保存在 Redis 中间件的，而中间件天生支持分布式系统。

小结

位数组和布隆过滤器的区别如下：

位数组：没有误判，但空间利用率低。
布隆过滤器：空间利用率高，但存在对已经存在的数据的误判（不存在的数据没有误判）。

因此，如果对精准度要求高可以使用位数组；如果对空间要求苛刻，可以考虑布隆过滤器。

本文已收录到我的面试小站 www.javacn.site，其中包含的内容有：场景题、并发编程、MySQL、Redis、Spring、Spring MVC、Spring Boot、Spring Cloud、MyBatis、JVM、设计模式、消息队列等模块。