Verilog5_有限状态机

一、有限状态机（Finite State Machine, FSM）基本概念

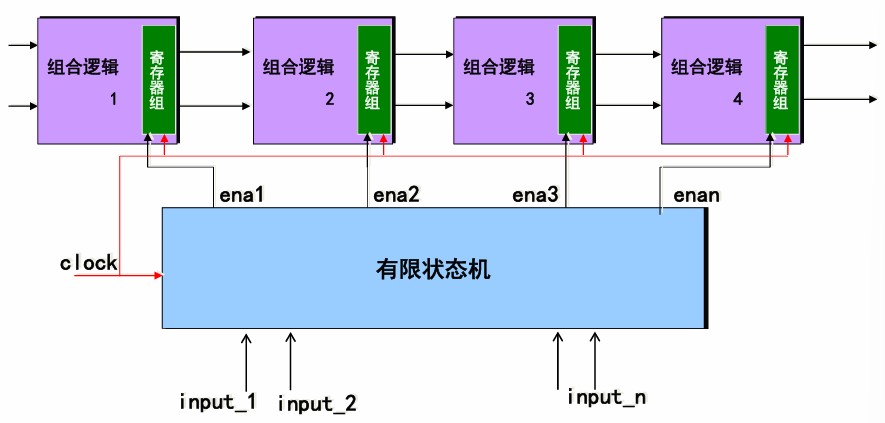
有限状态机是由寄存器组和组合逻辑构成的硬件时序电路；

        其状态只能在同一时钟跳变沿从一个状态转向另一个状态；状态的选择不仅取决于各个输入值，还取决于当前状态，可用于产生在时钟跳变沿时刻开关的复杂的控制逻辑，是数字逻辑的控制核心

1.有限状态机的优势

• 高效的顺序控制逻辑
  
          克服了纯硬件数字系统顺序方式控制不灵活的缺点，在其运行方式上类似于控制灵活和方便的CPU，是高速高效控制的首选
• 容易利用现成的EDA工具进行优化设计
  
          状态机构建简单，设计方案相对固定，使用HDL综合其可以发挥其强大的优化功能；
  
          性能良好的综合器都具有许多可控或自动优化状态机的功能
• 稳定性能
  
          状态机容易构成良好的同步时序逻辑模块，可用于解决大规模逻辑电路设计中的竞争和冒险现象
• 高速性能
  
          在高速通信和高速控制方面，状态机更有其巨大的优势，一个状态机的功能类似于CPU的功能
• 高可靠性能
  
          状态机是由纯硬件电路构成，不存在CPU运行软件过程中许多固有的缺陷；
  
          状态机的设计中能够使用各种容错技术；
  
          当状态机进入非法状态并从中跳出进入正常状态的时间短暂，对系统的危害不大。

2.有限状态机的分类

一般来说，状态机的基本操作主要有：状态机的内部状态转换和产生输出信号序列

        根据电路的输出信号是否与电路的输入有关，可以将状态机划分为：Moore型状态机（输出只与当前电路状态有关，保持输出的稳定性和可预测性）；Mealy型状态机（输出与当前电路状态和当前电路输入有关，来快速响应输入变化）

3.有限状态机的描述方法

• 状态转移图：紧凑，适合描述较为简单的系统

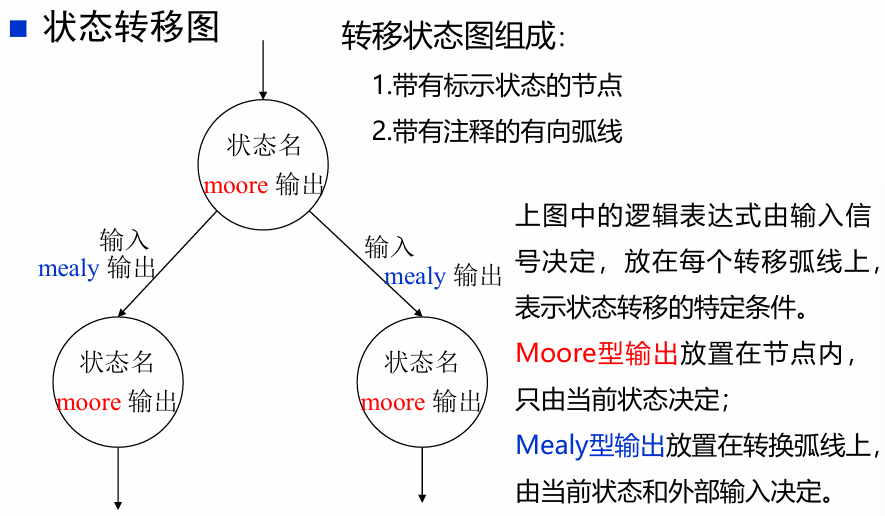
• 算法状态机（ASM）图
  
  算法状态机图更像是流程图，能较好地描述复杂系统中状态的转换和动作

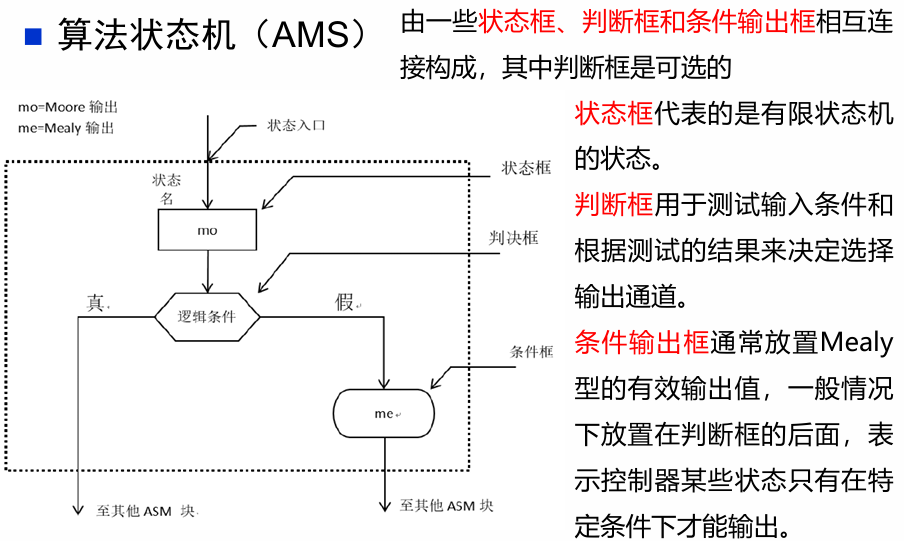
        这两种表示方法包含了相同的信息，都包含了状态机的输入、输出、状态和转换。

二、有限状态机的设计

1.状态机的设计步骤

• 依据具体的设计原则，确定采用Moore型状态机还是Mealy型状态机
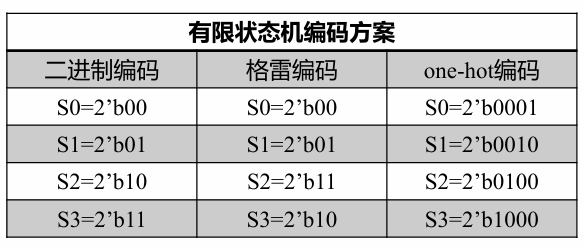
• 分析设计要求，列出状态机的所有状态，并对每一个状态进行状态编码
• 依据状态转移关系和输出函数，画出状态图
• 依据所画的状态图，采用硬件描述语言对状态机进行描述

2.状态图的完备性和互斥性检查

• 完备性： 对于每一个状态，将所有脱离这一状态的条件表达式进行逻辑或运算，如果结果为1就是完备的，否则不完备，也就是说状态图进入某状态后，却不能跳出该状态；
• 互斥性： 对于每一个状态，将所有脱离这一状态的条件表达式找出，然后任意两个表达式进行逻辑与运算，如果结果为0就是互斥的。也就是要保证在任何时候不会激活两个脱离状态的转换，即从一个状态跳到两个状态

3.安全状态机设计

• 状态引导法：对于未使用的状态，也给予次态赋值，避免状态机处于未知状态；
• 状态编码检测法：判断被触发的触发器的个数，当数量大于1时，说明出现问题；
• 借助EDA工具自动生成安全状态机

三、有限状态机的Verilog HDL描述

考虑如下图所示的状态转移图

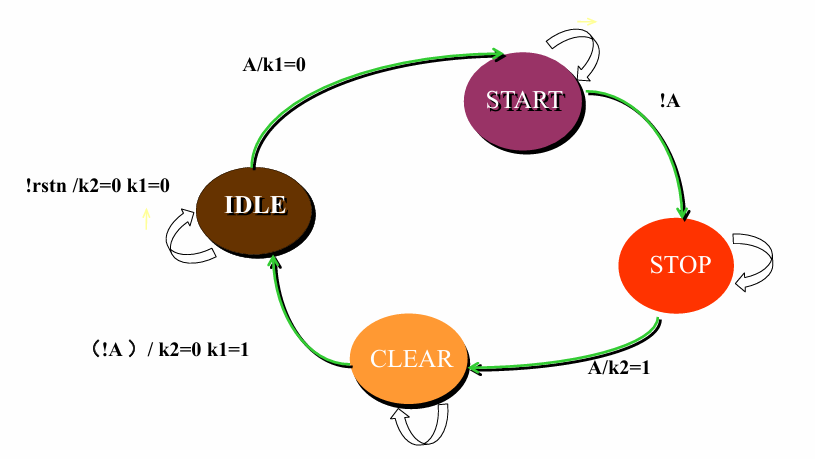
1.描述状态机中各个状态的名称，并指定状态编码

• 状态定义/声明与编码
  • 状态必须是常量parameter或者 `define

    IDLE=2'b00;
    START=2'b01;
    STOP=2'b10;
    CLEAR=2'B11;

• 状态寄存器（位宽必须与parameter变量一致）

  • cur_state:存储现态
  • next_state:存储次态
  • reg [1:0] state:定义状态寄存器

• 状态编码

  

module fsm
	#(parameter IDLE=2'b00,
	  parameter START=2'b01,
	  parameter STOP=2'b10,
	  parameter CLEAR=2'b11)
	( input clk, rstn, a,
	  output reg k1, k2);

	reg [1:0] cur_state, next_state;//定义状态寄存器

2.状态机设计

2.1 设计步骤

• 用时序的always块描述状态触发器实现的状态存储；
• 使用敏感表和case语句（或if-else等价语句）描述的状态转换逻辑
• 描述状态机的输出逻辑

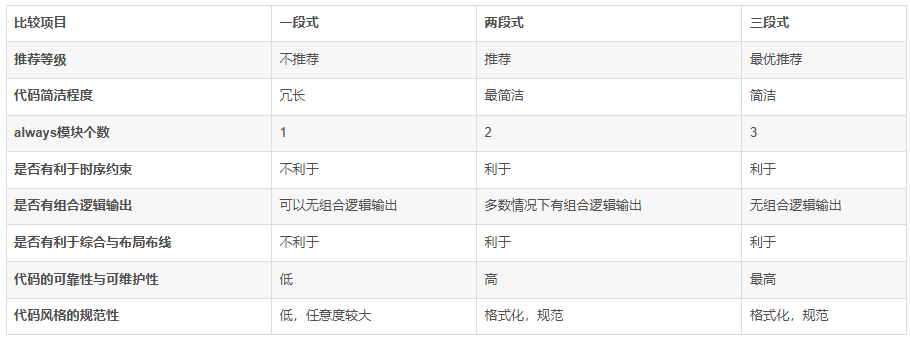
2.2 状态机的三种RTL描述方法

• 一段式：现态、次态与输出逻辑在同一个always块中
• 两段式：现态在一个always块中，次态与输出逻辑在一个always块中
• 三段式：现态、次态与输出逻辑分别在一个always块中

//一段式
always @(posedge clk)	begin
	if(!rstn)	begin
		cur_state<=IDLE;
		k2<=1'b0;
		k1<=1'b0;
	end
	else
		case(cur_state)
			IDLE:
				if(a) begin
					cur_state<=START;
					k1<=1'b0;
				end
				else
					cur_state<=IDLE;
			START:
				if(!a)
					cur_state <= STOP;
				else
					cur_state <=START;
			STOP:
				if(a)	begin
					cur_state <= CLEAR;
					k2<=1'b1;
				end
				else
					cur_state <= STOP;
			CLEAR:
				if(!a)	begin
					cur_state <= IDLE;
					k2<=1'b0;
					k1<=1'b1;
				end
				else
					cur_state <= CLEAR;
		endcase
	end

//两段式
always @(posedge clk)	begin
	if(!rstn)
		cur_state <= IDLE;
	else
		cur_state <= next_state;
end

always @(cur_state, a)	begin
	case(cur_state)
		IDLE:
			if(a) begin
				next_state=START;
				k1=1'b0;
			end
			else
				next_state=IDLE;
		START:
			if(!a)
				next_state = STOP;
			else
				next_state =START;
		STOP:
			if(a)	begin
				next_state = CLEAR;
				k2=1'b1;
			end
			else
				next_state = STOP;
		CLEAR:
			if(!a)	begin
				next_state = IDLE;
				k2=1'b0;
				k1=1'b1;
			end
			else
				next_state = CLEAR;
	endcase
end

//三段式
always@(posedge clk)	begin
	if(!rstn)
		cur_state <= IDLE;
	else
		cur_state <= next_state;
end

always@(cur_state, a)	begin
	case(cur_state)
		IDLE:
			if(a)	next_state = START;
			else	next_state = IDLE;
		START:
			if(!a)	next_state = STOP;
			else	next_state = START;
		STOP:
			if(a)	next_state = CLEAR;
			else	next_state = STOP;
		CLEAR:
			if(!a)	next_state = IDLE;
			else	next_state = CLEAR;
	endcase
end

always@(cur_state, a)	begin
	k2=1'b0;
	k1=1'b0;
	if(!rstn)	begin
		k2=1'b0;
		k1=1'b0;
	end
	else	begin
		if(cur_state == CLEAR && !a)
			k1=1'b1;
		else
			k1=1'b0;
		if(cur_state == STOP && a)
			k2=1'b1;
		else
			k2=1'b0;
	end
end

四、有限状态机设计实例

实例1：Moore型序列检测器：

要求描述：

        序列检测器可用于检测一组或多组由二进制码组成的脉冲序列信号，当序列检测器连续收到一组串行二进制码后，如果这组码与检测器中预先设置的码相同，则输出1，否则输出0

        设计一个“1101”的序列检测器，设din为数字码流输入，sout为检出标记输出，高电平表示发现指定序列，低电平表示没有发现指令序列。

Step1.状态定义

• s0:未检测到“1”
• s1:检测到输入序列“1”
• s2:检测到输入序列“11”
• s3:检测到输入序列“110”
• s4:检测到输入序列“1101”
  
          共五个状态，需要声明位宽为3的状态寄存器reg [2:0] cur_state, next_state;

Step2.状态转移表和状态转移图

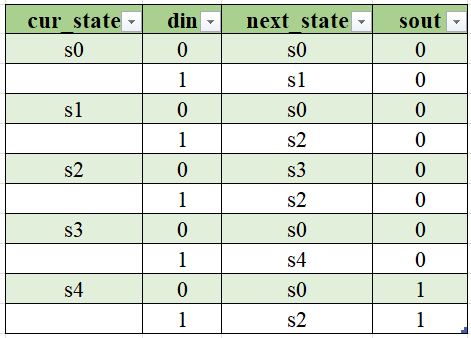
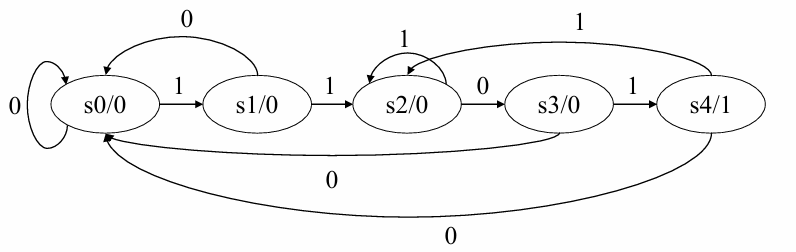
        无可简化状态,对应的Moore型状态转移图如下：

Step3.HDL语言描述状态转换

//实现代码
module seqdet#(
	parameter s0=3'b000,
	parameter s1=3'b001,
	parameter s2=3'b010,
	parameter s3=3'b011,
	parameter s4=3'b100)(
	input clk, rstn, din,
	output reg sout);

	reg [2:0] cur_state, next_state;

	always @(posedge clk)	begin
		if(!rstn)	cur_state <= s0;
		else		cur_state <= next_state;
	end

	always @(cur_state, din)	begin
		sout=0;
		case(cur_state)
			s0:	begin
				if(din == 1)	next_state=s1;
				else		next_state=s0;
			end
			s1:	begin
				if(din == 1)	next_state=s2;
				else		next_state=s0;
			end
			s2:	begin
				if(din == 0)	next_state=s3;
				else		next_state=s2;
			end
			s3:	begin
				if(din == 1)	next_state=s4;
				else		next_state=s0;
			end
			s4:	begin
				if(din == 0)	begin	next_state=s0; sout=1;	end
				else		begin	next_state=s1; sout=1;	end
			end
			default	next_state=s0;
		endcase
	end
endmodule

//仿真代码
module seqdet_tb();
	reg clk, rstn, din;
	wire sout;

	seqdet U1(clk, rstn, din, sout);
	always #1 clk=~clk;

	initial begin
		clk=0; rstn=0; din=0;
		#5 rstn=1;
		#2 din=1;
		#2 din=1;
		#2 din=0;
		#2 din=1;
		#2 din=1;
		#2 din=0;
		#2 din=0;
		#3 rstn=0;
		#5 $finish;
	end
endmodule

仿真得到的波形图如下：

        综合出的电路结构图如下：

        电路状态转移图如下：

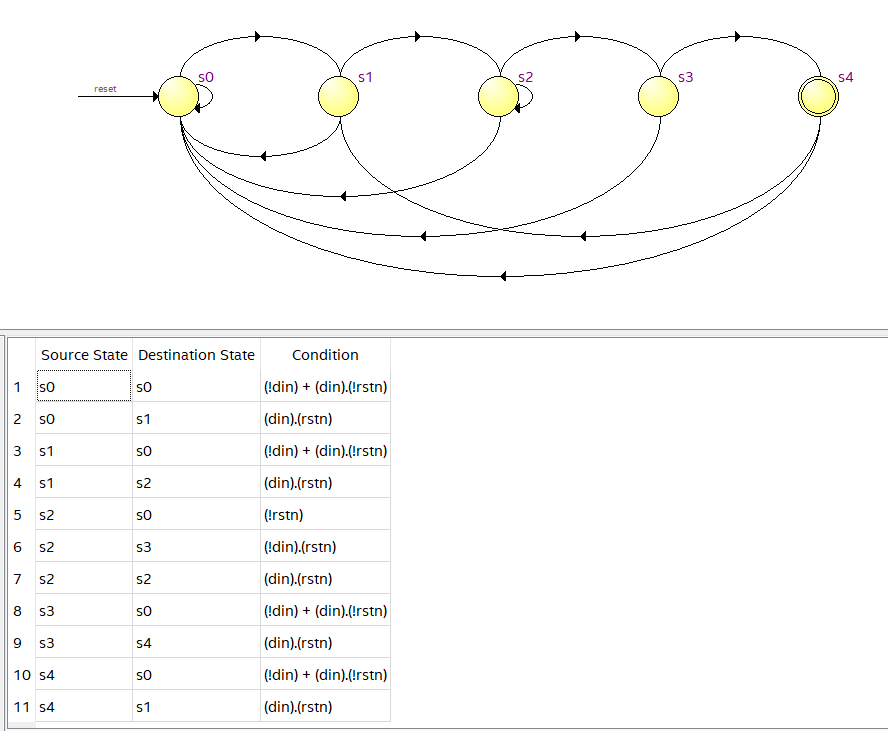
实例2：Mealy型序列检测器：

Step2.状态转移表和状态转换图

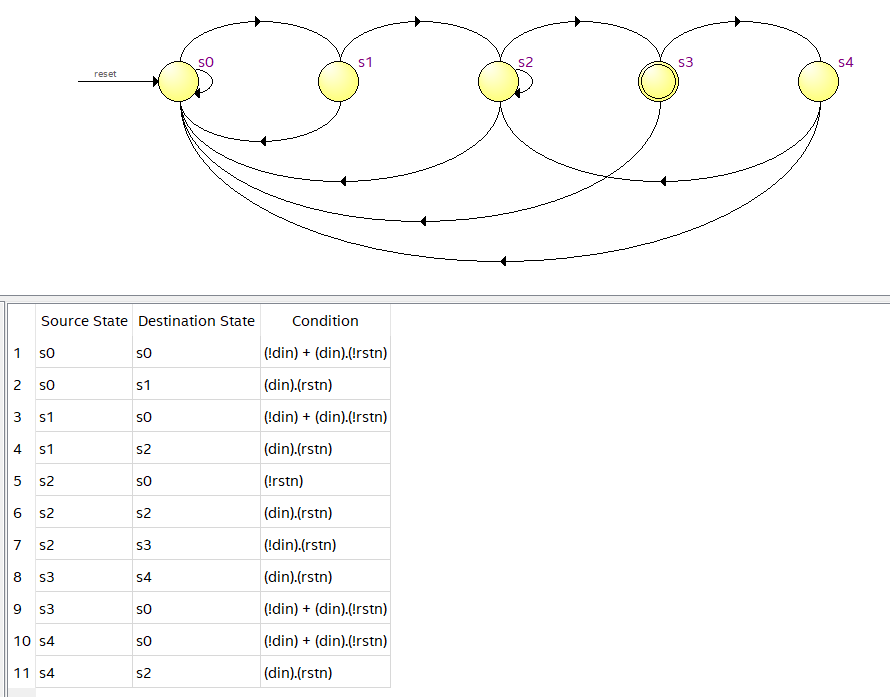
状态定义与实例1相同，可以得到状态转移表如下：

        对应的Mealy型状态转换图如下：

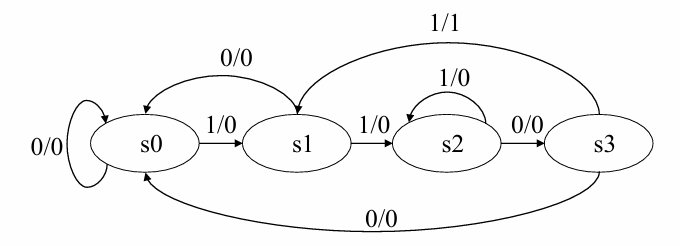
//实现代码
module seqdet_mealy#(
	parameter s0=3'b000,
	parameter s1=3'b001,
	parameter s2=3'b010,
	parameter s3=3'b011,
	parameter s4=3'b100)(
	input clk, rstn, din,
	output reg sout);

	reg [2:0] cur_state, next_state;

	always @(posedge clk)	begin
		if(!rstn)	cur_state <= s0;
		else		cur_state <= next_state;
	end

	always @(cur_state, din)	begin
		sout = 1'b0;
		case(cur_state)
			s0:	if(din==1)	next_state=s1;
				else		next_state=s0;
			s1:	if(din==1)	next_state=s2;
				else		next_state=s0;
			s2:	if(din==0)	next_state=s3;
				else		next_state=s2;
			s3:	if(din==1)	begin	next_state=s4; sout=1;	end
				else		next_state=s0;
			s4:	if(din==1)	next_state=s2;
				else		next_state=s0;
			default:		next_state=s0;
		endcase
	end
endmodule

//仿真代码
module seqdet_mealy_tb();
	reg clk, rstn, din;
	wire sout;

	seqdet_mealy U1(clk, rstn, din, sout);
	always #1 clk=~clk;

	initial begin
		clk=0; rstn=0; din=0;
		#5 rstn=1;
		#2 din=1;
		#2 din=1;
		#2 din=0;
		#2 din=1;
		#2 din=1;
		#2 din=0;
		#2 din=0;
		#3 rstn=0;
		#5 $finish;
	end
endmodule

仿真得到的波形图如下：

        综合出的电路结构图如下：


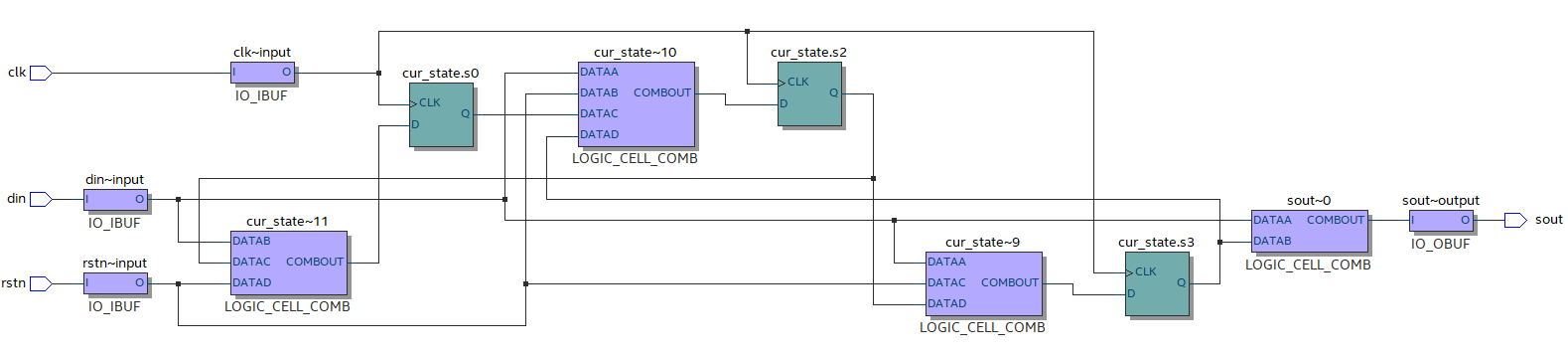
        电路状态转移图如下：