第99：真正理解拉格朗日乘子法和 KKT 条件的更多相关文章

  1. 真正理解拉格朗日乘子法和 KKT 条件

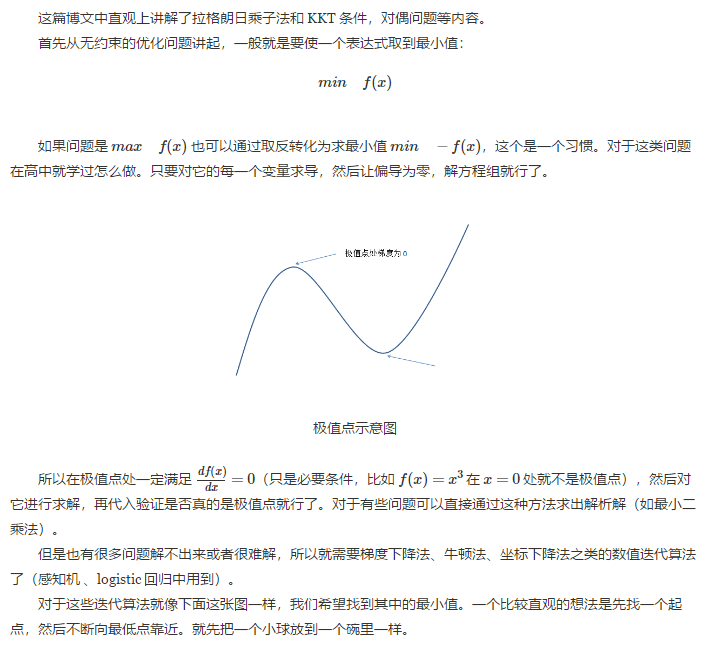
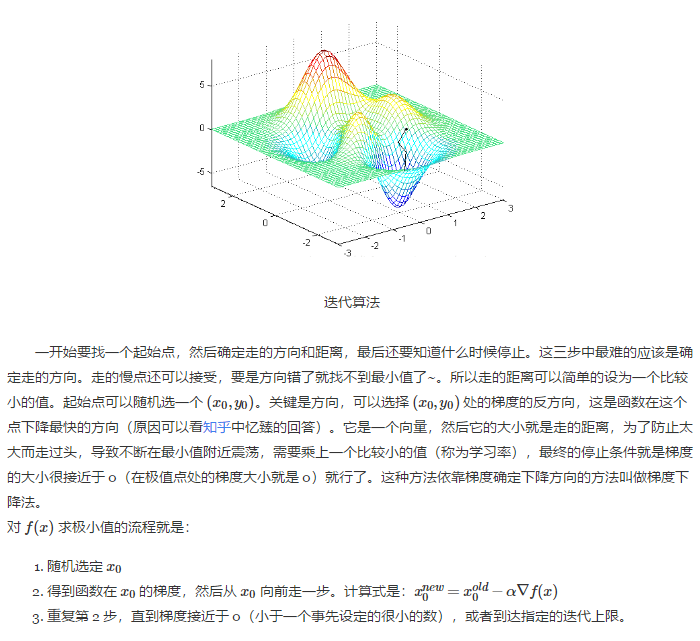
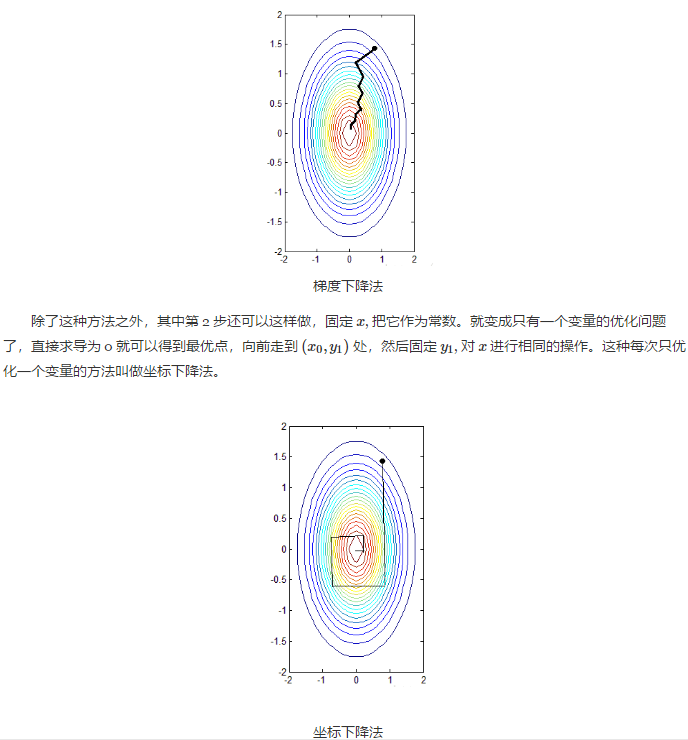
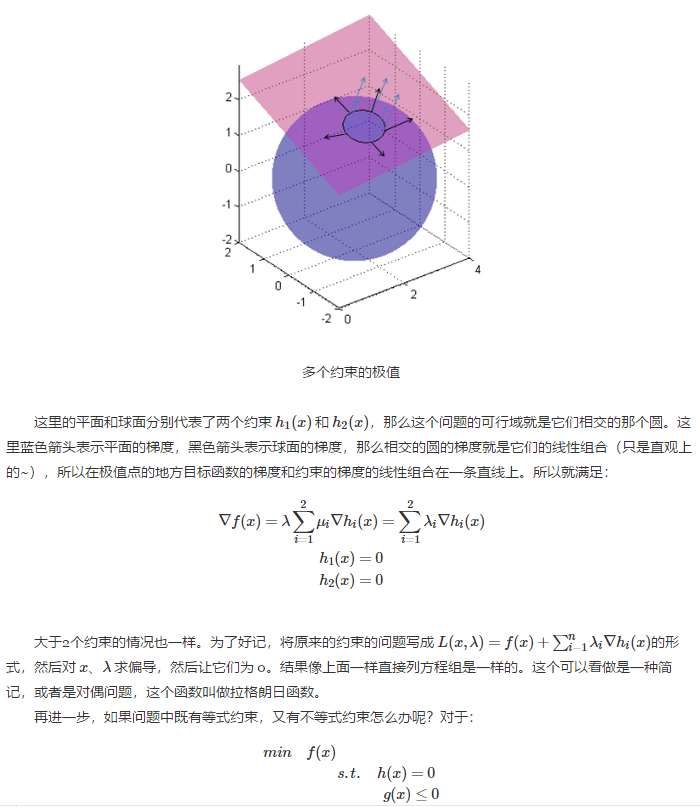
        这篇博文中直观上讲解了拉格朗日乘子法和 KKT 条件,对偶问题等内容.     首先从无约束的优化问题讲起,一般就是要使一个表达式取到最小值: \[min \quad f(x)\]     如 ...

  2. 关于拉格朗日乘子法和KKT条件

    解密SVM系列(一):关于拉格朗日乘子法和KKT条件 标签: svm算法支持向量机 2015-08-17 18:53 1214人阅读 评论(0) 收藏 举报  分类: 模式识别&机器学习(42 ...

  3. 机器学习笔记——拉格朗日乘子法和KKT条件

    拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题.在介绍拉格朗日乘子法之前,先简要的介绍一些 ...

  4. 重温拉格朗日乘子法和KKT条件

    在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值:如果含有不等式 ...

  5. 拉格朗日乘子法和KKT条件

    拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件 ...

  6. 拉格朗日乘子法 - KKT条件 - 对偶问题

    接下来准备写支持向量机,然而支持向量机和其他算法相比牵涉较多的数学知识,其中首当其冲的就是标题中的拉格朗日乘子法.KKT条件和对偶问题,所以本篇先作个铺垫. 大部分机器学习算法最后都可归结为最优化问题 ...

  7. 拉格朗日乘子法&KKT条件

    朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件.前 ...

  8. 【整理】深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有不等约束时使用 ...

  9. 深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    [整理]   在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有 ...

随机推荐

  1. C++入门经典-例3.1-判断输入的数字是否为奇数

    1:代码如下: // 3.1.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <iostream> using ...

  2. Docker入门-数据挂载

    Docker数据管理 在容器中管理数据主要有两种方式: 数据卷(Volumes) 挂载主机目录(Bind mounts) 数据卷 数据卷是一个可供一个或多个容器使用的特殊目录,它绕过UFS,可以提供很 ...

  3. gdb调试时忽略SIGPIPE 等信号

    GDB调试网络程序时,会遇到SIGPIPE信息,默认GDB会把程序停下来,即使程序使用signal(SIGPIPE, SIG_IGN);来忽略信号.用handle命令设置一下缺省的signal的处理行 ...

  4. img控件的居中显示 ---js技术

    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...

  5. leetcode-easy-trees-102. Binary Tree Level Order Traversal-YES

    mycode  98.56% # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x ...

  6. cinder-----常用命令

    云硬盘的创建查询 #创建卷类型 cinder type-create rbd #rbd是云硬盘类型名称,可自行定义 #查询卷类型 cinder type-list #卷类型扩展规格 cinder ty ...

  7. Dojo入门：dojo中的事件处理

      JS为DOM添加事件 在原生的环境下,为DOM添加事件处理函数有多种方法: <input type="button" name="btn" value ...

  8. java：maven（maven-ssm（聚合，分包开发））

    1.maven-ssm: maven-ssm_diy: pom.xml: <?xml version="1.0" encoding="UTF-8"?> ...

  9. 彻底搞懂snowflake算法及百度美团的最佳实践

    写在前面的话 一提到分布式ID自动生成方案,大家肯定都非常熟悉,并且立即能说出自家拿手的几种方案,确实,ID作为系统数据的重要标识,重要性不言而喻,而各种方案也是历经多代优化,请允许我用这个视角对分布 ...

  10. P3367 【模板】并查集

    喵呜~~(题面) 这题其实很早就过了,但是呢,以前过的时候真的基本上是CtrlC+CtrlV,这次把代码重新码了一遍,对并查集也有了一个基本清晰的认识 #include<iostream> ...