P2158仪仗队

今天早上你谷崩了

由于脑子抽筋，所以选了一道数学题来做。做着做着就疯了

传送

窝盟先画张图冷静冷静

这是样例的图，其中蓝点是有学生的地方。

窝盟来看一下那些学生可以被C君看到。

假设这张图是一个坐标系，C君在(0,0)。

C君可以看到的学生：(1,0),(0,1),(1,1),(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)

我们画下来（下图中红点是可以看到的学生）

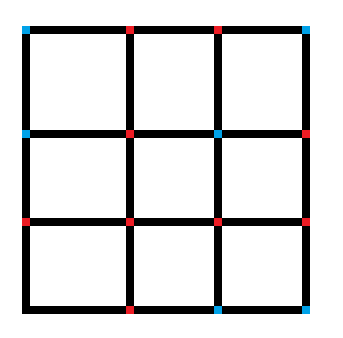
我们发现红点的横纵坐标的最大公约数都是1，且所有红点关于y=x对称。

所以我们可以求出来一半的红点，再*2-1（因为(1,1)关于y=x对称后还是(1,1),所以要-1）

我们再看一下数据范围：

显然O(n²)枚举横纵坐标会TLE。

我们发现对于合法的点(i,j)来说，gcd(i,j)=1,也就是说i与j互质。所以我们要找出所有符合(i,j)互质的二元组(i,j)。

仔细思考，想起有一个神奇的函数，叫欧拉函数。φ(n)是求从1到n-1中，有多少个与n互质的数。

为了不重复，不少求符合条件的(i,j),我们求出1到n-1这些数的φ，然后乘2.

似乎少求了什么东西。是什么呢？是什么呢？是什么呢？

我们好像忽略了(1,0)和(0,1)这两个点，还把(1,1)算了两遍

那就在当前答案上直接+1好了

怎么快速求φ？

我们先看几个式子：

若n,m互质，φ(nm)=φ(n)φ(m)

p为质数，φ(p)=p-1;

通向公式：φ(n)=n(1-1/p1)(1-1/p2).....(1-1/pk)  (其中p1,p2...pk为n的所有质因子)

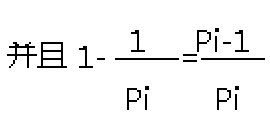
所以φ(n)=n/pi*(pi-1) (1<=i<=k)

以下是求φ的代码：

int phi(int k)
{
    if(k==)return ;
    if(!no[k])return k-;
    cn=;
    int p=k,h=k;
    for(int i=;i*i<=k;i++)
    {
        if(h%i==)
         {
             p=p/i*(i-);//上面的推导
             h/=i;
             while(h%i==)
              h/=i;//我们只用到不同的质因数
         }

    }
    if(h>) p=p/h*(h-);//如果此时的h是最后一个质因数，还要更新p
    return p;
}

但是有一个特殊情况：n=1。

按照我们的思路，最后答案会是1，因为在n≠1时，加上了(1,0),(0,1)，减去了多余的(1,1),所以答案+1，但是当n=1时，只有C君，没有学生，所以答案是0.

本题代码

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define ll long long
using namespace std;
int n,pre[],cnt,all,cn,ys[];
bool no[];
int read()
{
    char ch=getchar();
    int x=;bool f;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return f?-x:x;
}
int phi(int k)
{
    if(k==)return ;
    if(!no[k])return k-;
    cn=;
    int p=k,h=k;
    for(int i=;i*i<=k;i++)
    {
        if(h%i==)
         {
             p=p/i*(i-);
             h/=i;
             while(h%i==)
              h/=i;
         }

    }
    if(h>) p=p/h*(h-);
    return p;
}
int main()
{
   n=read();
   if(n==)//注意特判
   {
       printf("");return ;
   }
   all=;
   for(int i=;i<=n;i++)
    {
        if(!no[i])
            pre[++cnt]=i;
        for(int j=;j<=cnt;j++)
        {
            if(i*pre[j]>n)break;
            no[i*pre[j]]=;
            if(i%pre[j]==)
            break;
        }
    }
    no[]=;
    for(int i=;i<=n-;i++)
    {
         all+=phi(i);
    }
   all*=;
   all+=;
   printf("%d",all);
}