Markov Decision Process in Detail

From the last post about MDP, we know the environment consists of 5 basic elements:

S:State Space of environment;

A:Actions Space that the environment allows;

{P_s,s'}:Transition Matrix, the probabilities of how environment state transit from one to another when actions are taken. The number of matrices equals to the number of actions.

R: Reward, when the system transitions from state s to s' due to action a, how much reward can an agent receive from the environment. Sometimes, reward have different definition.

γ: How reward discounts by time.

How Different between MDP and MRP:

Keyword: Action

The five elements of MDP can be illustrated by the chart below, in which the green circles are states, orange circles are actions, and there are two rewards. In MRP and Markov Process, we directly know the transition matrix. However, in the transition path from one state to another is interupted by actions. And it's worth noting that when the environment is at a certain state, there is no probabilities for actions. The reason is quite understandable: we live in the some world(environment), but different people have different behaviors.

Agent and Policy

Agent is the person or robot who interacts with the environment in Reinforcement Learning. Like human being, everyone may have different behavior under the same condition. The probability distribution of behaviors under different states is Policy. There are so many probabilities in an environment, but for a specific agent (person), he or she may take only one or several possible actions under a certain state. Given states, the policy is defined by:

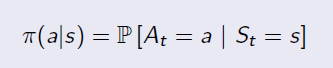
An example of policy is shown below:

From MRP to MDP: MRP+Policy

Transition Matrix: Without policies we do not exactly know the the probability from state s transitioning to s', because different agents may have different probabilitie to take actions. As long as we get π, we can calculate the state transition matrix.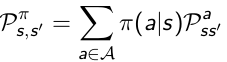

In the chart above, for example, if an agent has probabilitie 0.4 and 0.6 for action a0 and a1, the transition probability from s0 to s1 is: 0.4*0.5+0.6*1=0.8

Reward:

In MDP the reward function is related to actions, which average the uncertainties of the result from an action.

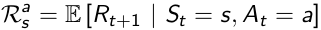
Once we've got the Policy π, we know the action distribution of a specific agent, so we can average the uncertaintie of actions, then measure how much immediate reward can receive from state s under policy π.

So now we go back from MDP to MRP, and the Markov Reward Process is defined by the tuple

 

Two Value Functions:

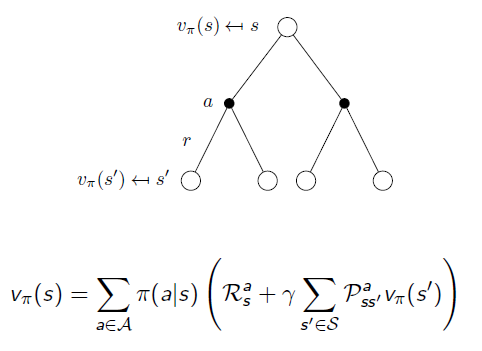
State Value Function:

State Value Function is the same as the value function in MRP. It is used to evaluate the goodness of being in a state s(by immedate and future reward), and the only difference is to average the uncertainty of actions under policy π. It is in the form of:

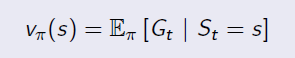
Action Value Function:

To average uncertainties of actions, it's neccesary to know the expected reward from possible actions. So we have Action Value Functionin MDP, which reveals whether an action is good or bad when an agent takes an particular action in state s.

If we calculate expectation of Action Value Functions under the same state s, we will end up with the State Value Function v:

Similarly, when an action is taken, the system may end up with different states. When we remove the uncertainty of state transition, we go back from State Value Function to Action Value Function:

If we put them together:

Another way: