python语言绘图：绘制一组以beta分布为先验，以二项分布为似然的贝叶斯后验分布图

代码源自:

https://github.com/PacktPublishing/Bayesian-Analysis-with-Python

===========================================================

本图可能稍微复杂一些，故给出一些说明。

由贝叶斯定理可知，先验分布乘以似然分布便得到后延分布。由于beta分布为二项分布的共轭先验，也就是说以beta分布为先验，以二项分布为似然分布，所得到的后验分布依然是一种beta分布。

具体的公式说明参见书《Bayesian Analysis with Python》。

代码：

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
palette = 'muted'
sns.set_palette(palette); sns.set_color_codes(palette)
 
theta_real = 0.35
trials = [0, 1, 2, 3, 4, 8, 16, 32, 50, 150]
data = [0, 1, 1, 1, 1, 4, 6, 9, 13, 48]
 
beta_params = [(1, 1), (0.5, 0.5), (20, 20)]
dist = stats.beta
x = np.linspace(0, 1, 100)
 
for idx, N in enumerate(trials):
    if idx == 0:
        plt.subplot(4,3, 2)
    else:
        plt.subplot(4,3, idx+3)
    y = data[idx]
    for (a_prior, b_prior), c in zip(beta_params, ('b', 'r', 'g')):
        p_theta_given_y = dist.pdf(x, a_prior + y, b_prior + N - y)
        plt.plot(x, p_theta_given_y, c)
        plt.fill_between(x, 0, p_theta_given_y, color=c, alpha=0.6)
 
    plt.axvline(theta_real, ymax=0.3, color='k')
    plt.plot(0, 0, label="{:d} experiments\n{:d} heads".format(N, y), alpha=0)
    plt.xlim(0,1)
    plt.ylim(0,12)
    plt.xlabel(r"$\theta$")
    plt.legend()
    plt.gca().axes.get_yaxis().set_visible(False)
plt.tight_layout()
plt.savefig('B04958_01_05.png', dpi=300, figsize=(5.5, 5.5))
 
plt.show()

该部分代码意思是判断一个硬币投掷后正面朝上的概率为多少。当然如果一个硬币制作时如果保证质量均匀肯定是正面朝上的概率为0.5，但是如果硬币的质量不是均匀的那么情况就不一定了，这里的背景就是如此。

如果投掷后正面100%朝上则记概率为1，如果正面100%朝向则记概率为0，本文代码中假设正面朝上的概率为0.35，也就是theta_real = 0.35，也就意味着投掷100次会有35次正面朝上。

代码中的

beta_params = [(1, 1), (0.5, 0.5), (20, 20)]

里面的每一个元组代表着一种beta先验分布中的α和β，比如（1,1）则代表着一种beta先验分布中α=1和β=1。

代码中的

trials = [0, 1, 2, 3, 4, 8, 16, 32, 50, 150]
data = [0, 1, 1, 1, 1, 4, 6, 9, 13, 48]

代表着二项分布实验的样本数据，trials意味着投掷硬币的次数，data代表着硬币正面朝上的次数，在这里该二项分布作为似然分布。

用贝叶斯的思想来解释，就是说在投掷实验开始之前我们有一个先验，也就是有个主观的猜测，这个猜测硬币正面朝上的概率其概率本身作为beta分布中的自变量，也就是说先验假设正面朝上的概率服从beta分布，而beta分布中的自变量本身取值范围为0到1，也就是说beta分布是概率的概率分布。

先验分布用beta分布表示，似然分布则服从二项分布，这样先验概率乘以似然概率便能得到后验概率，这里的后验概率仍为一种beta分布。

绘图：

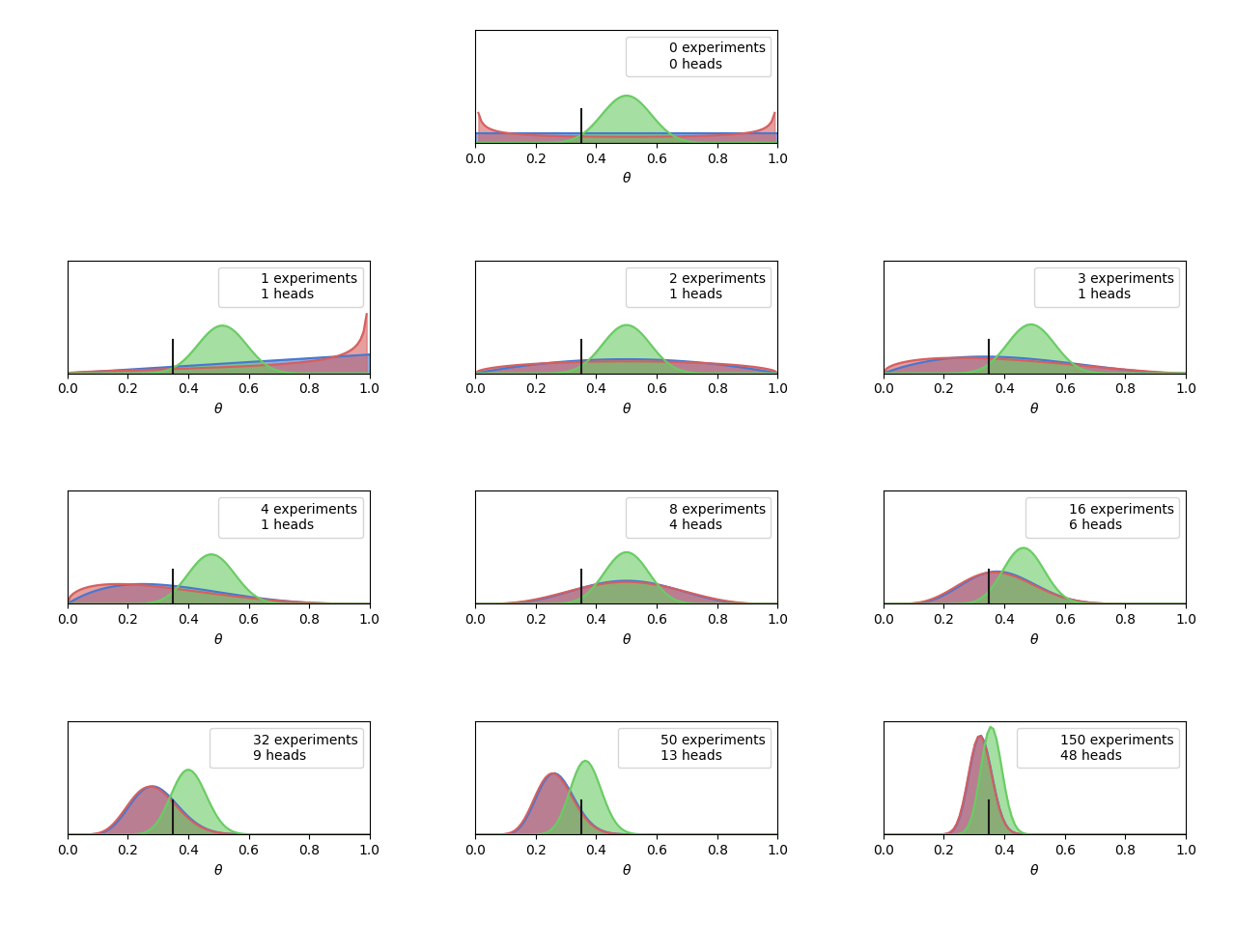
从上面的绘图结果可以看出，在试验次数（投掷次数）较少的情况下先验概率的好坏对后验概率的影响最大，也就是说在试验次数（投掷次数）（似然概率相同的情况）较少的情况下好的假设（好的先验）所得到的后验概率要比坏的假设（坏的先验）所得到的后验概率要好的多；但是随着试验次数（投掷次数）的增加先验对后延的影响逐渐减小，如果试验次数（投掷次数）增加到一定程度后不同的先验对后验的影响可以小到忽略。

由于先验使用的是beta分布，似然为二项分布，所以得到的后验仍为beta分布，根据贝叶斯定理的计算可以知道单次试验后所得到的后验分布作为下次试验的先验分布这样依次累积到总的试验次数所得到的最终后验分布等于用最初的先验分布与总的试验所得的二项分布的样本数据所得到的后验分布。而之所以这里有这种单次计算累积等效于总的试验数据一次计算是因为我们这里的先验分布采用的假设为beta分布，而似然分布也就是采样的的数据服从二项分布，而beta分布与二项分布为共轭分布，因此才有这样的性质。

根据：https://www.cnblogs.com/devilmaycry812839668/p/16358979.html可知，

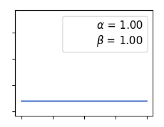
α=1和β=1时beta分布为均匀分布，也就是说在该种假设先验的情况下假设的是硬币正面朝上的概率服从均匀分布，也就是说先验假设硬币正面朝上的各概率取值的概率是相当的，也就是说此时假设硬币正面朝上概率为0，为0.1, 0.2，...... ，0.9， 1.0 的概率均相同。

α=1和β=1时beta分布为均匀分布，此时根据信息熵理论可知此时的先验假设是没有任何信息量的，因为均匀分布就是一种信息混杂是不具备信息量的。由此可知上图中蓝色的曲线可以看做更加贴近频率统计学的表现，也就是说蓝色曲线表示的后验分布的期望正好等于频率统计中的样本期望值。

===========================================================